백준 2167번 2차원 배열의 합 (Python, DP)

백준 2167번 2차원 배열의 합 문제 바로가기

문제 이해

문제

2차원 배열이 주어졌을 때 (i, j) 위치부터 (x, y) 위치까지에 저장되어 있는 수들의 합을 구하는 프로그램을 작성하시오. 배열의 (i, j) 위치는 i행 j열을 나타낸다.

입력

첫째 줄에 배열의 크기 N, M(1 ≤ N, M ≤ 300)이 주어진다. 다음 N개의 줄에는 M개의 정수로 배열이 주어진다. 배열에 포함되어 있는 수는 절댓값이 10,000보다 작거나 같은 정수이다. 그 다음 줄에는 합을 구할 부분의 개수 K(1 ≤ K ≤ 10,000)가 주어진다. 다음 K개의 줄에는 네 개의 정수로 i, j, x, y가 주어진다(1 ≤ i ≤ x ≤ N, 1 ≤ j ≤ y ≤ M).

출력

K개의 줄에 순서대로 배열의 합을 출력한다. 배열의 합은 231-1보다 작거나 같다.

문제 접근

for문으로 시작점과 끝점까지의 합을 매 명령마다 더할 수도 있지만, 그렇게 되면 너무 오래걸리는 문제가 발생한다!
따라서 dp테이블을 만들어 합을 저장하여 단순계산을 통해 명령을 수행할 수 있을 것이다.
개인적으로 그림을 그려서 생각해보는 것이 되게 도움이 많이 될 것 같았다.

• DP테이블 구성하기
• 출력 값 계산하기

문제 풀이

DP테이블 구성하기

DP테이블은 단순하게 생각하면 0,0부터 x,y까지의 합을 저장하면 된다!
아래는 점화식이다.

dp[x][y] = dp[x-1][y] + dp[x][y-1] - dp[x-1][y-1] + arr[x][y]

위의 점화식을 보면 x,y까지의 합은 x-1,y까지의 합을 더하고 x,y-1까지의 합을 더하고 x-1,y-1까지의 합을 빼주고 arr[x][y]를 더한것이라고 볼 수 있다.

arr[x][y]는 x,y의 값이니까 당연히 더해줘야 한다.
x-1,y-1까지의 합을 빼준 이유는 x-1,y까지의 합을 더하고 x,y-1까지의 합을 더하는 과정에서 중복되어 더해줬기 때문에 한번 빼주었다.

그림으로 보면 아래와 같다.

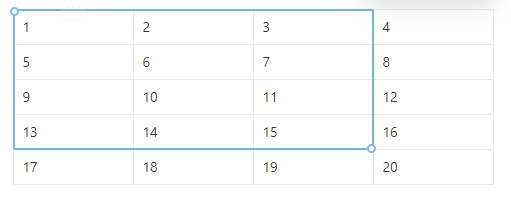
위의 그림과 같은 합을 구하고 싶을 때

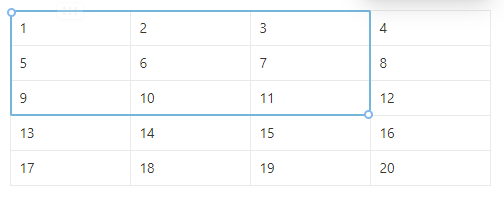
위의 범위와

위의 범위를 더하고

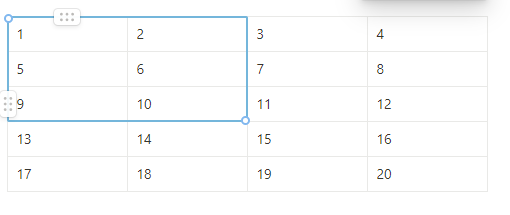
마지막으로 공통된 범위를 빼준 후에 15를 더하면 우리가 구하고자 하는 범위가 나오게된다.

for i in range(1,N+1):
    for j in range(1,M+1):
        dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i-1][j-1] - dp[i-1][j-1]

출력 값 계산하기

do에 우리가 수행해야할 명령들을 담아두었다.
이제 우리는 i,j부터 x,y까지의 합을 구해야 한다.
그 합은 이렇게 생각할 수 있을 것이다.

(0,0부터 x,y까지의 합)에서 (0,0부터 x,j-1까지의 합)을 빼고 (0,0부터 i-1,y까지의 합)을 빼고 두 번 빼준 (0,0부터 i-1,j-1까지의 합)을 다시 더해주면 된다.

for _, line in enumerate(do):
    i,j,x,y = line
    print(dp[x][y]-(dp[x][j-1]+dp[i-1][y])+dp[i-1][j-1])

만약 아래의 사진에서 6이 들어가있는 자리부터 15가 들어가 있는 자리까지의 합이 궁금하다면

우리는 아래의 범위를 구해야 할 것이다.

따라서 아래의 범위에서

아래의 범위를 빼고

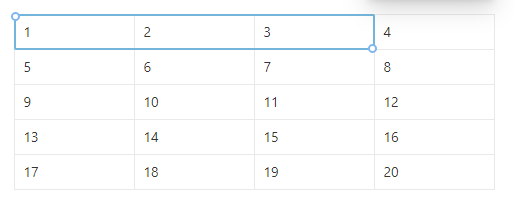
아래의 범위를 빼고!

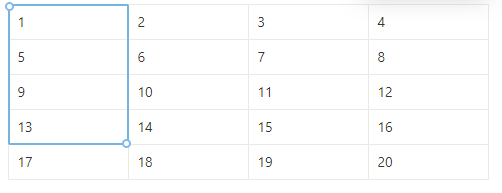
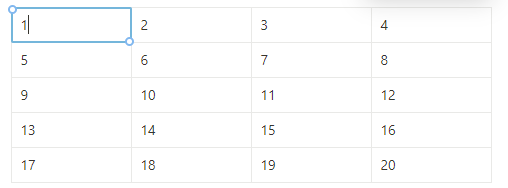
마지막으로 중복으로 빼주었던 부분을 더해주면 된다!

제출 코드

import sys
N, M = map(int, sys.stdin.readline().split())
arr = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
K = int(sys.stdin.readline())
do = [list(map(int, sys.stdin.readline().split())) for _ in range(K)]

dp = [[0 for i in range(M+1)] for _ in range(N+1)]
for i in range(1,N+1):
    for j in range(1,M+1):
        dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i-1][j-1] - dp[i-1][j-1]
for _, line in enumerate(do):
    i,j,x,y = line
    print(dp[x][y]-(dp[x][j-1]+dp[i-1][y])+dp[i-1][j-1])