[ 논문 리뷰 ] Show, Attend and Tell : Neural Image caption Generation with Visual Attention

JSM0315·2025년 3월 29일

논문리뷰

목록 보기

8/24

한마디 정리

Image Caption 모델에서 이미지의 특정 부분을 단어를 예측할 때마다 강조하도록 하는 Attention 매커니즘을 적용한 모델로 모델이 단어를 예측할 떄 이미지의 어느 부분을 보고 단어를 예측하는지에 대한 인사이트를 제공합니다.

Abstract

이전의 객체 탐지와 기계번역 발전을 기반으로, 해당 논문에서는 Attention 기반의 이미지 설명 모델을 제안하고 있습니다. Backpropagation을 통한 학습과 변분 하한을 최대화 하는 방식으로 확률적으로 학습할 수 있는 방법을 제안합니다. 추가로 시각화를 통해서 모델이 출력 시퀀스에서 단어 생성시 자동으로 이미지내 중요한 객체에 시선을 고정함을 보여줍니다.

Introduction

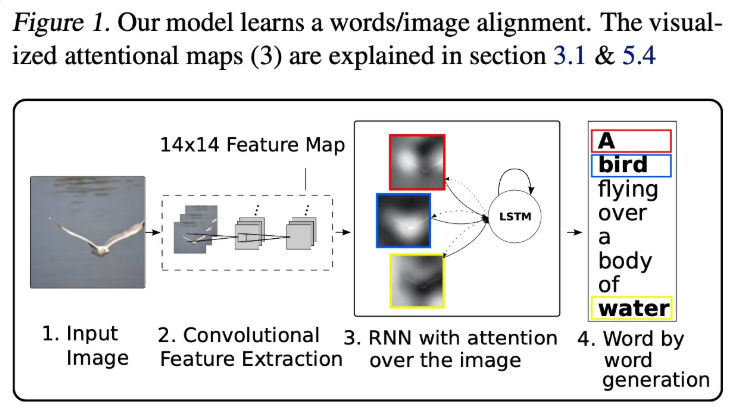
이미지 설명의 경우 이미지 내부에서 객체를 찾은 후 이를 언어로 설명해야 하기 때문에 굉장히 어려운 과제입니다. 하지만 이미지 설명이 자동으로 가능한 경우 복잡한 이미지를 언어로 압축하여 저장할 수 있다는 큰 장점을 가지고 있습니다. 그리고 최근 CNN의 발전과 RNN의 발전으로 이 둘을 결합하여 이미지 설명 모델이 발전을 이루고 있습니다.

인간 시각 시스템 중에서 매우 흥미로운 특징은 “Attention”이 존재한다는 것입니다. 이미지를 받아 들일때 전체 이미지를 하나의 특징으로 압축하는 것이 아니라, 상황에 따라서 동적으로 특징이 도드라지도록 유도합니다. 기존의 연구에서는 CNN의 high dimention feature map만을 사용하여 이미지 내에서 가장 잘 도드라지는 특징만 사용한 반편, attention을 활용하게 되면 보다 low level의 feature map을 사용하여 여러 표현력을 유지할 수 있게 됩니다.

그래서 해당 논문에서는 이미지 설명 모델에 Attention 매커니즘을 도입합니다. 이때 2가지 접근 방식을 소개하고 있습니다.

Hard attention : 특정 위치에 선택적으로 집중할 수 있도록 유도합니다.
Soft attention : 확률 분포 전체에 부드럽게 집중 할 수 있도록 유도합니다.

attention 매커니즘을 적용하게 되면 모델이 이미지의 어느 부분을 보고 단어를 출력했는지를 시각적으로 알 수 있다는 장점을 가지고 있습니다.

각 단어에 대해 attention으로 관심 영역이 강조되지만, A, over등의 단어가 유의미한 결과인지는 의구심이 든다.

해당 논문은 다음과 같은 방법을 통해서 아래와 같이 3가지 부분에 기여를 하고 있습니다.

Attention을 도입한 이미지 캡션 모델 제안
시각화를 통한 해석 가능성 제공
여러 데이터셋에 대한 SOTA 달성

Image caption Generation with Attention Mechanism

Model Detail

해당 논문에서는 2가지 변형된 ( soft, hard) 를 제않고 있기에, 우선 둘의 공통적인 Framwork를 소개하고 있습니다.

Encoder: Convolutional features

단어의 경우 모드 원핫인코딩 처리를 진행하게 되어 만일 사용하는 단어의 수가 K개인 경우 각각의 단어는 K 차원으로 임베딩 됩니다. 그리고 이미지의 설명 문장의 길이가 C인 경우 아래와 같이 표현할 수 있습니다.

y = \{\,\mathbf{y}_1, \dots, \mathbf{y}_C\}, \quad \mathbf{y}_i \in \mathbb{R}^K

추가로 본 논문에서는 이미지를 하나로 압축하는 것이 아니라 단어를 추출할 때 마다 이미지의 어느부분이 강조되는지 알기 위해서 공간별로 총 L개의 벡터를 생성하게 됩니다. 그리고 각각의 벡터는 D차원을 갖게 됩니다. 이를 표현하면 아래와 같습니다.

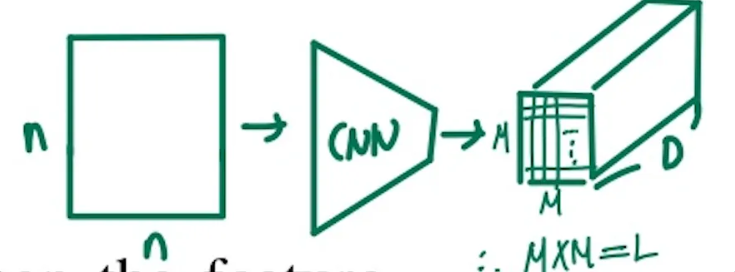
a = \{\,\mathbf{a}_1, \dots, \mathbf{a}_L\}, \quad \mathbf{a}_i \in \mathbb{R}^D

그림으로 간단하게 살펴보면 다음과 같이 표현 해볼 수 있고 M x M 크기의 feature map에서 각각의 cell이 하나의 vector가 된다. 그래서 M x M = L 수식을 만족하게 된다.

Decoder : Long short-term memory network

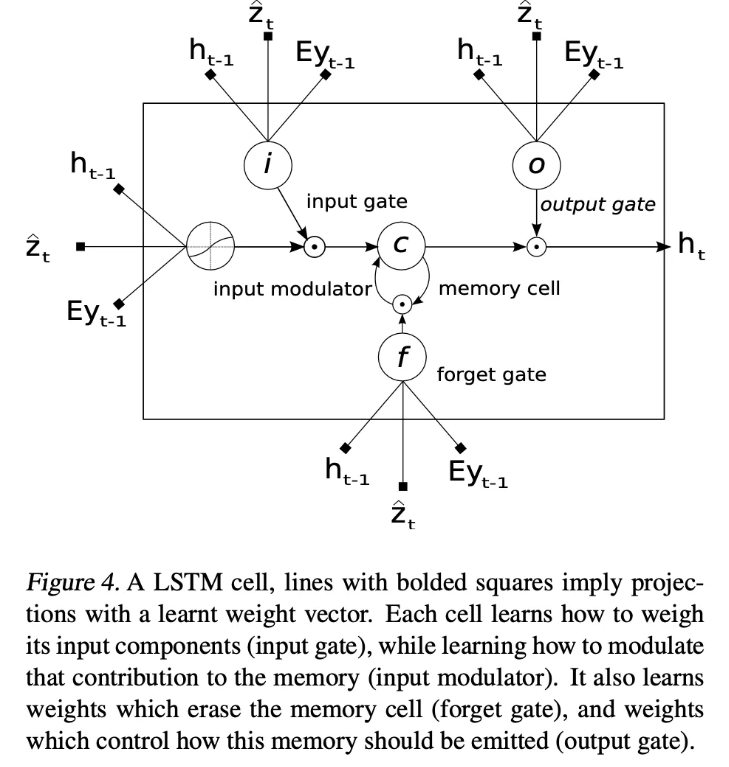
Decoder의 경우 기존의 LSTM의 작동방식에서 이미지에 대한 context vector를 입력으로 넣게 됩니다.

이를 간단하게 수식으로 표현하게 되면 아래와 같이 나타낼 수 있습니다.

\begin{pmatrix} i_t \\ f_t \\ o_t \\ g_t \end{pmatrix} = \begin{pmatrix} \sigma \\ \sigma \\ \sigma \\ \tanh \end{pmatrix} T_{D+m+n,n}\!\Bigl( \begin{pmatrix} E\,y_{t-1} \\ h_{t-1} \\ \hat{z}_t \end{pmatrix} \Bigr)

이는 모든 Gate에 대한 정보를 하나의 행렬로 표현한것이고, 이를 분할 해서 살펴보면 LSTM과 다를게 없습니다. 여기서 우리가 추가로 살펴봐야하는 것은 $\hat{z}_t$ 입니다. 이는 context vecotr이며, 각 t 시간 마다 모델이 참고해야하는 attention정보를 가지고 있습니다. context vector의 경우 additive attention매커니즘을 활용하여 구하게 됩니다.

e_{t,i} = f_{\text{att}}\bigl(a_i;\, h_{t-1}\bigr)

다음과 같이 간단한 MLP인 $f_{att}$ 함수가 존재합니다. 해당 함수의 경우 간단하게 $Result = V^T tanh(h_tW_h + a_tW_a)$ 다음과 같이 매우 간단한 수식을 통해서 특정 scalar 값을 얻게 됩니다.

\alpha_{t,i} = \frac{\exp\bigl(e_{t,i}\bigr)}{\sum_{k=1}^{L}\exp\bigl(e_{t,k}\bigr)}

이후 다음과 같이 softmax를 통해서 각 이미지의 영역 별로 얼마나 중요한지를 확률 값으로 표현하게 됩니다. 그리고 최종적으로 아래와 같은 식을 통해서 context vector를 얻을 수 있게 됩니다. 이러한 과정을 통해서 context vector는 D차원으로 압축이 되게 됩니다.

\hat{z}_t = \phi\!\Bigl(\{a_i\},\, \{\alpha_i\}\Bigr)

그리고 hidden state와 cell state는 annotation vector ( 이미지 L * D 크기의 feature map ) 각각의 영역을 평균하여 초기화 하게 됩니다. 즉 hidden state 와 cell state 모두 이미지 정보에 영향을 받도록 초기화가 진행이 되게 됩니다.

c_0 = f_{\text{init,c}}\!\Bigl(\frac{1}{L}\,\sum_{i=1}^{L} a_i\Bigr) \\ h_0 = f_{\text{init,h}}\!\Bigl(\frac{1}{L}\,\sum_{i=1}^{L} a_i\Bigr)

이후 ( hidden state, context vector, embedding word ) 를 입력으로 받아 다음 단어에 대한 확률 분포를 얻게 됩니다.

p\bigl(y_t \mid a,\; y_{1}^{t-1}\bigr) \;\propto\; \exp\!\Bigl(   L_o\bigl(E\,y_{t-1}\bigr)   \;+\;   L_h\,h_t   \;+\;   L_z\,\hat{z}_t \Bigr)

간단 정리 : t 시간 마다 hidden state와의 addative attention을 통해서 특정 부분을 강조하는 context vector를 얻게됩니다. 이후 context vector와 이전단어, hidden state를 통해서 다음 단어를 확률적으로 예측하게 됩니다.

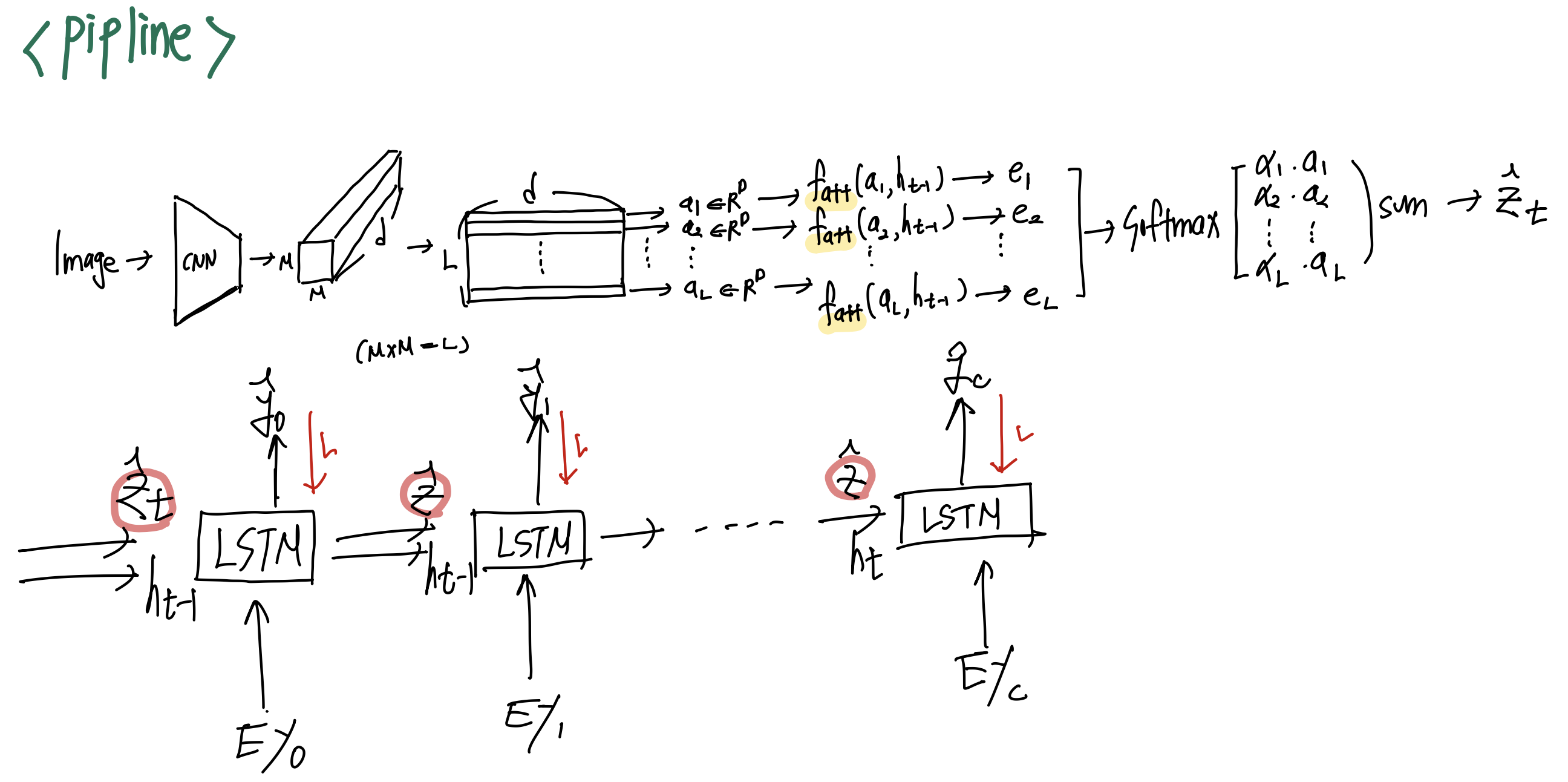
1줄 요약 : 단어 예측 마다 이미지의 특정 영역에 집중하여 단어를 확률적으로 예측하게 됩니다.

Learning Stochastic “Hard” vs Deterministic “Soft” Attention

Stochastic “Hard” Attention

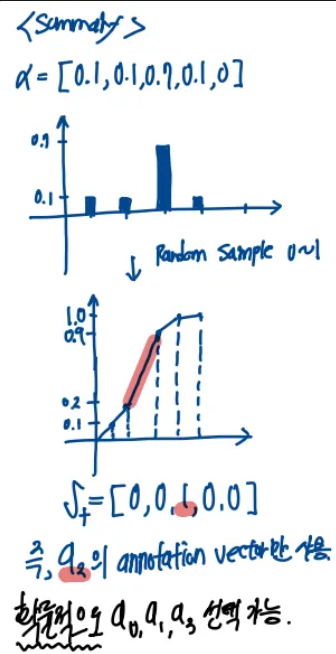
모델은 먼저 이전 단어들과 이미지의 여러 영역에서 추출된 annotation vector들을 사용하여, 각 영역이 선택될 확률 를 softmax로 계산합니다.

이 확률들은 해당 영역이 t번째 단어 생성 시 선택될 상대적 중요도를 나타내며, 모든 의 합은 1이 됩니다.

그런 다음, 하드 어텐션 방식에서는 이 확률 분포에 따라 하나의 영역을 무작위로 샘플링하여, 그 영역에 해당하는 원-핫 벡터 에서 선택된 인덱스만 1의 값을 갖게 됩니다.

이때 선택된 영역의 annotation vector만이 컨텍스트 벡터 로 사용되어, LSTM 디코더의 입력에 포함됩니다.

결과적으로, 확률적으로 높은 를 가진 영역이 선택될 가능성이 크며, 모델은 이 영역의 시각 정보를 더욱 반영하여 다음 단어를 생성하게 됩니다.

p(s_{t,i}=1 \mid s_{j<t}, a) = \alpha_{t,i}

\hat{z}_t = \sum_{i} s_{t,i}\,a_i.

다음으로는 Loss function을 정의하게 됩니다. 해당 모델의 최종 목표는 이미지를 토대로 단어를 예측하는 것이기에 $logp(y|a)$ 를 최대화 하는 것이 모델의 목표입니다. 하지만 모든 a에 대한 확률을 직접 gradient를 통해서 구하는 것은 매우 복잡합니다. 그래서 변분하한을 사용하여 이를 근사화 하는 방법을 사용하게 됩니다. 잠재변수 s를 사용하여 변분 하한을 식으로 풀면 다음과 같은 식을 얻을 수 있게 됩니다.

L_s = \sum_{s} p(s \mid a) \log p(y \mid s,a) \\ \le \log \sum_{s} p(s \mid a) p(y \mid s,a) \\ = \log p(y \mid a)

위의 식은 jensen 부등시에 의해서 다음과같이 하한을 구할 수 있게 됩니다. 즉, 해당 모델의 원래 목표였던

$\log p(y \mid a)$ 의 Lower Bound를 구하게 되었습니다. 이후 $L_s$ 를 최대화 하기 위해서 위의 식을 W에 대해서 미분하면 아래와 같은 식을 얻을 수 있게 됩니다.

\frac{\partial L_s}{\partial W} =\sum_{s} p(s \mid a) \frac{\partial \log p(y \mid s,a)}{\partial W} +\sum_{s} \log p(y \mid s,a) \frac{\partial \log p(s \mid a)}{\partial W}.

하지만 여전히 모든 S에 대해서 샘플링을 진행해야 되기때문에 complexity가 높습니다. 그래서 해당 논문에서는 Monte Carlo 방법을 사용하여 N개의 s를 샘플링하여 사용하게 됩니다. 이를 통해서 가중평균이 아닌 일반 평균으로 식을 근사할 수 있게 됩니다.

s_t \sim \text{Multinoulli}_L(\{\alpha_i\}).

\frac{\partial L_s}{\partial W} \approx \frac{1}{N} \sum_{n=1}^{N} \left[ \frac{\partial \log p(y \mid \tilde{s}^n,a)}{\partial W} + \log p(y \mid \tilde{s}^n,a) \frac{\partial \log p(\tilde{s}^n \mid a)}{\partial W} \right].

이후 추가로 Monte Carlo 방식으로 샘플링을 진행했기 떄문에 Variance가 증가할 수 있습니다. 이를 방지하기 위해서 moving average baseline 기법을 적용하였고, 추가로 분포의 일관성을 위해서 Emtropy term을 추가하여 최종 손실함수를 구현하게 됩니다. 그리고 강화학습과 같이 보상 시스템을 적용하였습니다. 최종적으로 아래와 같은 손실 함수를 얻게 됩니다.

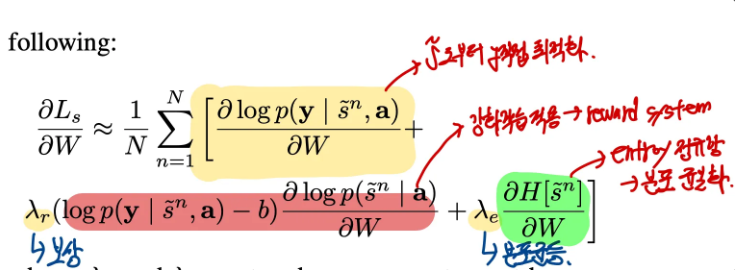
\frac{\partial L_s}{\partial W} \;\approx\; \frac{1}{N} \sum_{n=1}^{N} \Bigl[   \frac{\partial}{\partial W}\,\log p\bigl(y \mid \tilde{s}^n, a\bigr)   \;+\;   \lambda_r\,\bigl(\log p\bigl(y \mid \tilde{s}^n, a\bigr) - b\bigr)\,\frac{\partial}{\partial W}\,\log p\bigl(\tilde{s}^n \mid a\bigr)   \;+\;   \lambda_e\,\frac{\partial}{\partial W}\,\mathcal{H}\bigl[\tilde{s}^n\bigr] \Bigr].

Hard attention 과정 정리

$logP(y|a)$ 를 직접 구할 수 없기에 ELBO를 구한다.
ELBO를 최적화 할 때 Monte carlo sampling을 사용한다.
안정성을 위해 average moving baseline + entropy term을 추가한다.

Deterministic “Soft” Attention

Soft Attention(결정적 어텐션)은 이미지나 입력 시퀀스의 각 부분에 대해 소프트맥스 방식으로 연속적인 가중치 $\alpha_i$ 를 계산한 후, 이 가중치들을 사용하여 모든 부분을 부드럽게 결합해 컨텍스트 벡터 $\hat{z}_t$ 를 생성하는 방법입니다. 즉, 각 위치의 특징 $a_i$ 가 $\alpha_i$ 라는 가중치를 받아 전체 컨텍스트가 아래와 같이 계산됩니다.

\mathbb{E}_{s_t \mid a}\bigl[\hat{z}t\bigr] = \sum{i=1}^{L} \alpha_i \, a_i.

이 방식의 주요 특징은 다음과 같습니다:

연속적 가중치: $\alpha_i$ 는 확률처럼 보이나 실제로는 연속 값이기 때문에 미분이 가능하며, 모든 입력 부분을 조금씩 활용할 수 있습니다.

엔드 투 엔드 학습: 모델 전체가 미분 가능하므로, 별도의 샘플링이나 REINFORCE 같은 복잡한 확률적 기법 없이 표준 역전파(backpropagation)로 쉽게 학습할 수 있습니다.

안정적 수렴: Hard Attention(0/1 선택 방식)과 달리, Soft Attention은 각 위치에 대해 분산이 작아 보다 안정적으로 수렴하는 경향이 있습니다.

이러한 장점 덕분에 Soft Attention은 이미지 캡셔닝, 기계 번역 등 다양한 응용 분야에서 간단하면서도 효과적인 접근법으로 널리 사용됩니다. 또한, 어텐션 가중치를 시각화하면 모델이 어느 부분에 집중하는지 직관적으로 확인할 수 있어 해석 가능성이 높아집니다.

한편, Soft Attention을 사용할 때 최종 출력 확률을 계산하기 위해 Normalized Weighted Geometric Mean (NWGM)라는 수식을 사용할 수 있습니다. NWGM은 어텐션을 통해 얻은 선형 변환 값들의 기대값에 기반하여, 소프트맥스의 기댓값을 근사하는 역할을 합니다. 구체적으로, k번째 단어의 예측 확률은 다음과 같이 표현됩니다.

\text{NWGM}\bigl[p(y_t = k \mid a)\bigr] = \frac{\sum_{i} \exp\bigl(n_{t,k,i}\bigr)\,p(s_{t,i}=1 \mid a)}{\sum_{j} \exp\bigl(n_{t,j,i}\bigr)\,p(s_{t,i}=1 \mid a)} = \frac{\exp\Bigl(\mathbb{E}{s_t \mid a}\bigl[n{t,k}\bigr]\Bigr)} {\sum_{j} \exp\Bigl(\mathbb{E}{s_t \mid a}\bigl[n{t,j}\bigr]\Bigr)}.

여기서 $n_{t,k,i}$ 는 어텐션이 적용된 후의 선형 변환 결과로, $\mathbb{E}{s_t \mid a}[n{t,k}]$ 는 어텐션 위치 s_t에 대한 기댓값을 의미합니다. Baldi와 Sadowski (2014)의 연구 결과에 따르면, 소프트맥스의 NWGM은 실제 출력 확률의 기댓값과 근사적으로 동일하기 때문에, 확률적 어텐션에서의 복잡한 샘플링 과정을 단순하게 기대값 계산으로 대체할 수 있습니다.

Experiments

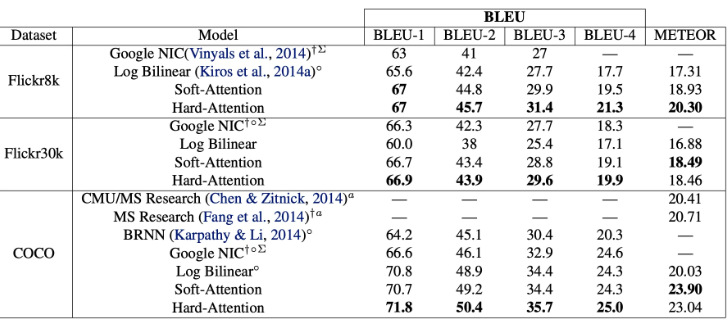
나의 생각

단어를 생성하는 경우 특정한 부분만 집중해서 모든 Hard attention의 경우 매 입력마다 서로 다은 결과가 나오기에 안정성 측면에서는 매우 불리한것 같다. 예를들어 이미지 자체에서 drop out을 사용하고, LSTM 자체에서 drop out을 사용하게 되면 확률적으로 전혀다른 결과를 만들어 낼 수 도 있다고 생각한다. 그래서 실험적으로는 Hard Attention이 주로 더 높은 성능을 보여줌을 확인하였지만, soft attention 기법이 조금더 연구가치가 있어보인다. 추가적으로 self attention이 나오기 전 논문이라서 그런지 addative attention을 사용하여 이미지와 hidden state를 결합하는 방식에서 과연 addative attention이 이미지의 전반적인 내용을 잘 담도록 결합되는지는 개인적으로 의문이 계속든다.