[ML/DL] 경사하강법(Gradient Descent)

양승웅·2024년 1월 24일

Deep Learning

목록 보기

1/1

📢 개요

인공지능의 경우 최적의 학습 패턴을 위해 자신의 Parameter를 검증해야 하며 검증 과정에서 손실함수(Loss Function)을 사용한다. 만약, 검증 단계에서 손실함수의 값이 가장 낮은 Parameter를 발견하였다면 해당 Parameter가 최적의 Parameter임이 검증 되는 것이다. 이러한 일련의 과정은 모델의 최적화(Optimization) 과정에 해당한다. 모델을 최적화하기 위한 알고리즘은 여러 종류가 있지만, 그 중에서도 가장 기본적인 최적화 알고리즘에 해당하는 경사하강법(Gradient Descent)에 대해서 포스트를 정리해보고자 한다.

✏️ 경사하강법(Gradient Descent)이란?

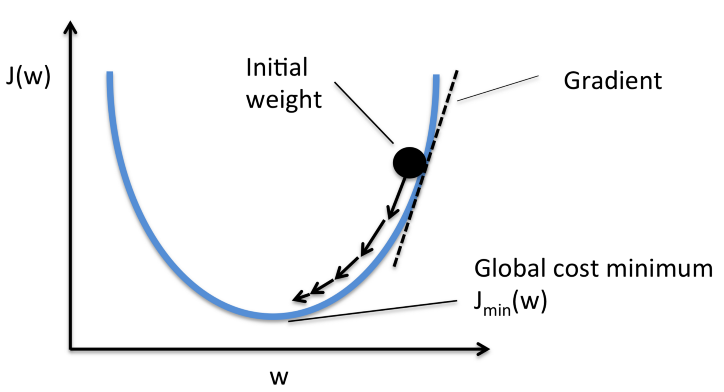
\boxed{W_{t+1} = W_t - \alpha × \frac{\partial L}{\partial W_t} \alpha : LearningRate}

👉 기울기를 이용하여 모델의 가중치를 업데이트 해가면서 예측값과 실제값 간의 차이를 줄여주기 위한, 즉 손실함수의 최솟값(최적해)를 찾아가는 기법
👉 현재 위치에서 기울기의 반대 방향으로 이동하면서 최솟값을 찾아가는 방법

📌 기울기를 직접 계산 하지 않고 경사하강법을 사용하는 목적?

일반적으로 실제 함수들은 간단하지 않고 대부분 복잡한 고차원 비선형의 형태를 갖기 때문에, 이들을 미분을 통해 계산하기는 매우 어려움
$\rightarrow$ 경사하강법을 사용하여 손실함수의 최적해를 찾는다!

🔎 작동 원리

STEP#1 기울기 $\nabla L(W)$ 계산

최적화하고자 하는 함수의 기울기를 계산하여, 절댓값과 그 부호를 확인

STEP#2 Learning Rate 설정

Learning Rate(or Step Size) $\alpha$ 를 임의로 설정하여, 이동하고자 하는 거리만큼 점을 이동

STEP#3 Weight Update

기울기와 학습률을 이용하여 가중치를 업데이트
기울기가 양수인 경우 가중치는 감소하고, 기울기가 음수인 경우 가중치는 증가함
가중치가 업데이트된 점에서 기울기를 새로 구하여 0에 수렴하는지 확인

STEP#4 반복

위 일련의 과정을 반복하여 최솟값에 도달할 때 까지 가중치를 계속해서 업데이트

📌 학습률(Learning Rate)이란?

👉 매 가중치에 대해 구해진 기울기 값을 얼마나 경사하강법에 적용할지를 결정하는 HyperParameter
👉 모델이 학습을 진행할 때 각각의 가중치를 얼마나 업데이트할지 결정

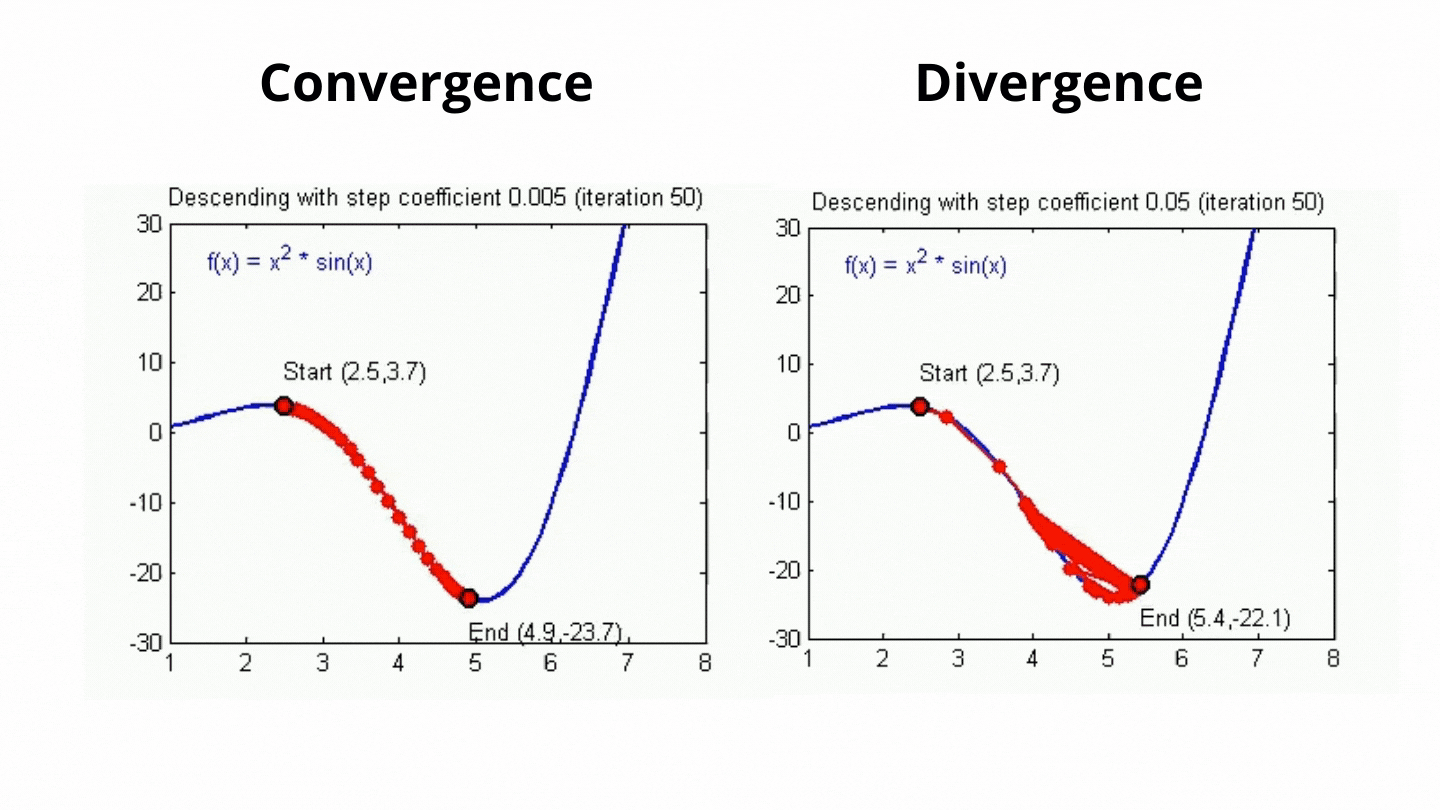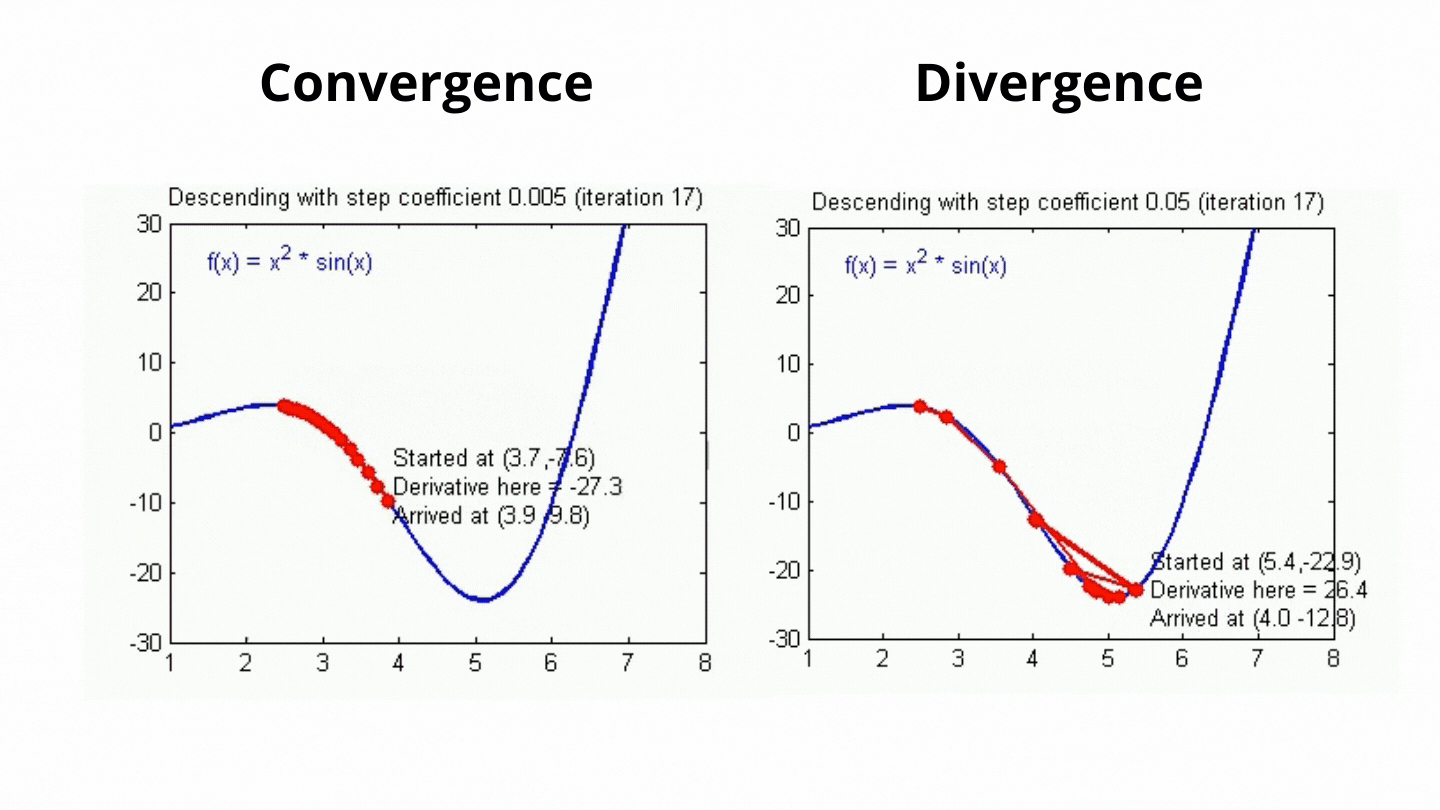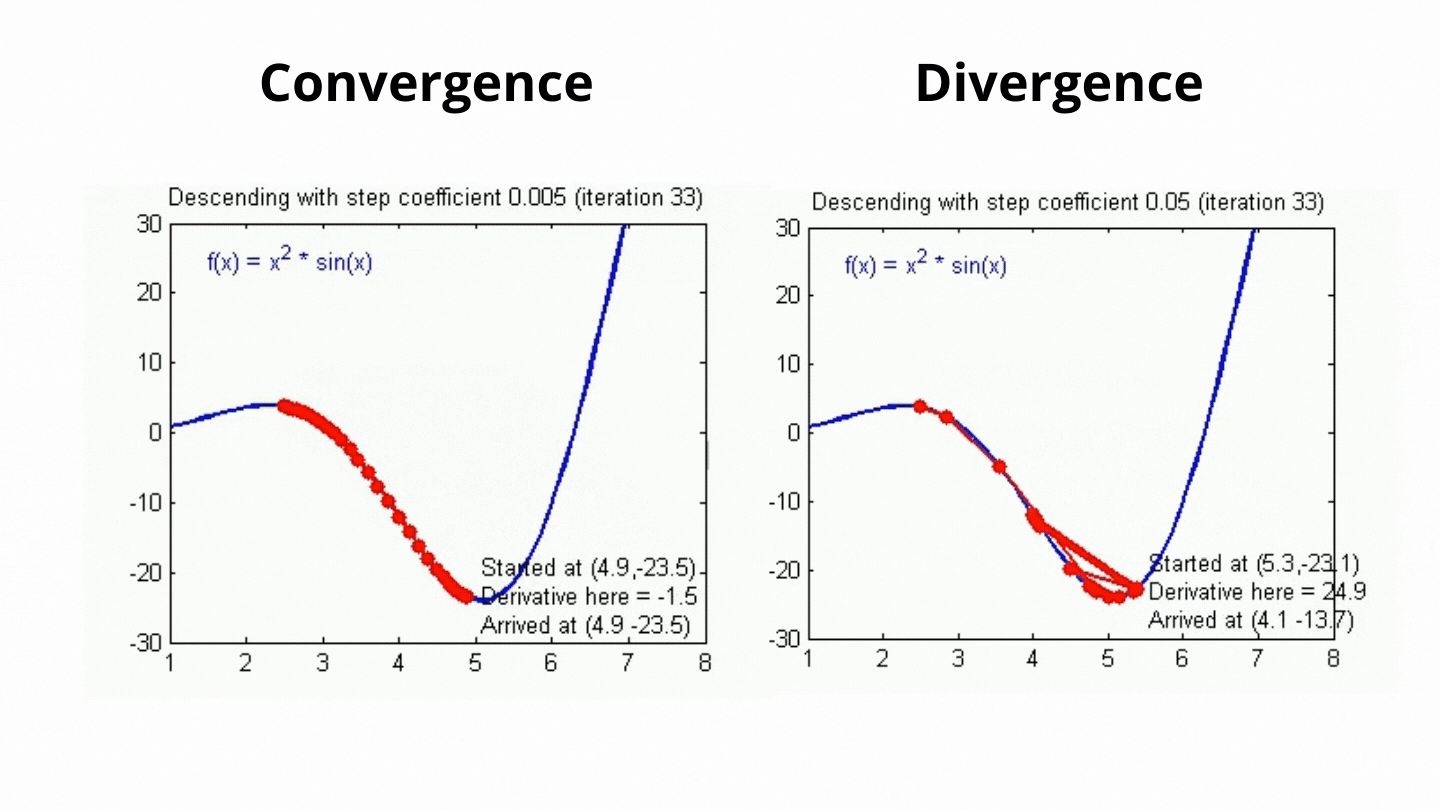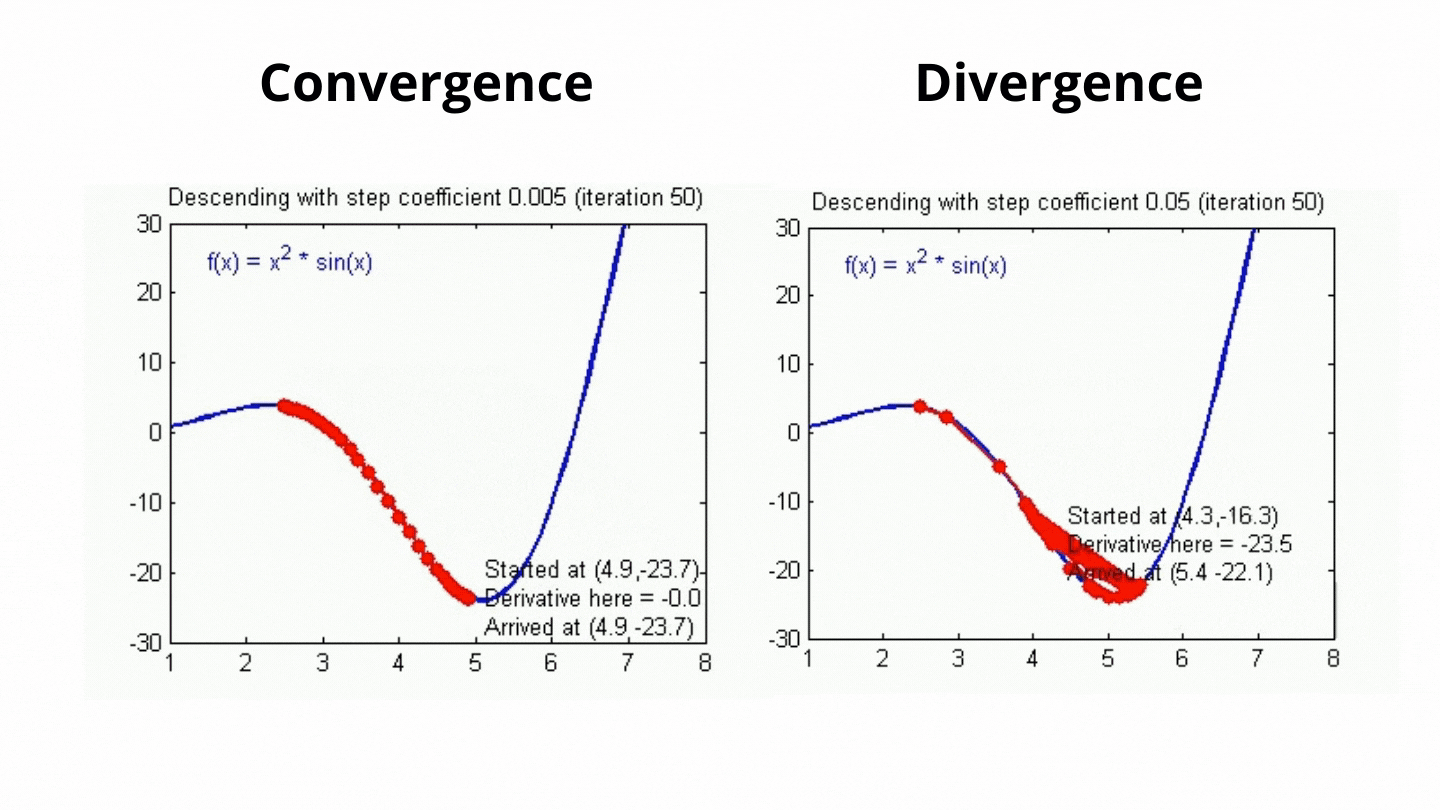
⭐ 학습률이 클 경우, 업데이트 1회에 이동하는 거리가 크기 때문에, 즉 가중치가 크게 업데이트 되므로 최솟값에 빠르게 수렴할 수 있다는 장점이 있으나, 최솟값으로 수렴하지 못하고 발산할 가능성이 존재

⭐ 학습률이 작을 경우, 모델을 안정적으로 최솟값으로 수렴시킬 수 있다는 장점이 있으나, 수렴하기까지 오랜 시간이 소요

$\therefore$ 모델의 성능을 향상시키기 위해선 적절한 학습률을 찾는 것이 중요!

🔥 한계

1. Learning Rate 설정

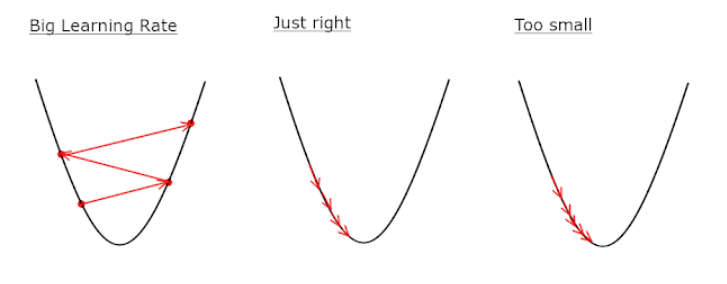
👉 학습률이 너무 높거나 너무 낮을 경우, 위 그림과 같은 문제들이 발생하므로 학습률을 적절히 조정하는 것이 매우 중요하나 이는 매우 어려움

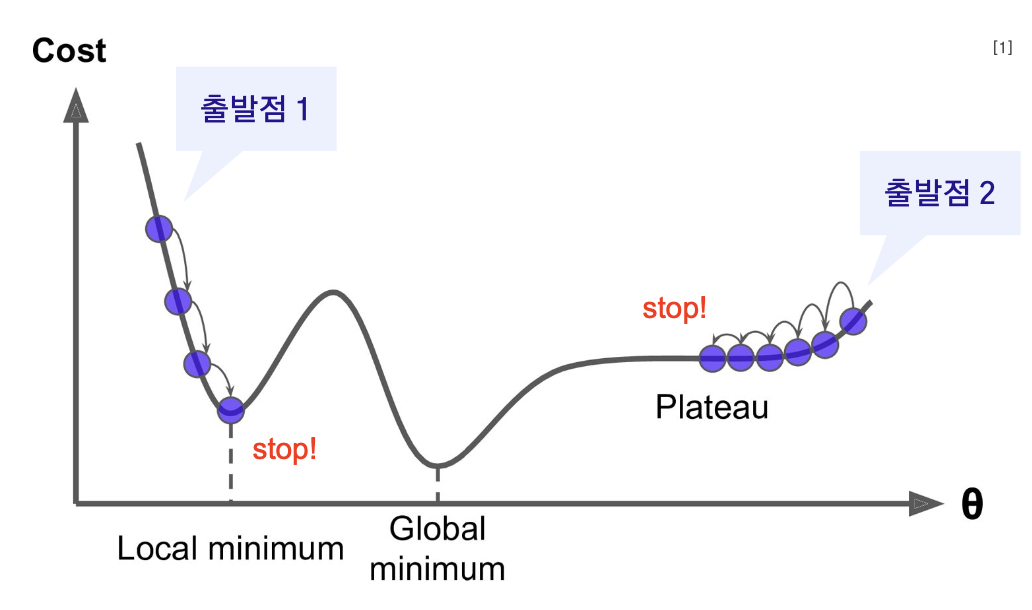
2. Local Minima 문제

👉 손실함수의 최저점(Global Minimum)이 아닌 지역최적해(Local Minimum)로 수렴하는 현상

👉 최적화의 최종 목표는 전역최적해(Global Minima)를 찾는 것이지만, 시작 위치가 랜덤하므로 Local Minima에 빠질 위험이 존재

👉 Local Minima 역시 기울기가 0이므로 가중치가 더 이상 업데이트 되지 못하는 문제 발생

3. Plateau 문제

👉 손실함수의 평탄한 영역은 기울기가 0에 가까울 정도로 매우 낮기 때문에, 학습속도가 매우 느려지게 됨

👉 이런 지점에서 경사하강법을 이용하면 더 이상 가중치가 업데이트 되지 못하고 전역 최솟값을 갖는 지점이 아닌 점에서 정지해버리는 가중치 소실(Gradient Vanishing) 문제가 발생

👉 Local Minima에 비해 상대적으로 자주 발생하는 현상

📚 알고리즘 종류

1. Batch Gradient Descent(BGD)

👉 전체 학습 데이터 세트를 사용하여 경사하강법을 수행하는 최적화 알고리즘

👉 전체 학습 데이터를 하나의 batch로 묶어 오차를 구한 뒤 기울기를 한 번만 계산하여 모델의 가중치를 업데이트

👉 1 Epoch 당 1회 Parameter 업데이트

⭐ 장점

전체 데이터에 대해 업데이트가 한 번에 이루어지기 때문에 전체 계산 횟수는 적음
전체 데이터에 대한 기울기를 계산하기 때문에 안정적으로 수렴

🔥 단점

한 번에 모든 학습 데이터 세트를 사용하므로 학습이 오래 걸림
전체 학습 데이터에 대한 오차를 모델의 가중치 업데이트가 이루어지기 전까지 축적해야 하므로 많은 메모리 용량 요구됨
Local Minima에 빠지면 빠져나오기가 어려움

❓ 용어 정리

🧩 Batch

모델의 가중치들을 한번 업데이트 시킬 때, 사용하는 데이터들의 집합

iteration 1회 당 사용되는 학습 데이터 세트의 묶음

🧩 Batch Size

Batch의 크기, 즉 모델의 가중치들을 한 번 업데이트 시킬 때 사용하는 데이터의 개수를 의미

🧩 Epoch

모델이 전체 데이터를 모두 사용하여 학습을 한 횟수

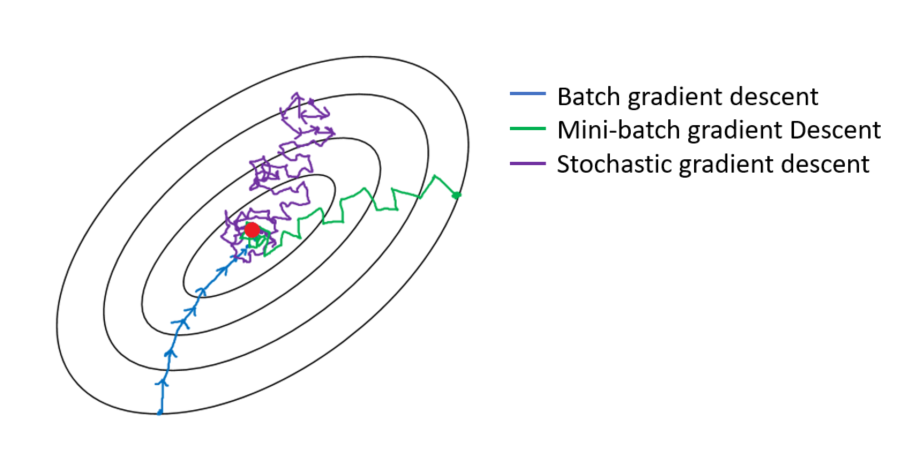
2. Stochastic Gradient Descent(SGD)

👉 전체 학습 데이터 세트에서 무작위로 추출한 데이터 한 개에 대해서만 경사하강법을 수행하는 최적화 알고리즘

👉 무작위로 추출된 개별 데이터에 대한 손실값의 기울기는 약간씩 다르기 때문에 기울기의 방향이 매번 크게 바뀜
$\rightarrow$ 수렴 과정에서 Shooting이 발생

⭐ 장점

BGD에 비해 학습 데이터가 적으므로 학습 속도가 빠름
수렴 과정에서 발생하는 Shooting이 Local Minima에 빠질 확률을 줄여줌

🔥 단점

한 번의 반복에 한 번의 데이터만 사용하기 때문에 전역최적해를 찾지 못할 가능성 존재
데이터를 한 개씩 처리하기에 GPU의 성능을 최대로 활용할 수 없음

3. Mini-Batch Gradient Descent(MSGD)

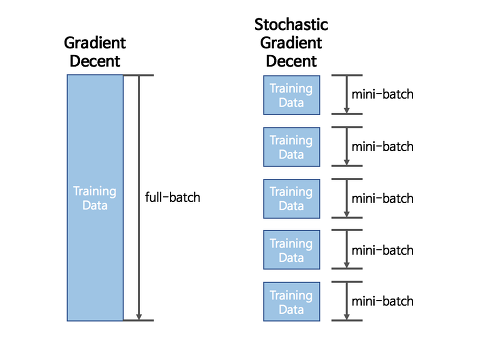
👉 전체 데이터 세트를 여러 개의 mini-batch로 나누어 한 개의 mini-batch 마다 경사하강법을 수행하는 최적화 알고리즘

❓ 만약, 전체 데이터가 1000개인 데이터를 학습시킬 때, batch_size가 100일 경우?
$\rightarrow$ 전체 데이터를 100개씩 총 10묶음의 배치로 나누어 1 Epoch 당 10번 경사하강법을 수행하는 것!

👉 수렴 과정에서 Shooting이 발생하기는 하지만, 한 batch의 손실값의 평균으로 경사하강법을 실시하기 때문에 SGD만큼 심하진 않음

⭐ 장점

한 번 학습시, 전체 학습 데이터가 아닌 일부 학습 데이터만 사용하기 때문에 BGD보다 계산량이 적음
Shooting이 적당히 발생하므로 Local Minima를 어느정도 피할 수 있음

🙏 Reference

https://seamless.tistory.com/38
https://light-tree.tistory.com/133
https://heung-bae-lee.github.io/2019/12/08/deep_learning_02/

양승웅

[ML/DL] 경사하강법(Gradient Descent)

Deep Learning

📢 개요

✏️ 경사하강법(Gradient Descent)이란?