📢 개요
✏️ K-Means Clustering이란?
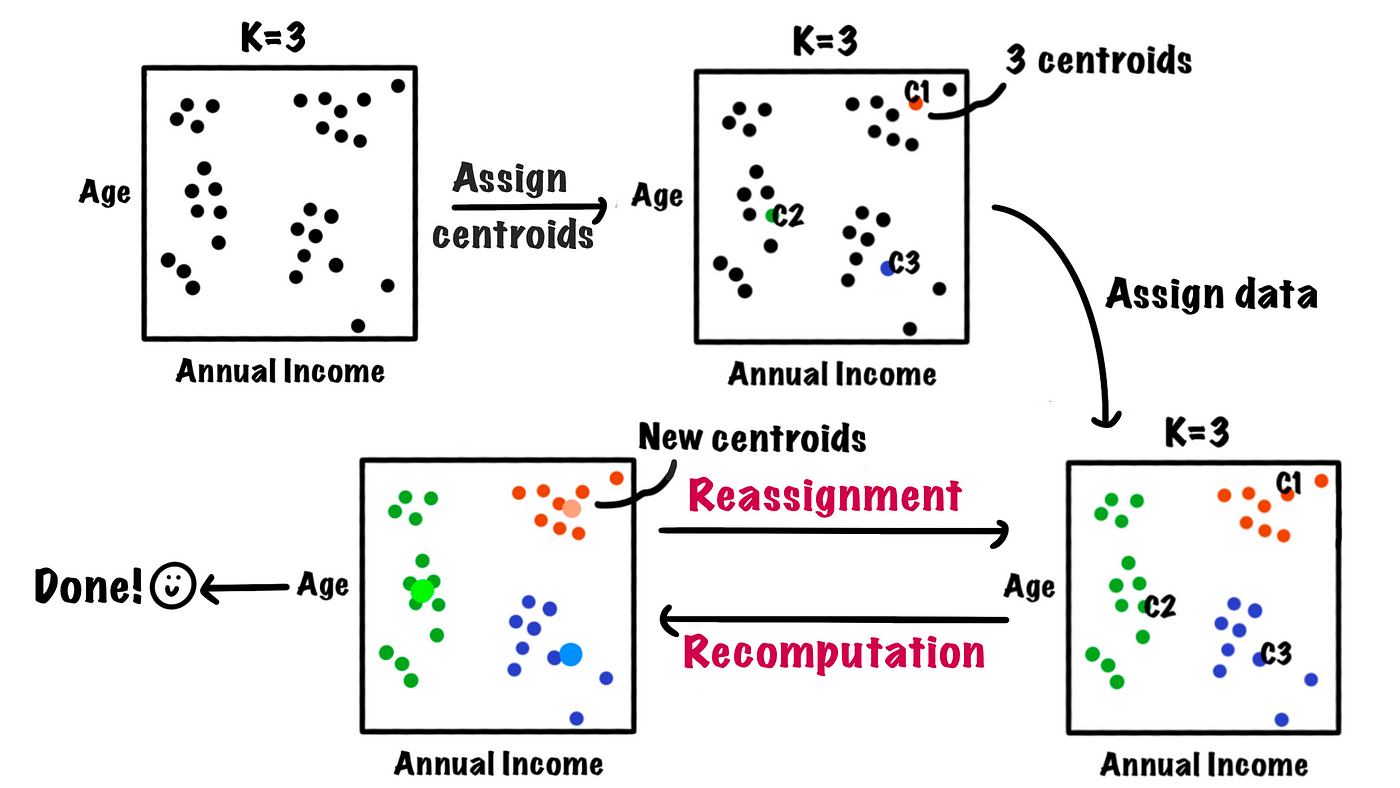
👉 임의의 지점을 선택하여 군집 중심점(Centroid)으로 설정하고, 해당 중심점에서 가장 가까운 개별 데이터들을 선택하는 군집화 알고리즘
👉 레이블이 없이, 데이터들 간의 유사성을 기반으로 각 데이터의 그룹을 할당해 나가는 비지도학습 알고리즘
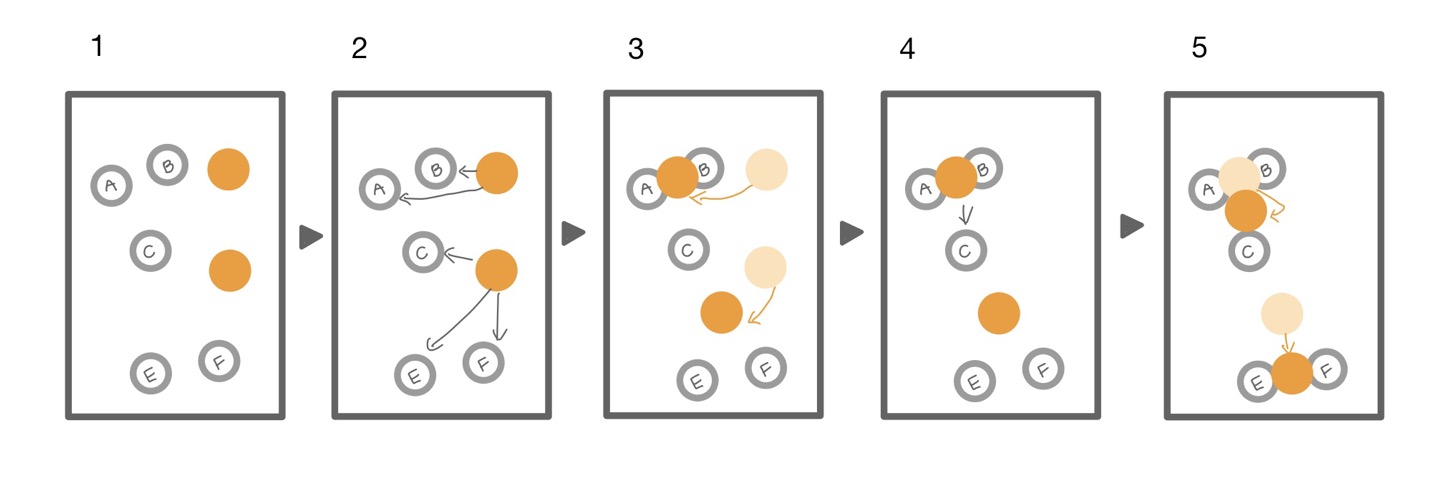
🔎 작동 원리
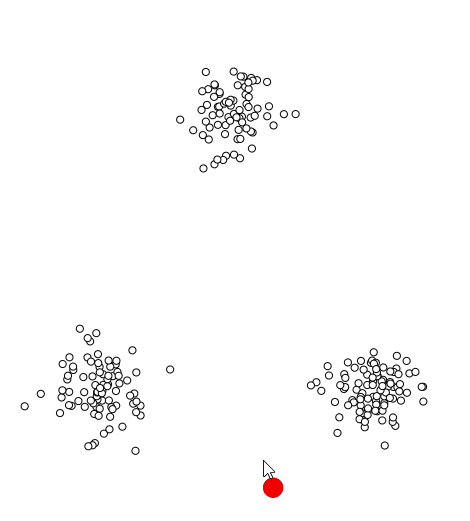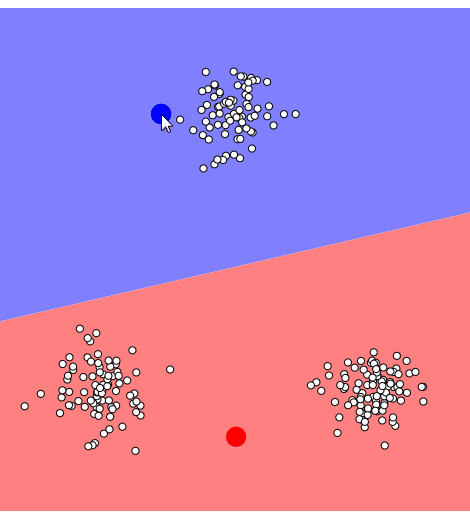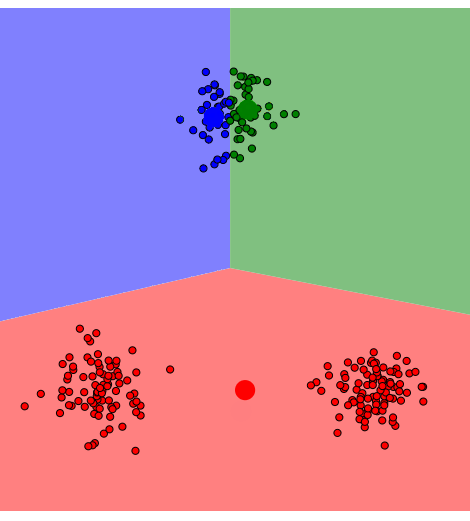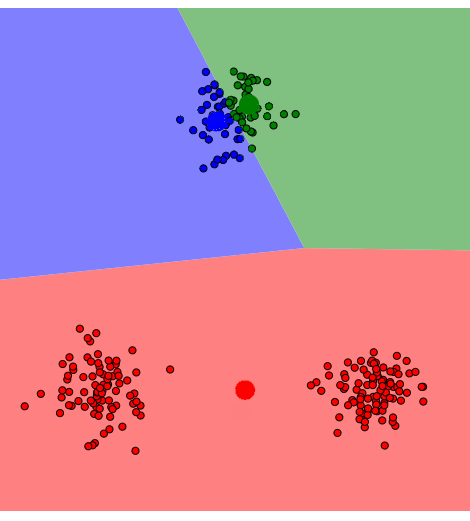
STEP#1. 군집 개수 k값 결정
STEP#2. 임의의 초기 군집 중심점(Centroid) 설정
STEP#3. 모든 샘플을 순회하여, 개별 샘플을 가장 가까운 중심점이 있는 군집으로 할당
STEP#4. 초기 중심점을, 할당된 샘플들의 평균 중심으로 이동
STEP#5. 군집의 중심점에 변화가 없을 때 까지, 혹은 사용자가 임의로 지정한 최대 반복횟수에 도달할 때까지 3-4번 과정 반복 수행
📚 성능 평가 지표
👉 비지도학습의 경우 데이터 세트에 레이블이 없기 때문에, 지도학습에서 사용되던 성능 평가 기법들을 적용할 수 없는 문제
👉 군집의 성능을 평가하기 위해서는 알고리즘 자체의 지표를 사용해야 함
📗 최적의 K(군집 개수) 찾기
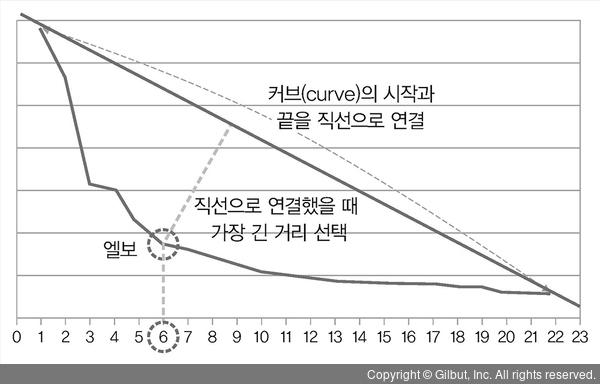
1. 엘보우 기법(Elbow Method)
👉 군집의 개수를 증가시켰을 때 나타나는 inertia(관성) 변화 그래프를 관찰하여 최적의 군집 개수 K를 찾는 기법
👉 군집의 수를 계속해서 증가시켰을 때, 더 이상 정확도가 향상되지 않는 지점이 최적의 k값을 갖는 지점
❓ inertia(관성) = distortion(왜곡)
- 군집의 중심점과 샘플 간의 거리제곱합(SSE)을 의미 = WCSS(Within Cluster Sum of Squared)
- 군집에 속한 샘플들이 얼마나 가깝게 모여있는지를 나타내는 지표
군집의 수가 많아질 수록, 샘플과 중심점 간의 거리가 더 가까워지므로 inertia 역시 감소할 것.
💻 코드 예제
distortions = []
for i in range(1, 11) :
km = KMeans(n_clusters=i,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
km.fit(X)
distortions.append(km.inertia_)
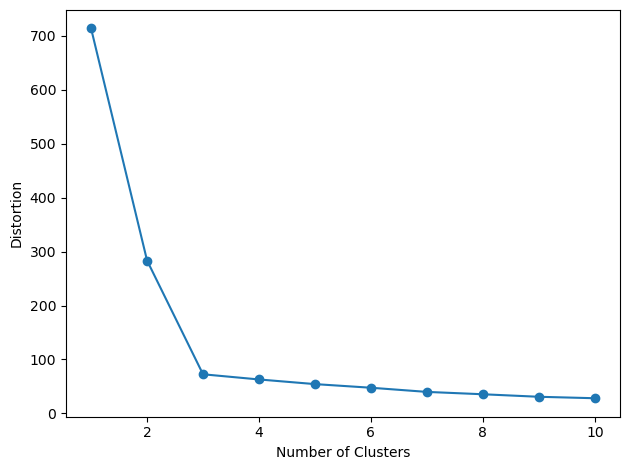
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of Clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()# result2. 실루엣 기법(Silhouette Method)
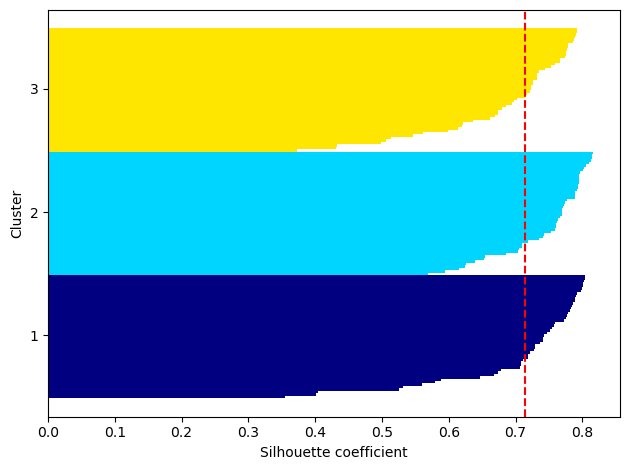
👉 샘플들이 할당된 군집의 일관성을 측정하여 최적의 군집 개수 K를 찾는 기법
실루엣 계수(Silhouette coefficient)
: 해당 샘플과 같은 군집에 속해있는 다른 샘플들과의 거리 평균
: 해당 샘플이 속하지 않는 군집 중 가장 가까운 군집과의 평균 거리
👉 실루엣 계수 값이 크면, 해당 샘플이 속해있는 군집과 잘 일치하고 인접한 군집과 잘 일치하지 않음을 나타냄
군집 결과가 우수함을 의미 !
👉 일반적으로 각 군집 내 샘플들의 실루엣 계수(Silhouette Coefficient) 평균값이 0.7보다 크면 군집 성능이 좋다고 판단
💻 코드 예제
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=['sepal_length', 'sepal_width', 'petal_length', 'petal_width'])
km = KMeans(n_clusters=3,
init='k-means++',
max_iter=300,
random_state=0)
km.fit(df)
df['cluster'] = km.labels_
# 각 샘플의 Silhouette Coefficient 계산
score_samples = silhouette_samples(iris.data, labels=df.cluster)
df['silhouette_coeff'] = score_samples
# 모든 샘플들의 Silhouette Coefficient의 평균을 계산
average_score = silhouette_score(iris.data, labels=df.cluster)
print(f'Iris data Silhouette Analysis Score : {average_score : .3f}')
print(df.groupby('cluster')['silhouette_coeff'].mean())# result
Iris data Silhouette Analysis Score : 0.553
cluster
0 0.417320
1 0.798140
2 0.451105
Name: silhouette_coeff, dtype: float641번 군집은 실루엣 계수의 평균값이
km = KMeans(n_clusters=3,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X,
y_km,
metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels) :
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper),
c_silhouette_vals,
height=1.0,
edgecolor='none',
color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg,
color='red',
linestyle='--')
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()# result🔥 문제점
1. 초기 군집 중심점 설정에 따라 최종 군집 성능이 다르게 나타날 수 있다
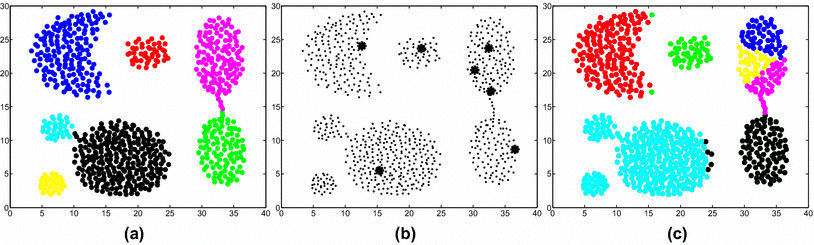
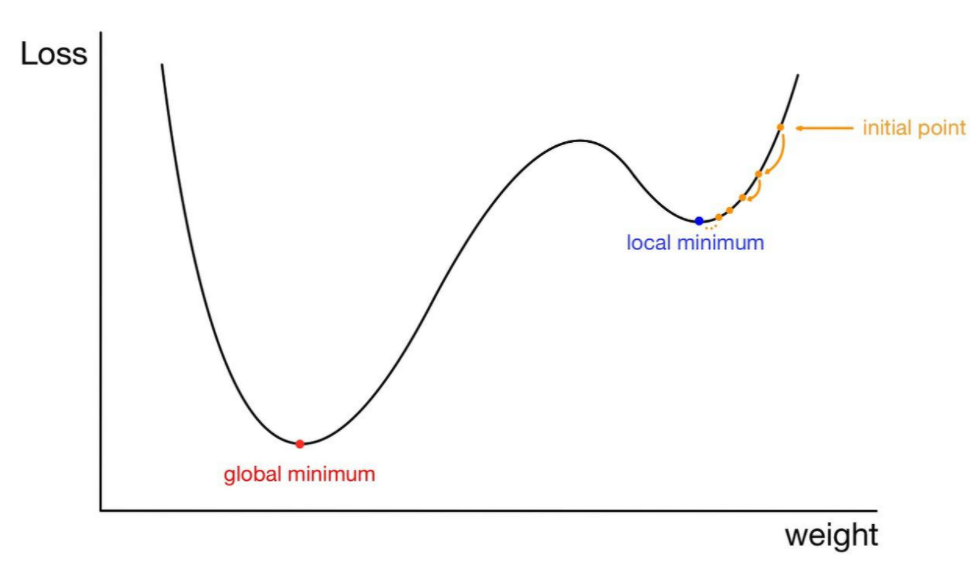
👉 초기 중심점 선정 시 무작위로 중심점을 선정하기 때문에, 중심점과 샘플 간의 거리가 local minima로 수렴하여 잘못된 군집화가 이루어질 수 있음
👉 초기 중심점을 여러 번 바꿔가면서 학습을 반복하여, global minima로 수렴하는 최적의 군집을 찾아내야 함
📌 Local Minima로 수렴하는 예시
2. 샘플들의 분산 구조를 반영하지 못한다
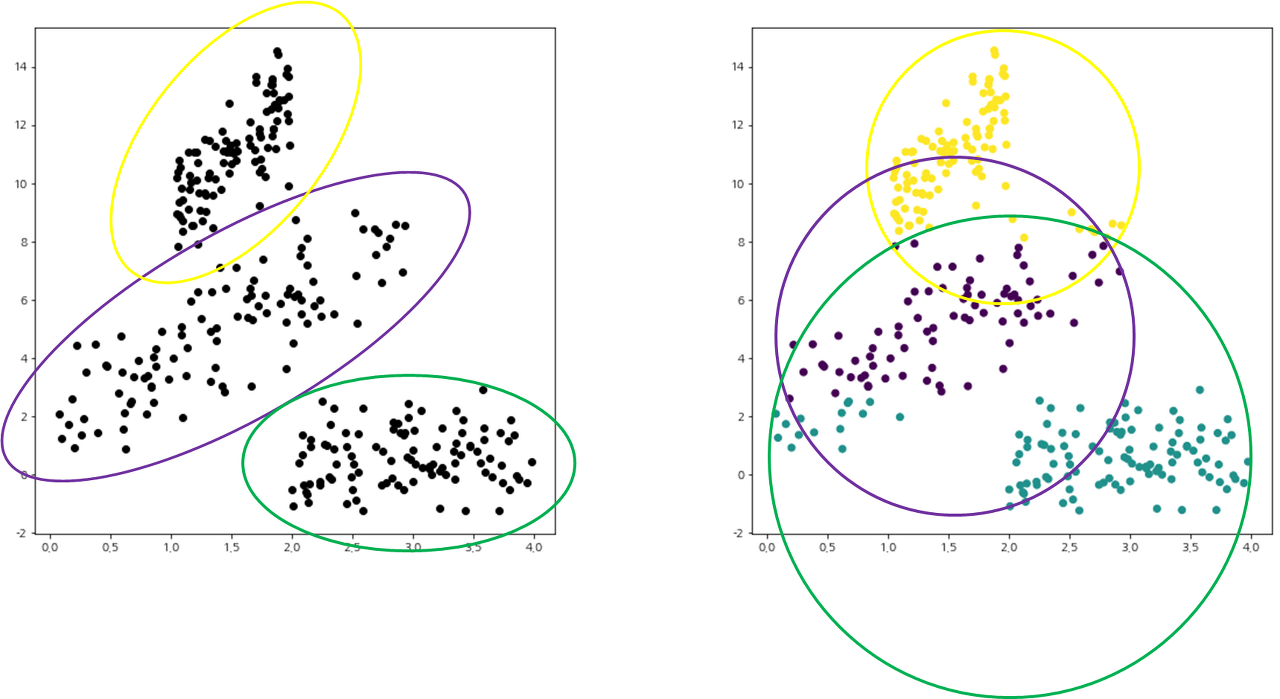
👉 Euclidean distance를 기반으로 중심점과 샘플 간의 유사도를 측정하기 때문에 분산 구조를 제대로 반영하지 못함
👉 왼쪽과 같이 3개의 타원형 구조의 군집이 형성되지 못하고, 오른쪽과 같이 원형 구조의 군집을 얻게 되는데 이는 Euclidean distance로부터 초래된 결과
3. 노이즈, 이상치에 매우 민감하게 반응한다
👉 샘플들 간의 유사도 측정을 Euclidean Distance를 기반으로 하는 알고리즘이기에 중심점을 업데이트하는 과정에서 이상치의 영향을 받을 수 있음
4. 범주형 변수를 갖는 데이터 세트에는 사용하지 못한다
👉 K-Means는 거리 기반 알고리즘이기에 범주형 변수가 있는 데이터 세트에는 적용 불가
✏️ K-Medoids Clustering = PAM(Partitioning Around Medoids)이란?
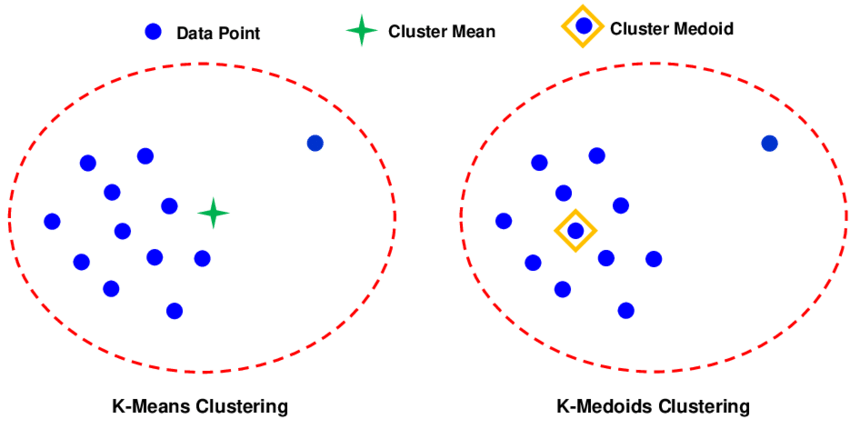
👉 초기 중심점, 잡음(Noise), 이상치(Outlier)에 매우 민감하게 반응하는 K-Means의 단점을 보완한 알고리즘
👉 실제 샘플 데이터들 중 하나를 택하여 대표 객체로 선정하고 이를 중심으로 나머지 샘플들을 군집에 할당시키는 원리
즉, 중심점을 평균 대신 중갼점을 사용
🔥 K-Medoids 알고리즘 역시 K-Means와 동일하게 Euclidean distance를 기반으로 하는 알고리즘이므로, 원형의 군집이 아닌 경우엔 군집 성능이 떨어지는 단점 존재
🔥 K-Means와 동일하게, 하이퍼파라미터 k(군집 개수)에 따라 군집 성능이 달라지므로 최적화 과정 필요
🔥 데이터 간 모든 거리 비용을 반복하여 계산하므로 K-Means에 비해 상대적으로 많은 시간이 소요
🔎 작동 원리
STEP#1. Build
- 군집의 개수 k를 결정
- 실제 존재하는 샘플들 중에서 k개를 무작위로 선택하여 medoids로 선정
- 모든 샘플들을 가장 가까운 medoids를 중심으로 하는 군집에 할당
STEP#2. SWAP
- 하나의 medoid를 방문
- 현재 방문한 medoid에서 medoid를 제외한 모든 샘플들을 순회하면서 medoid를 넘겨줄 때 발생하는 목적함수의 개선 정도를 계산
- 목적함수가 가장 크게 개선되는 샘플로 medoid를 넘겨줌
- 다음 medoid로 이동
- medoid 이동 시 더 이상 목적함수의 개선이 발생하지 않을 경우 SWAP 종료
STEP#3. 모든 샘플들을, 가장 가까운 Medoid를 중심으로 하는 군집에 할당시키고 알고리즘 종료
🙏 Reference
https://movefast.tistory.com/307
https://itstory1592.tistory.com/19
https://gsbang.tistory.com/entry/%EA%B8%B0%EA%B3%84%ED%95%99%EC%8A%B5-k-means-%ED%81%B4%EB%9F%AC%EC%8A%A4%ED%84%B0%EB%A7%81-%EC%B5%9C%EC%A0%81%EC%9D%98-k%EA%B0%92-%ED%83%90%EC%83%89
https://wkddmswh99.tistory.com/6
https://medium.com/h-document/%ED%81%B4%EB%9F%AC%EC%8A%A4%ED%84%B0%EB%A7%81-%EA%B5%B0%EC%A7%91-%EB%B6%84%EC%84%9D-%EB%B9%84-%EA%B3%84%EC%B8%B5%EC%A0%81-%EA%B5%B0%EC%A7%91-%EB%B6%84%EC%84%9D-ef1a96948d7d
http://blog.johannesmp.com/2017/12/03/an-overview-of-k-means-clustering/