📢 개요
데이터 전처리에서 결측치 처리는 데이터의 완전성과 정확성을 유지하기 위해 필수적으로 거쳐야 하는 작업이다. 결측치를 처리하지 않고 Machine Learning, Deep Learning 학습 데이터로 사용할 경우 분석 결과의 왜곡이 발생하고 모델의 성능이 저하될 수 있으므로 적절한 대응이 필요하다. 이번 포스트에서는 데이터에서 발생할 수 있는 결측치의 유형들에는 무엇이 있는지 알아보고 이를 어떻게 처리할 수 있는지에 대해 생각해보고자 한다.
✏️ 결측치(Missing Value)란?
👉 데이터에 값이 누락된 것을 의미
👉 줄여서 NA라고 표현하기도 하며, N/A, NaN, Null로 표현되기도 함
👉 데이터를 분석하는데에 있어서 매우 방해가 되는 존재
📌 결측치 발생 원인
- 설문조사에서 참가자 중 일부가 답변하기 어렵거나 곤란한 질문에 응답하지 않았을 때
- 특정 대상을 장기간에 걸쳐서 조사하는 종단연구에서 사망, 연락두절 등의 상태가 발생했을 때
- 데이터를 입력하는 도중 실수로 값을 입력하지 못하였을 때
- 해당 항목에 적절한 값이 없어서 입력되지 못하였을 때
- 전산 상의 오류가 발생하여 입력되지 못하였을 때 등
📂 유형
- 결측치는 결측치의 발생에 어떠한 인과관계가 있는지에 따라 MCAR, MAR, MNAR로 구분

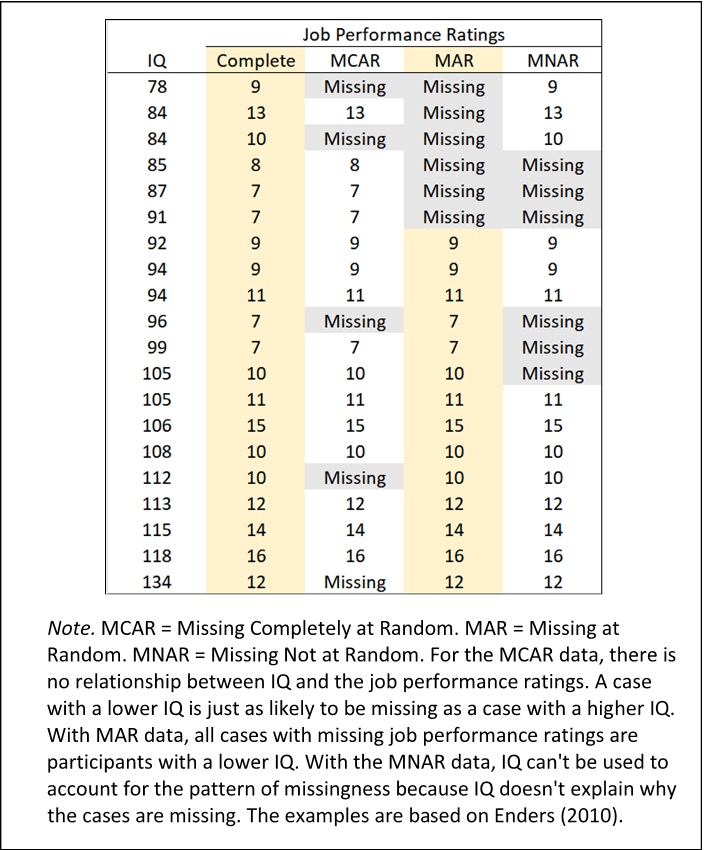
1. MCAR (Missing Completely At Random / 완전 무작위 결측)
👉 데이터의 누락이 전 범위에 걸쳐 완전히 무작위로 발생
👉 특정 변수 상에서 발생한 결측치가 다른 변수 상의 값들과 아무런 상관관계가 없음
👉 통계적으로 결측치의 영향이 다소 존재하나 편향은 없으므로 대체 가능
🧩 ex) 실수로 데이터를 입력하지 않음, 전산상의 오류 등
2. MAR (Missing At Random / 무작위 결측)
👉 데이터의 결측치가 무작위로 발생
👉 결측치가 발생한 변수의 값이 관측된 데이터의 일부 다른 변수와 상관관계가 있음
👉 다양한 결측치 대체 기법을 통해 추정이 가능
👉 통계적으로 결측치의 영향이 다소 있으나 편향은 없으므로 대체 가능
🧩 ex) 여성이 남성보다 체중을 기입하지 않는다 --> 체중 변수에 결측치가 발생하나 이는 체중 변수와 관련이 있는 것이 아닌 성별 변수와 관련이 있는 것
3. MNAR (Missing Not At Random / 비무작위 결측)
👉 결측치가 임의로 발생하지 않으며, 발생한 변수의 값과 관계가 있고 결측 사유가 분명한 경우
👉 그러나 결측치의 원인을 추정하기 어렵고 단순 결측치 대체 기법만으로는 해결하기 어려움
👉 통계적으로 결측치의 영향이 크므로 결측치의 원인에 대한 조사 후 대응 필요
🧩 ex) 우울증에 대한 설문조사에서, 실제로 우울증이 심한 경우 우울한 기분에 대해 자세히 묻는 항목에 답하는 것이 괴로워 고의로 회피
- MCAR은 결측치가 아무런 관계없이 완전히 무작위로 발생하는 이상적인 상태
- 이와 달리 MAR과 MNAR은 분명한 인과관계에 의해 결측치가 발생하는데 MAR은 그 이유가 명확하여 추정이 가능한 상태이고 MNAR은 이유를 알 수 없어 추정하기 어려운 차이점 존재
📍 예시
🔎 탐색
1. pandas를 이용한 탐색
df.info()👉 Non-Null Count를 통해 각 Column 별 결측치 개수 파악 가능
df.isnull().sum(axis=0)👉 각 Column 별 결측치 개수만을 요약하여 출력
🔥 결측치의 개수만을 파악 가능하며 결측치가 어떠한 유형인지는 파악하기 어려움
2. klib을 이용한 탐색
import klib
klib.missingval_plot(df, sort=True)
# 결측치가 있는 변수의 분포 확인
klib.dist_plot(df.weight)
klib.dist_plot(df.IQ)
klib.dist_plot(df.mid_score)
💡 처리 방법
📌 결측치 비율에 따른 처리 방법
| 결측치 비율 | 처리 방법 |
|---|---|
| 10% 미만 | Deletion or Imputation |
| 10% 이상 20% 미만 | Model-based method |
| 20% 이상 | Model-based method |
1. 제거 (Deletion)
👉 MCAR일 때만 사용 가능
👉 데이터의 손실 즉 표본의 수 감소로 통계적 검정력 저하
👉 표본의 수가 충분하고 결측값이 10-15% 이내일 때에는 결측값을 제거한 후 분석하여도 결과에 크게 영향을 주지 않음
1.1 Listwise Deletion
👉 결측치가 존재하는 행(instance) 전체를 삭제하는 방식
👉 데이터 표본의 숫자가 적은 경우 표본의 축소로 인한 검정력 감소
1.2 Pairwise Deletion
👉 분석에 사용하는 속성(attribute)에 결측치가 포함된 행만을 제거하는 방식
👉 Listwise 방법에 비해 더 많은 instance를 가지고 분석 가능
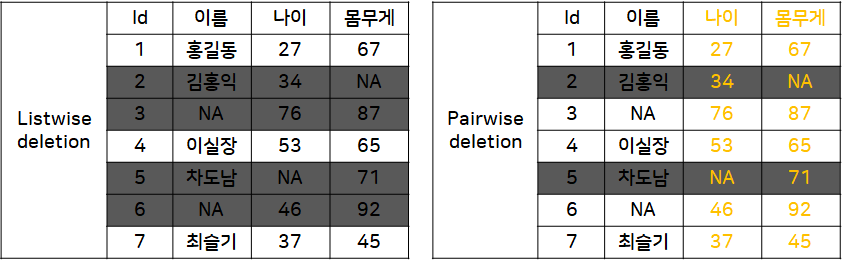
❗ Likewise의 경우 결측치(NA)가 존재하는 행 전체를 삭제하지만 Pairwise는 분석에 사용되는 '나이', '몸무게' 변수에 결측치가 존재하는 행만을 제거하는 것이 차이점
💻 코드 예시
import pandas as pd
df = pd.DataFrame({'id' : [1, 2, 3, 4, 5, 6, 7],
'이름' : ['홍길동', '김홍익', None, '이실장', '차도남', None, '최슬기'],
'나이' : [27, 34, 76, 53, None, 46, 37],
'몸무게' : [67, None, 87, 65, 71, 92, 45]})
# Listwise Deletion
df_listwise = df.dropna()
# Pairwise Deletion
df_pairwise = df.dropna(subset=['나이', '몸무게'])2. 대치 (Imputation)
2.1 단순대치법 (Single Imputation)
👉 결측치의 대체값으로 하나의 값을 선정하는 방식
👉 결측치가 무작위로 발생한 것이 아닐 경우 Mean, Correlation, Regression Coefficient와 같은 Parameter 추정치의 편향(bias) 발생
👉 이러한 추정 편향으로 인해 아예 결측값을 제거하는 것보다 통계적 특성이 더 나빠질 수 있음
2.1.1 평균값 대치 (Mean Imputation)
👉 결측치가 포함된 feature 내에서 결측치를 제외한 나머지 관측값들의 대표값(Mean, Median, Mode)으로 결측치를 대체
👉 데이터가 연속형 실수값이면서 대칭분포일 경우 평균이 좋고, 연속형 실수값이면서 왜도가 큰 분포일 경우 중앙값을 이용하는 것이 좋음
👉 데이터가 범주형이거나 정수값인 경우 최빈값을 이용
🔥 한계
- 다른 feature와의 상관관계를 고려하지 않고 결측치가 존재하는 feature만을 고려
- 데이터의 손실을 줄일 수 있어 Listwise Deletion에 비해 향상된 방법이라고 할 수 있으나 결측치의 불확실성을 고려하지 못함
- 편향된 추정치가 발생할 수 있으며 이로 인한 변수의 분산 왜곡 우려
💻 코드 예시
- scikit-learn의 SimpleImputer Class
- strategy : 대체를 어떻게 할 것인지 결정, default='mean'
- 'mean'(평균) / 'median'(중앙값) / 'most_frequent'(최빈값) / 'constant'(fill_value에서 정해진 값)
- fill_value : str or numerical value, default=None
- strategy : 대체를 어떻게 할 것인지 결정, default='mean'
from sklearn.impute import SimpleImputer
# 평균으로 대체
imputer_mean = SimpleImputer(strategy="mean")
imputer_mean_data = imputer_mean.fit_transform(data[['column_name']])
# 중앙값으로 대체
imputer_mean = SimpleImputer(strategy="median")
numeric_data = imputer_mean.fit_transform(data[['column_name']])
# 최빈값으로 대체
imputer_mean = SimpleImputer(strategy="most_frequent")
numeric_data = imputer_mean.fit_transform(data[['column_name']])
# 임의로 정해준 값으로 대체
imputer_mean = SimpleImputer(strategy="constant", fill_value=1) # 결측치를 1로 대체
numeric_data = imputer_mean.fit_transform(data[['column_name']])2.1.2 회귀 대치 (Regression Imputation)
👉 관측값과 결측치 간에 강한 상관관계가 존재한다는 가정 하에 관측치 간의 회귀식을 통해 결측치를 예측
👉 결측치가 포함되지 않은 변수를 feature(독립변수)로, 결측치가 포함된 변수를 target(종속변수)로 하여 회귀식을 구성하고, 추정 결과 얻은 회귀식의 예측값으로 결측치 대체
🔥 한계
- 결측치를 실제로 관측된 값으로 가정하고 다른 변수들을 기반으로 결측치를 예측하는 것이므로 결측치 대체의 불확실성을 고려하지 않음
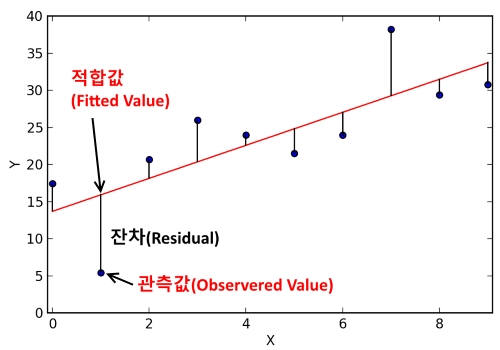
- 결측치가 fitted value(추정된 회귀선 상의 값)로 대체되기 때문에 오히려 실제 관측값보다 계수 추정 신뢰도가 과대평가되는 경향 존재
2.1.3 확률적 회귀 대치 (Stochastic regression Imputation)
👉 Regression Imputation 방법에 Random Residual Value를 추가하해주어 결측치를 예측
👉 Single Imputation 방법들 중 편향이 제일 적은 결과 보여주는 방법
🔥 한계
- 결측치가 [회귀 추정된 값(fitted value) + 잔차(residual)] 대체되어 관측값만큼 계수 추정 신뢰도를 평가
📌 잔차(Residual) : 표본으로 추정한 회귀식과 실제 관측값의 차이를 의미. 데이터 분석 시 모집단의 데이터 일부만으로 회귀식을 얻어내기 때문에 잔차를 기준으로 회귀식의 최적의 회귀계수를 결정.
💻 코드 예시
🌱 Raw data
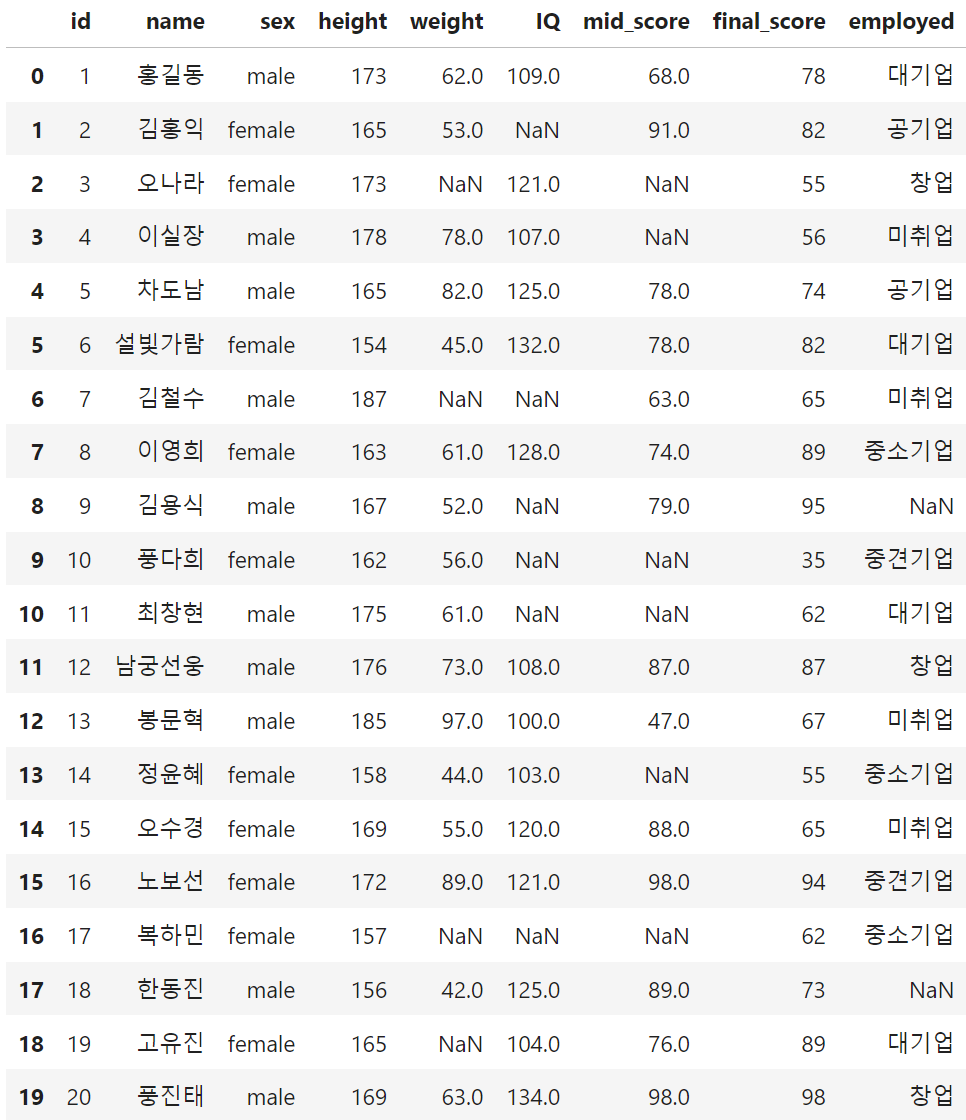
from sklearn.linear_model import LinearRegression
idx = df.weight.isnull() == True
# 훈련 세트와 테스트 세트로 분리
x_train, x_test = df[['height']][~idx], df[['height']][idx]
y_train = df[['weight']][~idx]
# 선형회귀모델 인스턴스 생성 및 학습
lm = LinearRegression().fit(x_train, y_train)
# 회귀 추정치 + Random Residual Value로 결측치 대체
df.loc[idx, 'weight'] = lm.predict(x_test) + 5*np.random.rand(4,1)🎁 Result
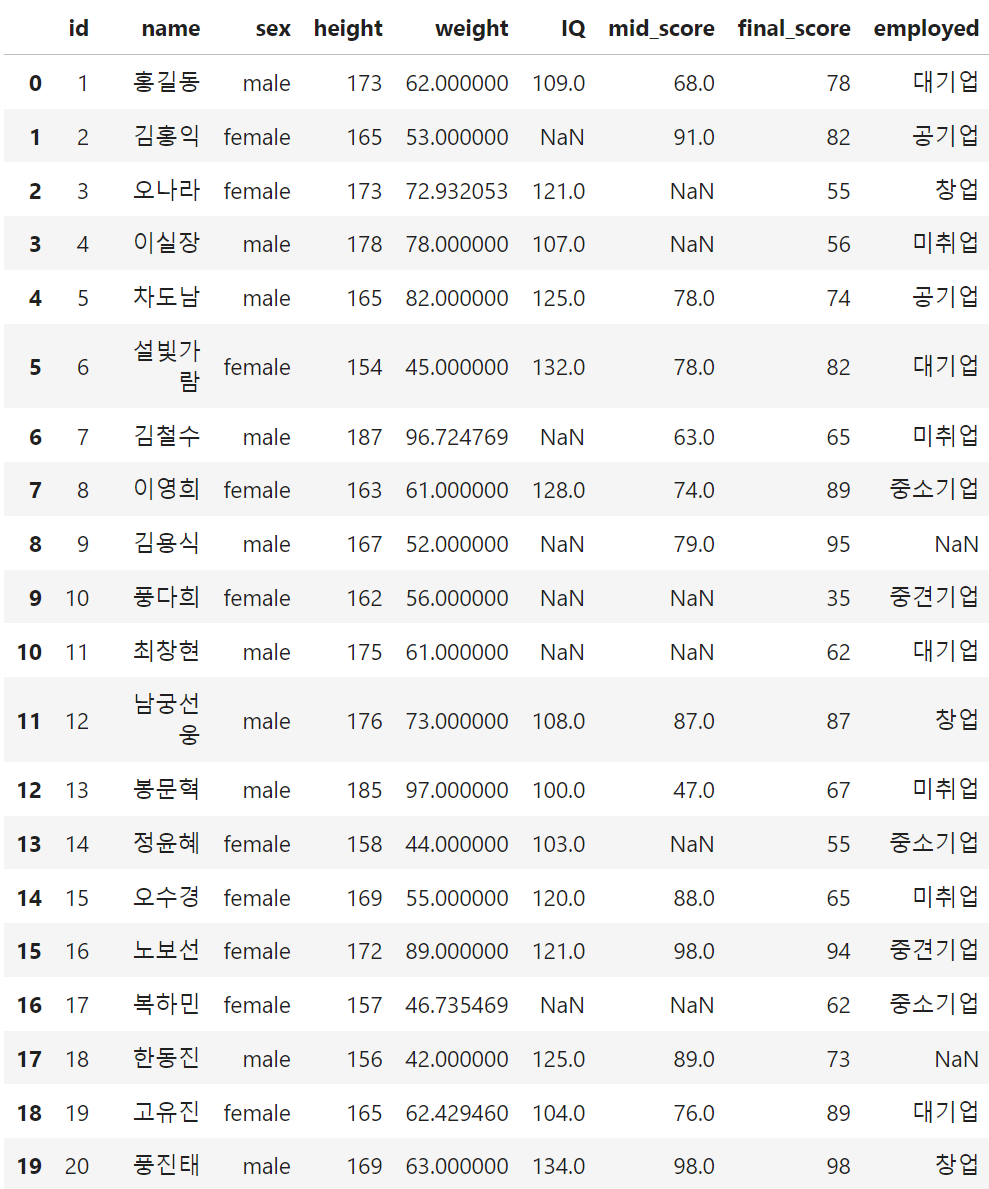
2.1.4 Hot-Deck Imputation
👉 연구중인 자료에서 표본을 바탕으로 비슷한 규칙을 찾아 결측치를 대체
👉 다른 변수에서 비슷한 값을 갖는 데이터 중에서 하나를 Random Sampling 하여 추출된 값으로 결측치 대체
👉 결측치가 포함된 변수가 가질 수 있는 값의 범위가 한정되어 있을 때 사용
👉 랜덤하게 가져온 값이기 때문에 어느정도 변동성을 더해준다는 점에서 표준오차의 정확도에 어느 정도 기여
🔥 한계
- 자료 분포를 가정하거나 모형을 정의하지 않고 결측치를 대체하므로 수리적으로 편향을 계산할 수 없어 대체 결과를 평가하기가 어려움
2.1.5 Cold-Deck Imputation
👉 외부 출처에서 비슷한 연구를 찾아 결측치 대체
👉 Hot-Deck Imputation과 유사하나 어떠한 규칙(ex) 비슷한 데이터 중에서 k번째 샘플의 값을 골라 대입 등)에 부합하는 하나의 값을 선정하여 결측치 대체
👉 비슷한 양상의 데이터 중에서 하나를 랜덤 샘플링하는 것이 아니라 직접 선정하여 대체한다는 점이 Hot-Deck과의 차이점
2.2 다중대치법 (Multiple Imputation)
👉 Single Imputation을 거친 여러 개의 데이터 셋을 만들고 이를 종합하여 평가하는 방법
👉 이미 관측된 값들은 여러 개의 데이터 셋을 만들어도 변함이 없기에, 동일한 값이 많이 나온 것처럼 평가되어 높은 가중치를 가짐. 그러나 결측치를 대체한 값은 만들어질 때마다 추가해주는 잔차의 변동으로 인해 관측값보다 상대적으로 약한 계수 추정 신뢰도를 갖게됨.
👉 데이터의 결측치가 MAR 일 때 사용 가능
👉 결측치의 불확실성 측면에서 Single Imputation보다 우수
📌 다중 대치법 3단계
1) Imputation step : 자료의 분포를 토대로 결측치를 대체하여 복수의 데이터 세트 생성
2) Analysis step : 생성된 복수의 데이터 세트를 분석(각 데이터 세트의 모수 추정치와 표본오차 계산)
3) Pooling step : Analysis 단계에서 분석한 모수 추정치와 표본오차를 바탕으로 데이터 세트를 하나로 합쳐 대체값 생성
2.2.1 MICE (Multiple Imputation by Chained Equations)
👉 n번의 결측치 대체를 통한 n개의 완전한 자료를 만들어 분석하는 방법
👉 연쇄방정식(Chained Equation) 방법은 Continuous, Binary, Categorical, Survey Skip Pattern 등에서도 적용할 수 있기 때문에 매우 유연한 방법
👉 결측치를 회귀방식으로 처리하기 때문에 수치형 변수에 자주 사용
💻 코드 예시
- Scikit-learn의 IterativeImputer Class
- max_iter : 결측치가 포함된 변수 각각에 단순대치법을 시행하는 round를 최대 몇 번까지 실시할 것인지를 결정, default=10
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
imputer_mice = IterativeImputer(max_iter = 10)
numeric_data = imputer_mice.fit_transform(numeric_data)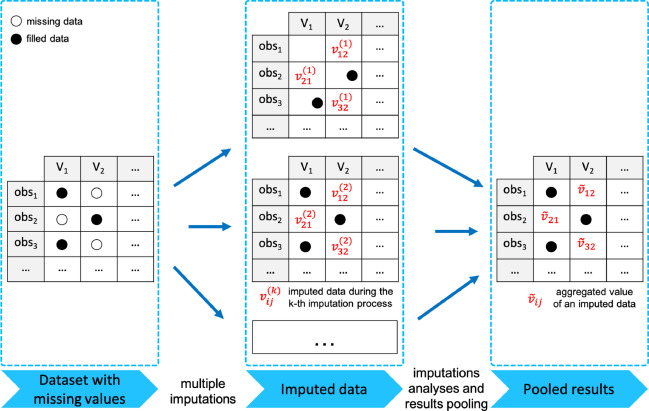
2.2.2 K-Nearest Neighbor(KNN) Imputation
👉 K-NN은 분석대상을 중심으로 가장 가까운 k개의 요소들 중에서 가장 많은 수의 집단으로 분류하는 지도학습 알고리즘
👉 결측치가 범주형이면 이웃 데이터 중 최빈값으로 대체하고, 연속형이면 이웃 데이터들의 중앙값으로 대체하는 방법
🔥 단점
- Outlier에 민감
- 적절한 k값 선택 필요
💻 코드 예시
- Scikit-learn의 KNNImputer Class
- n_neighbors : 몇 개의 이웃을 사용할지 지정, default=5
- weights : 가중치 설정, default='uniform'
from sklearn.impute import KNNImputer
knn = KNNImputer(n_neighbor=2, weights='uniform')
data = knn.fit_transform(data)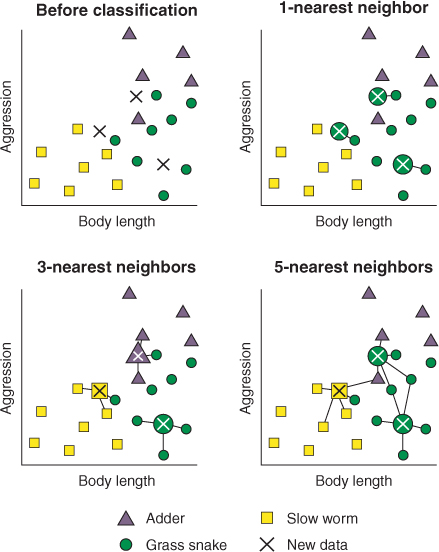
2.2.3 Deep Learning used Imputation
👉 범주형이나 숫자가 아닌 자료형에 효과적인 결측치 대체 방법
👉 DNN(Deep Neutral Network)을 이용하여 데이터의 결측치를 유추하여 대체
💻 코드 예시
import datawig
df_train, df_test = datawig.utils.random_split(train)
#Initialize a SimpleImputer model
imputer = datawig.SimpleImputer(
input_columns=['1','2','3','4','5','6','7', 'target'], # column(s) containing information about the column we want to impute
output_column= '0', # the column we'd like to impute values for
output_path = 'imputer_model' # stores model data and metrics
)
#Fit an imputer model on the train data
imputer.fit(train_df=df_train, num_epochs=50)
#Impute missing values and return original dataframe with predictions
imputed = imputer.predict(df_test)
📋 Reference
https://daebaq27.tistory.com/43
https://blog.naver.com/tkdgus4u/222548791626