[ML] 의사결정나무(Decision Tree)

양승웅·2024년 1월 11일

Machine Learning

목록 보기

1/4

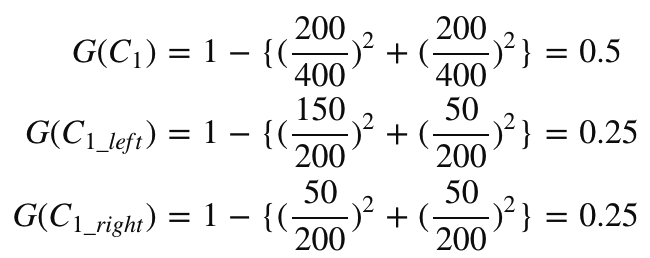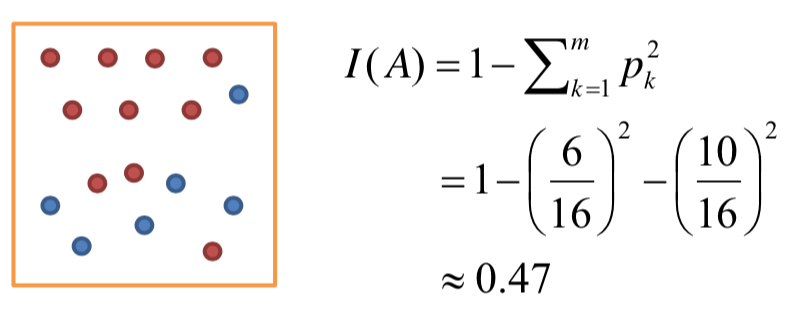
📢 개요

✏️ 의사결정나무(Decision Tree)란?

👉 뿌리(root)에서 시작하여 각 분기점(node)에서 특정 기준에 따라 데이터를 나누고, 마지막에는 각각의 잎 노드(leaf node)로 데이터를 분류하는 모형
👉 독립변수의 조건에 따라 종속 변수의 값을 예측하는 데 사용되는 모형
👉 불순도(impurity)를 최소화 하는 방향으로 데이터를 분류해나가는 것이 핵심 원리

⭐ 장점
👉 별도의 표준화 전처리 과정이 요구되지 않음

📌 용어 정리

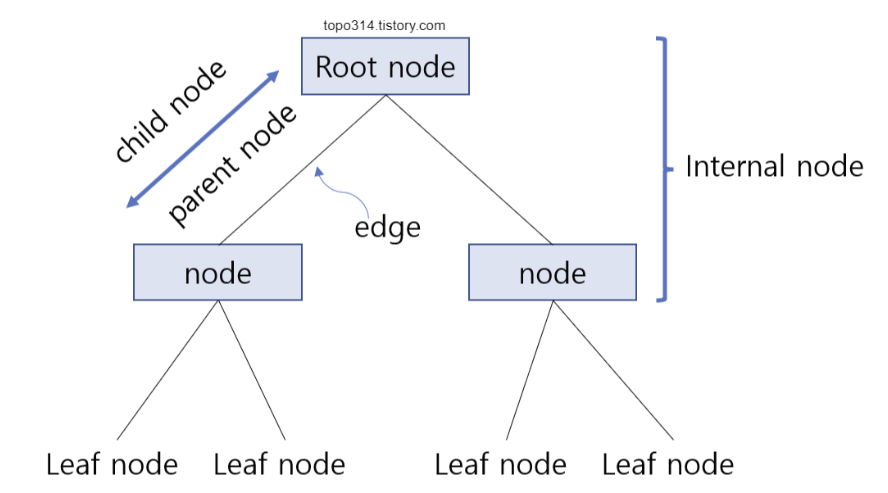
뿌리마디(root node) : 시작되는 마디로 전체 자료를 포함

자식마디(child node) : 하나의 마디로부터 분리되어 나간 2개 이상의 마디들

부모마디(parent node) : 주어진 마디의 상위마디

끝마디(terminal node) : child node가 없는 마디

중간마디(internal node) : parent node와 child node가 모두 있는 마디

가지(branch) : root node로부터 terminal node까지 연결된 마디들

깊이(depth) : root node로부터 terminal node까지의 internal nodes의 수

🔎 절차

🧩 STEP#1. 성장(Tree Growing)
👉 최대 크기의 tree model 형성
👉 각 마디에서 적절한 최적의 분리규칙을 찾아서 tree를 성장시키는 과정으로서 적절한 정지규칙을 만족하면 중단

🧩 STEP#2. 가지치기(Pruning)
👉 최대 크기의 tree model에서 불필요한 가지를 제거하여 부분나무모형(subtrees)의 집합을 탐색
👉 Decision Tree에 가지가 너무 많을 경우, 이는 데이터가 과대적합 된 것이며 이러한 문제를 차단하기 위한 전략으로 적용되는 기법

📌 가지치기 방법

max_depth parameter를 통해 최대 깊이를 지정

min_sample_split parameter를 통해 한 node에 들어있는 데이터의 최소 개수를 지정

🧩 STEP#3. 최적의 tree model 선택
👉 가지치기의 결과인 tree model의 집합에서 최적의 model을 선택
👉 검증오차가 가장 작은 Decision Tree를 평가

🧩 STEP#4. 해석 및 예측
👉 구축된 tree model을 해석하고 예측모형을 설정한 후 예측에 적용

📚 분류기준(Split Criterion)

👉 Decision Tree 모형에서는 클래스를 정확하게 구분해줄 수 있는 분류기준을 찾는것이 중요함
👉 현재 집단에 어느 정도 다른 객체들이 섞여있는지 확인하고 불순도가 낮은 쪽으로 가지를 형성해나가게 되는데, 이 때 사용되는 것이 불순도(Impurity) 알고리즘
👉 불순도(Impurity)를 측정하는 방법으로는 지니계수(Gini Index), 엔트로피(Entropy), log_loss 크게 2가지가 존재

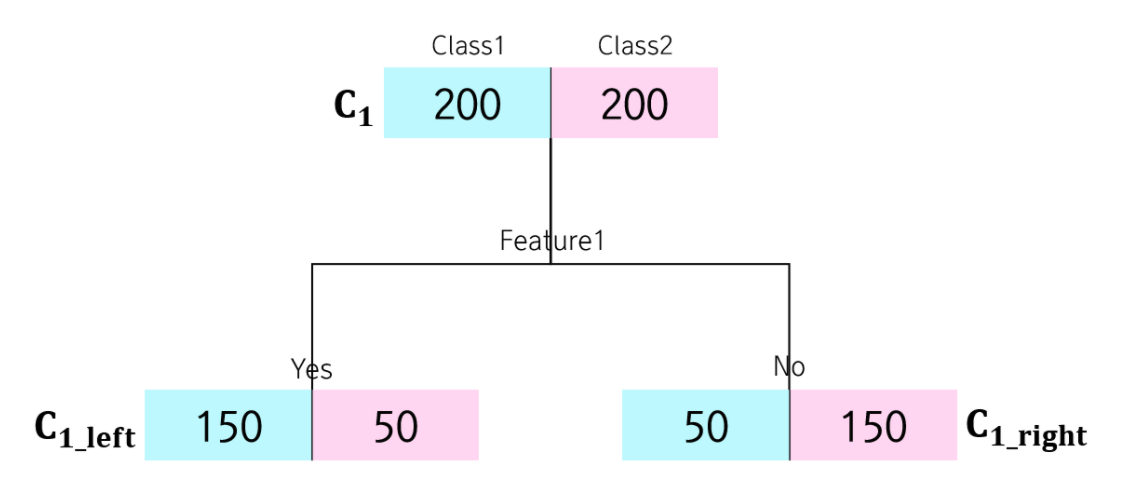
1. 지니 계수(Gini Index)

\boxed{G(A) = 1- \sum_{j=1}^n p_j^2}

👉 통계적 분산정도를 정량화해서 표현한 값
👉 0과 1사이의 값을 가지며, 한 집단 내의 데이터들의 특성이 동일해질 수록 지니계수는 낮아지고, 다양한 특성의 데이터들이 혼재되어 있을 수록 지니계수는 높아짐
👉 '0'은 완벽하게 분류된 불확실성이 0인 상태를 의미하며, '1'은 모든 클래스가 동등하게 분포된 상태를 의미

📌 참고

2. 엔트로피(Entropy)

\boxed{E = \sum_{i=1}^k -p_i \times log_2(p_i)}

👉 데이터의 복잡도를 측정하는 척도
👉 엔트로피가 높을수록 불순도가 높은 것이며, 낮을수록 불순도가 낮은 것
👉 엔트로피가 1이면 불순도가 최대이며 한 범주 안에 서로 다른 데이터가 정확히 반반이 존재하는 것이며, 0이면 불순도가 최소이며 한 범주 안에 하나의 데이터만 존재한다는 의미
👉 Decision Tree는 반응변수가 잘 구분이 될 수 있도록, 즉 엔트로피가 낮아지는 방향으로 분리해주어야 함

📙 정보이득(Information Gain)

Information Gain(F) = Entropy(S_1) - Entropy(S_2)

👉 하나의 변수 F를 기준으로 root node에서 다음 node로의 분할이 이루어졌을 경우, 분할 전(S1)과 분할 후(S2)의 엔트로피 차이 값을 정보이득으로 정의
👉 어떤 변수로 분할 했을 떄 계산되는 불확실성의 차이
👉 Decision Tree는 정보이득 값이 최대가 되는 변수를 기준으로 node를 분할함

❓ 만약,
어떠한 변수를 기준으로 다음 단계로 분할 한 후의 엔트로피(S2)가 크다?
$\implies$ 여전히 불순도가 높다!(정보이득 低) = 클래스 간 분리가 확실하게 이루어지지 않았다

반대로, 다음 단계로 분할 한 후의 엔트로피(S2)가 작다?
$\implies$ 불순도가 낮다!(정보이득 大) = 클래스 간 분리가 어느정도 확실하게 이루어졌다

$\therefore$ 정보이득 값이 크면 그 변수를 분할 기준 변수로 사용한 것이 적절하다는 것!

📗 특성 중요도(Feature Importance)

👉 Tree가 만들어지는 과정에서 각 특성(feature)이 얼마나 중요한지를 평가하는 것으로 불순도를 감소하는데 기여한 정도를 나타내는 값
👉 0과 1 사이의 값을 가지며 각 특성에 대해 0은 전혀 사용되지 않았다는 의미이고, 1은 완벽하게 정답(target)을 예측하였다는 의미

❓ 만약,
🧩 특성 중요도가 높다?
$\implies$ Tree에서 높은 층에 해당하는 node에서 질문으로 사용되는 특성이다!

🧩 특성 중요도가 낮다?
$\implies$ Tree에서 낮은 층에 해당하는, 세세하게 클래스를 분류하는 node에서 질문으로 사용되는 특성이다!
$\implies$ 혹은, 질문에 사용되지 않는 특성이다!

🧩 특성 중요도가 1의 값을 갖는 특성이 있다?
$\implies$ 모델이 정답(target)을 예측하는 데 다른 특성은 전혀 고려하지 않는다!

🙏 Reference

https://diseny.tistory.com/entry/%EC%9D%98%EC%82%AC%EA%B2%B0%EC%A0%95%EB%82%98%EB%AC%B4decision-tree
https://huidea.tistory.com/273
https://kolikim.tistory.com/22
https://wanttosleep1111.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-Decision-Tree-%EA%B5%90%EC%B0%A8-%EA%B2%80%EC%A6%9D-%ED%8A%B9%EC%84%B1-%EC%84%A0%ED%83%9D

양승웅

다음 포스트