Transformer[Attention Is All You Need]

김대현·2021년 11월 7일

0. Introduction

Transformer는 Google Brain팀에서 2017년에 발표한 논문으로 NLP분야 뿐만 아니라 최근엔 Computer vision 분야에서도 엄청난 영향력을 발휘하고 있습니다. Transforemr의 주요 특징으로는 다음과 같습니다.

오로지 Attention mechanisms에 기반을 두었다. 즉 RNN과 CNN을 완전히 배제하였디.
병렬화 처리를 가능하게 했다.
Positional Encoding을 사용해 Sequential 위치 정보를 보존했다.

이번 Transfomer 설명은 다음과 같은 구성으로 진행될 것입니다.

1. Transformer model의 전반적인 Architecture

2. Self-Attentnion

3. Encoder, Decoder

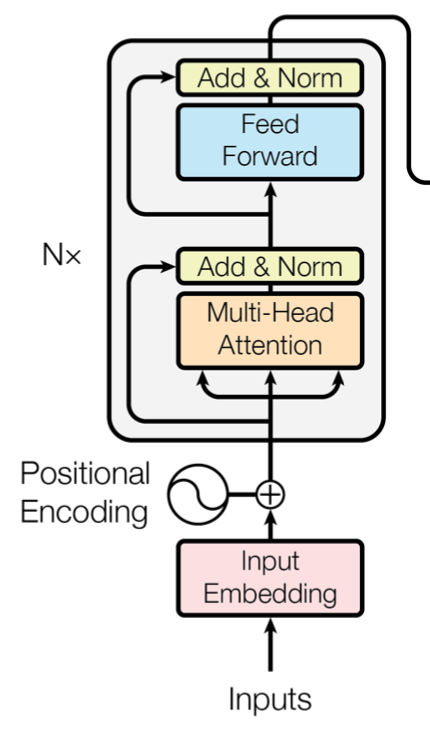
1. Transformer Architecture

Transformer는 아래 그림과 같이 encoder와 decoder로 구성되어 있습니다. encoder는 2개의 sub layer, decoder는 3개의 sub layer로 구성되어져 있습니다.

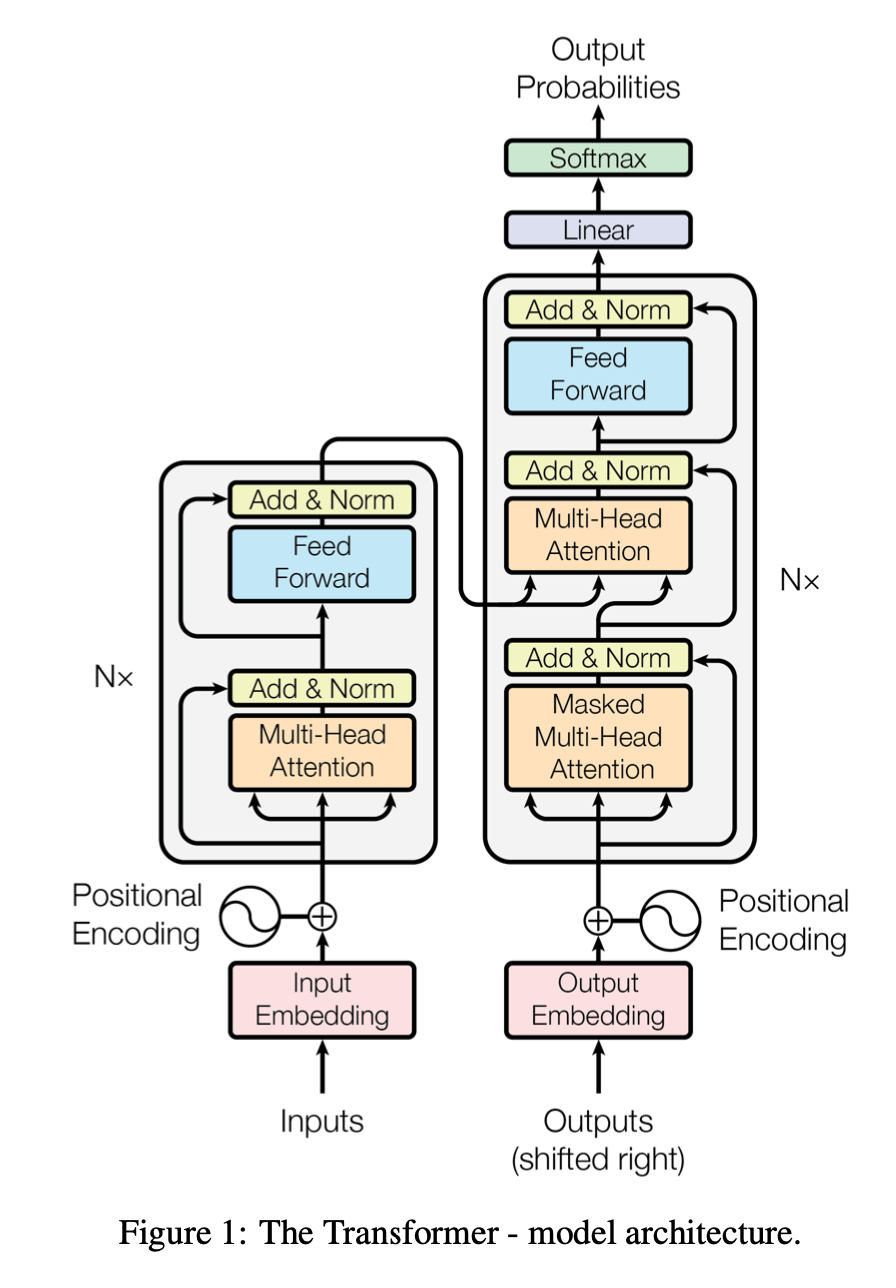
[출처] : https://arxiv.org/abs/1706.03762

또한 아래 그림과 같이 encoder와 decoder모두 각 sub layer를 총 6번 거치게 되도록 쌓여져 있습니다.

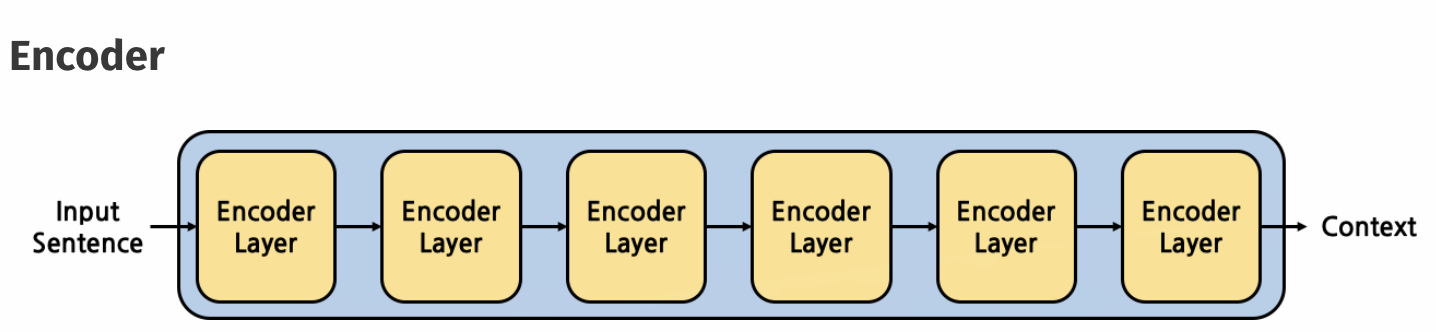
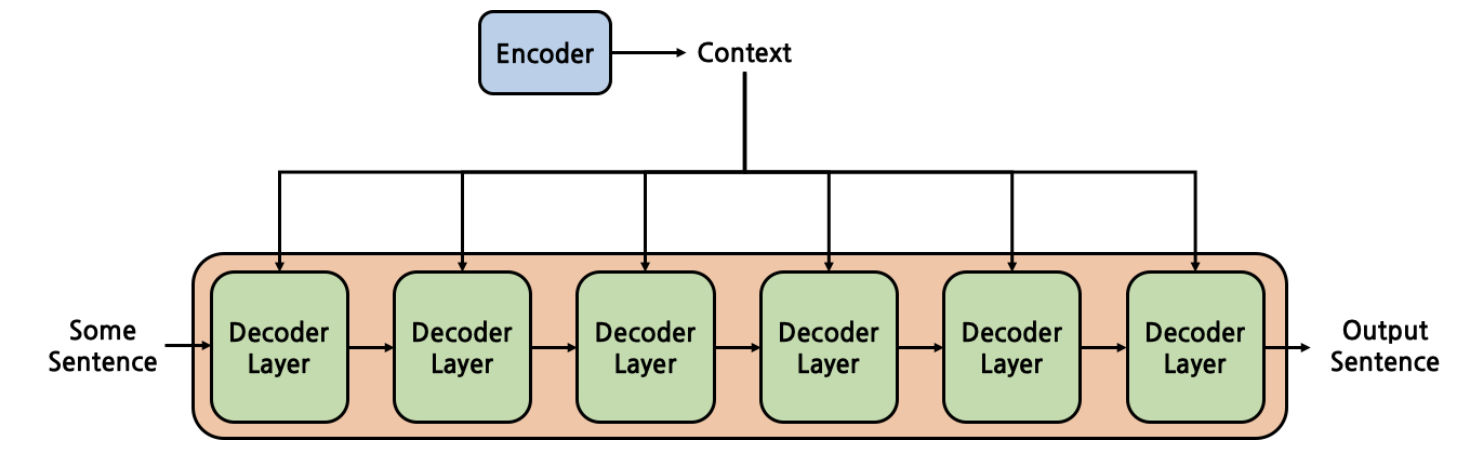
[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

입력 부분에는 input Embedding에 Positional Encoding 값을 더한 값이 모두 각각 Encoder와 Decoder에 들어가게 되는데 이는 서두에 언급했다 싶이 Transformer는 RNN을 배제했기 떄문에 Attention만으로는 위치 정보를 포함하고 있지 않습니다.

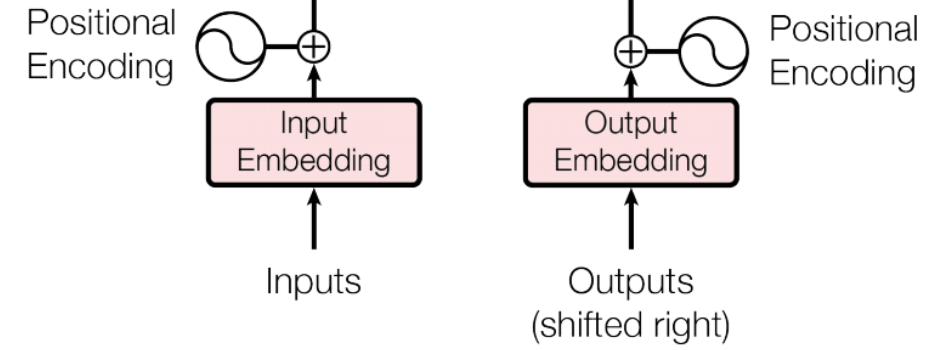
따라서 Transformer는 Positional Encoding을 사용함으로서 위치 정보를 포함시켰습니다.

2. Self-Attention

Transformer에 가장 핵심적인 부분이 바로 이 부분입니다. 자세하게 하나하나 설명하겠습니다.

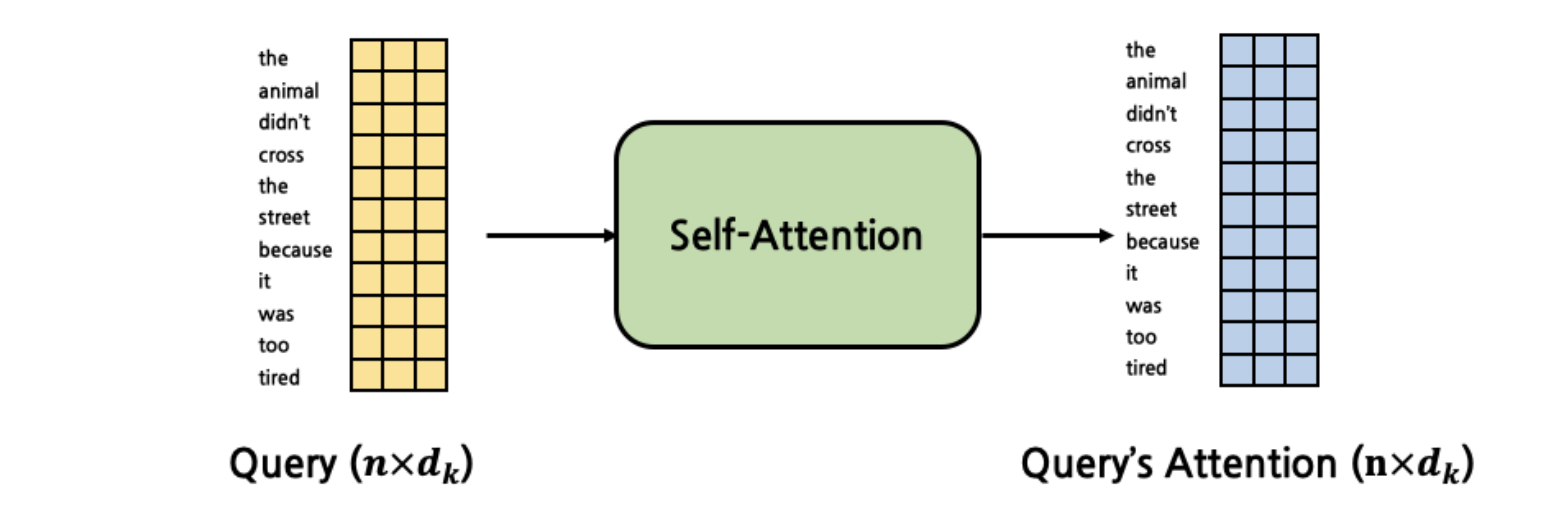
Positional Encoding까지 한 input은 Multi-head attention layer로 들어가게 되는데 아래 그림과 같이 Scaled Dot-Product Attention을 하게됩니다.

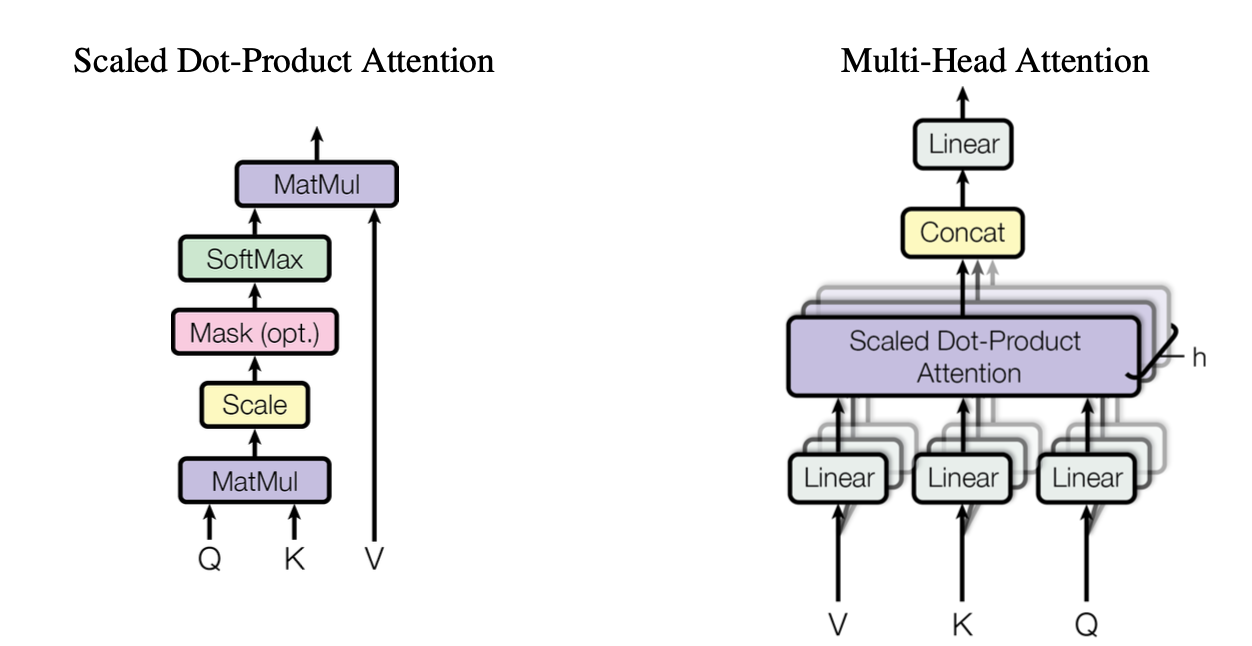
[출처]: https://arxiv.org/abs/1706.03762

우선 Scaled Dot-Product Attentiong하기 전에 Linear층을 통과하게 되는데 이를 통과하므로서 Q,K,V는 모두 동일한 차원으로 Projection이 됩니다.

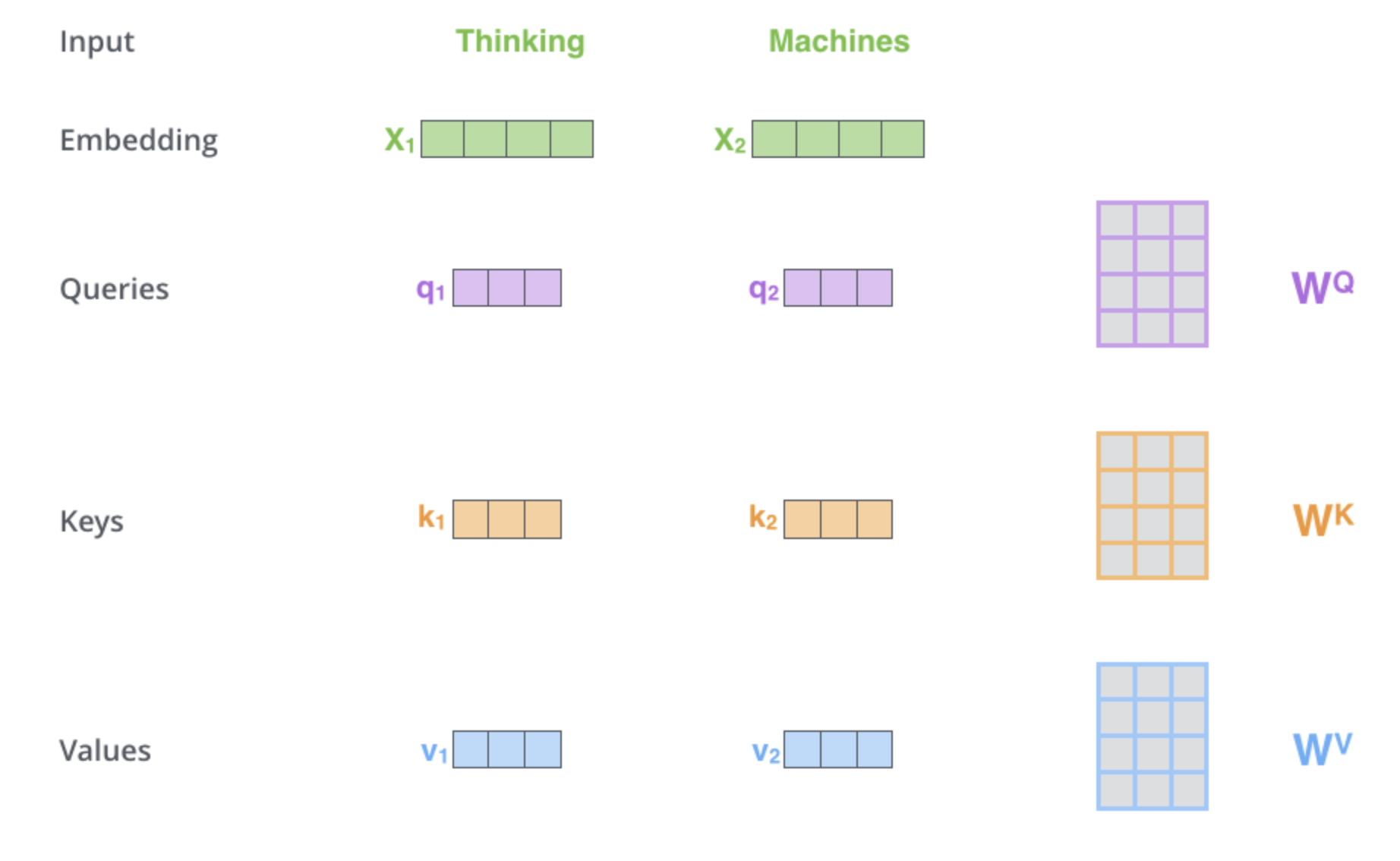
[출처]:https://jalammar.github.io/illustrated-transformer/

이때의 각 Q,K,V의 차원을 $d_k=3$ 이라고 하겠습니다. 여기서 Q,K,V가 모두 동일한 차원인 이유는 Self라는 의미를 다시 되짚어 봐야하는데 결국에는 동일한 문장내에 있는 다른 단어(Token)들과의 Attention score를 구하는 것이기 때문 에 Q,K,V는 모두 동일한 차원일 수밖에 없습니다. 왜냐하면 애초에 같은 문장내에 같은 Token을 projection하기 때문입니다. 여기서 Q,K,V는 다음과 같은 의미를 가지고 있습니다.

Query: Context,즉 현재 시점의 token
Key: Query에 반응하여 Attention을 구하고자 하는 대상
Value: attention을 구하고자 하는 대상 token을 의미 (Key와 동일한 token)

Q,K,V의 의미를 알았으니 실제 Attention을 구해봅시다.

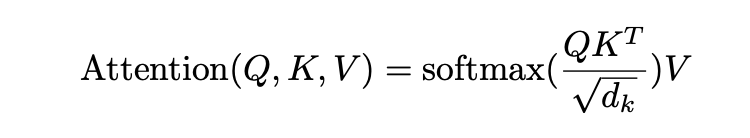
Attention는 위와 같이 구해지는데 그림을 통해서 설명을 하겠습니다.

Q,K,V가 모두 Linear 연산을 통해 모두 동일한 차원으로 임베딩이 되었다고 하고 이떄의 차원을 $d_k=3$ 이라고 하겠습니다.

[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

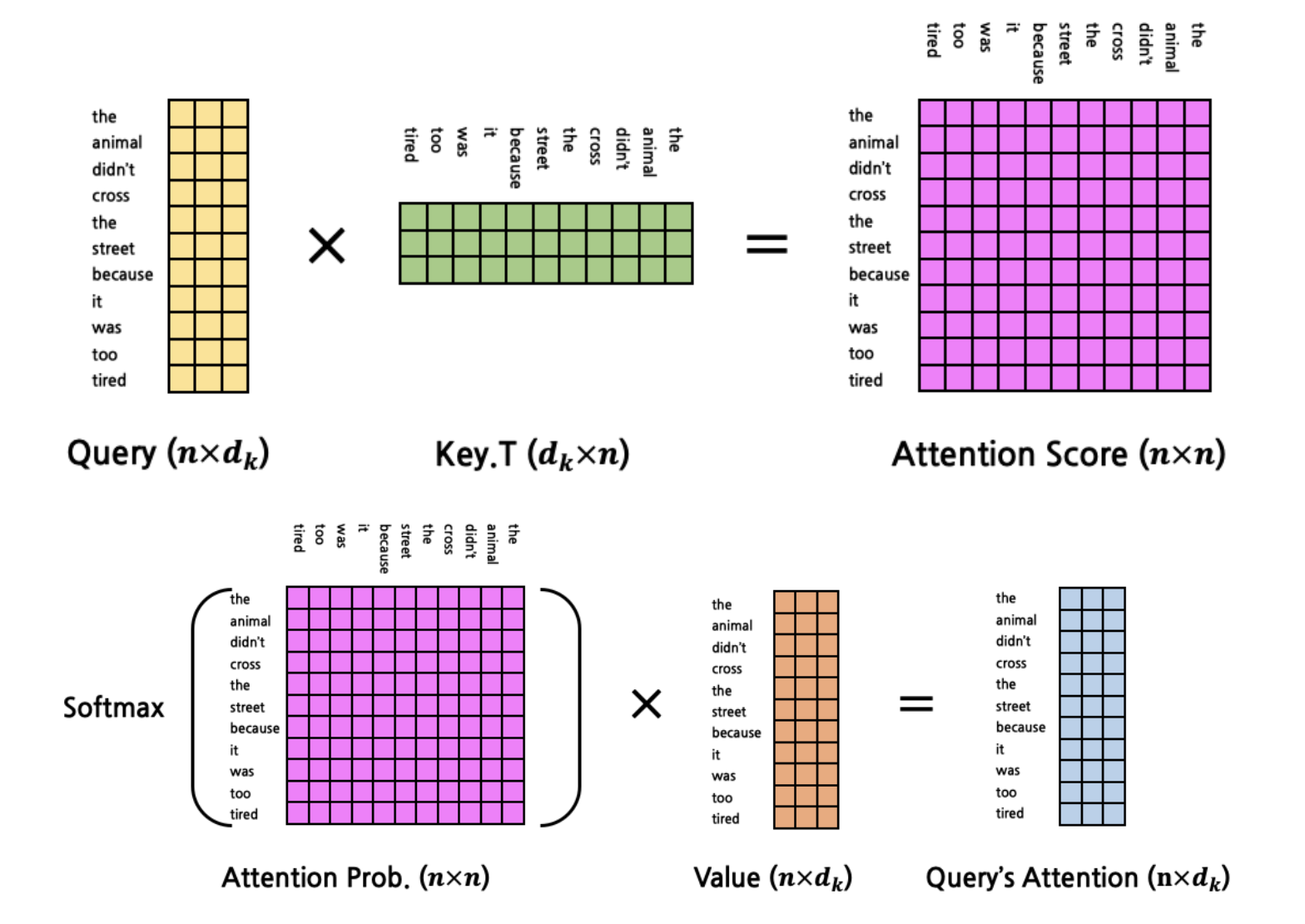
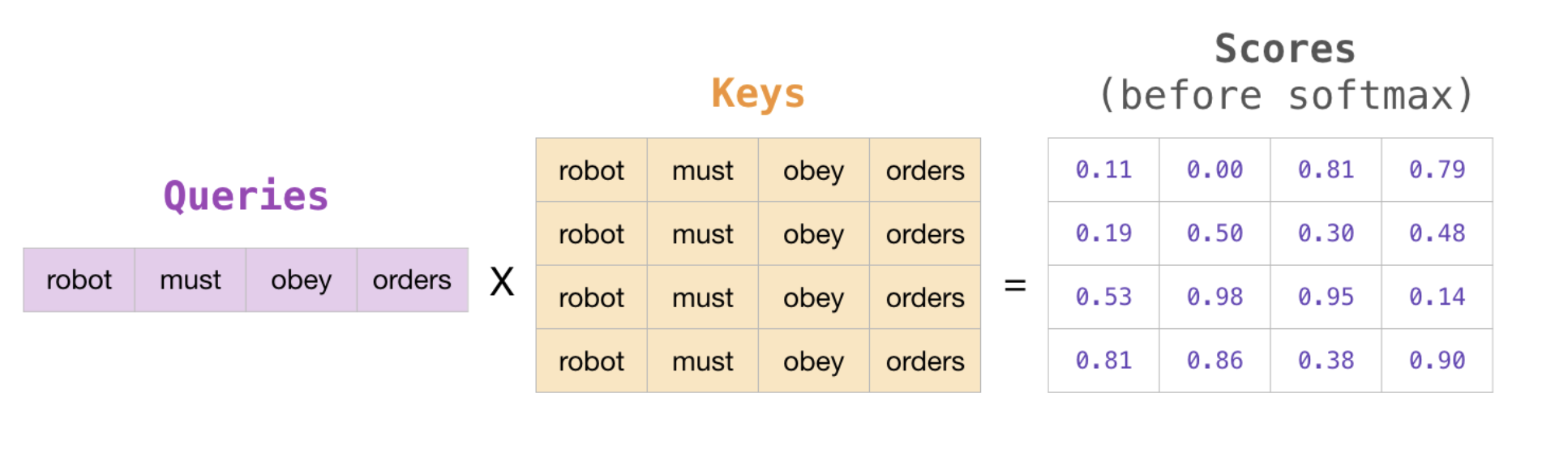
위의 수식대로 우선 Q하고 K를 곱합니다.

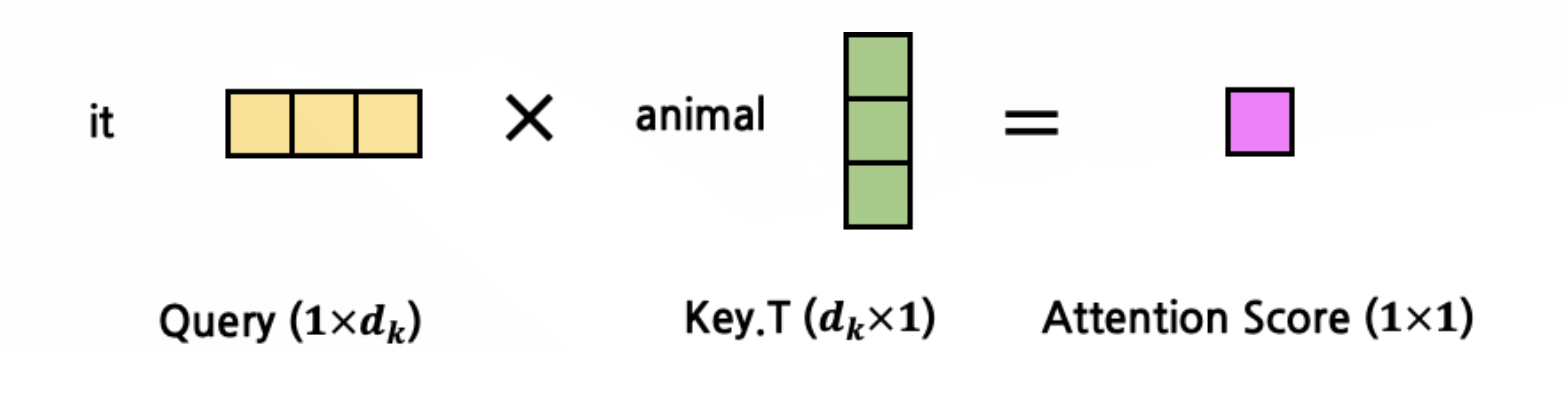
[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

곱한다는 의미는 Q와 K의 관계, 즉 attention score를 구한다는 것입니다. 그렇다면 여기서 Q와 다른 K와의 관계를 구하기 위해 K를 확장하겠습니다.

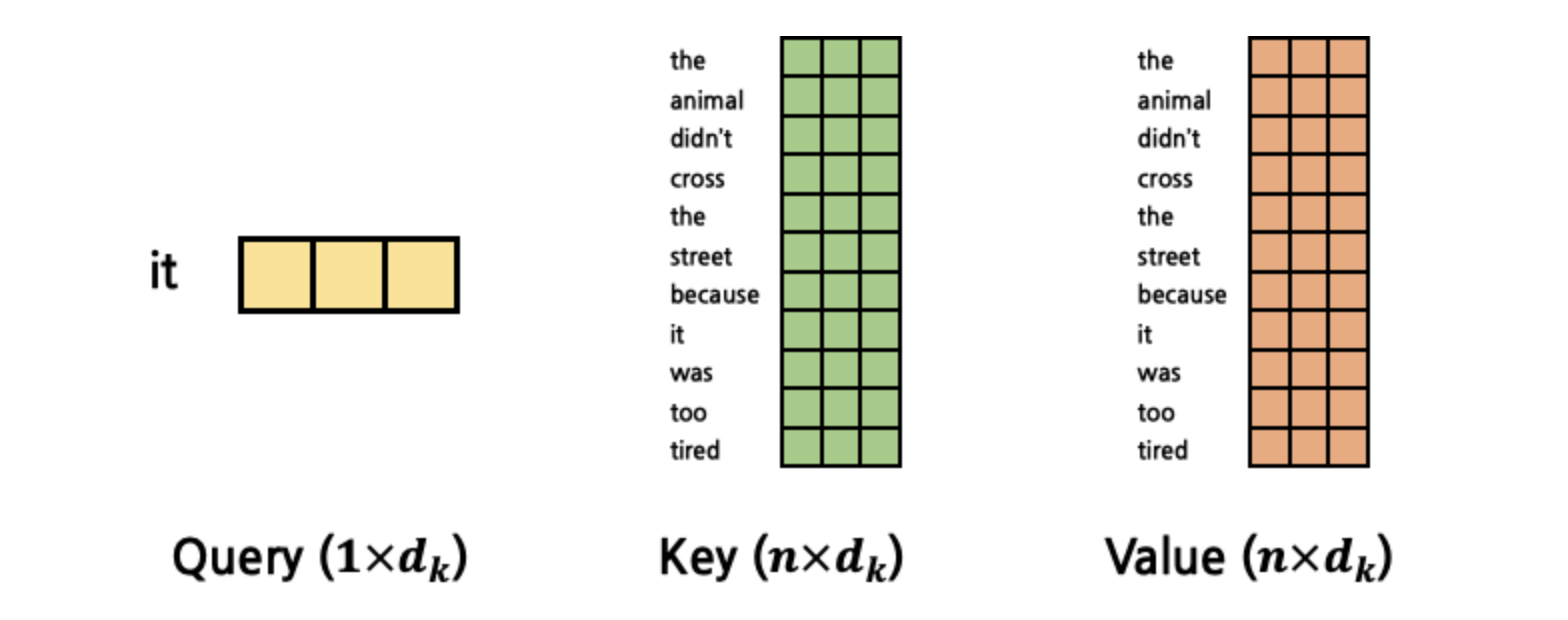
[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

그렇다면 아래와 같이 'it'이라는 단어와 나머지 단어들 사이의 관계(attention score)가 구해집니다.

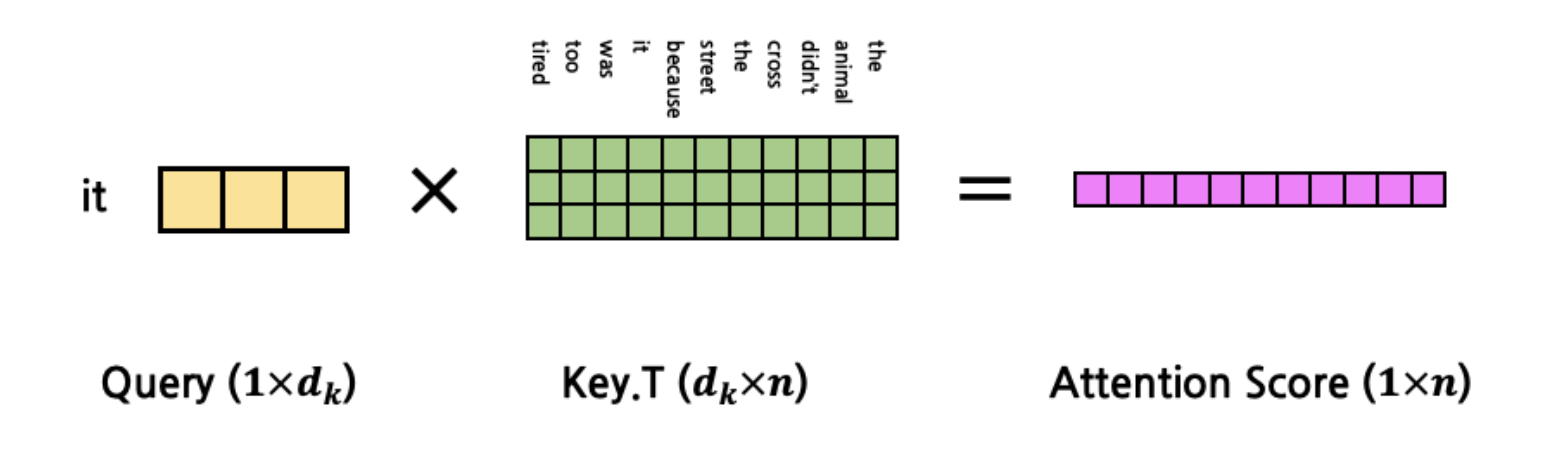
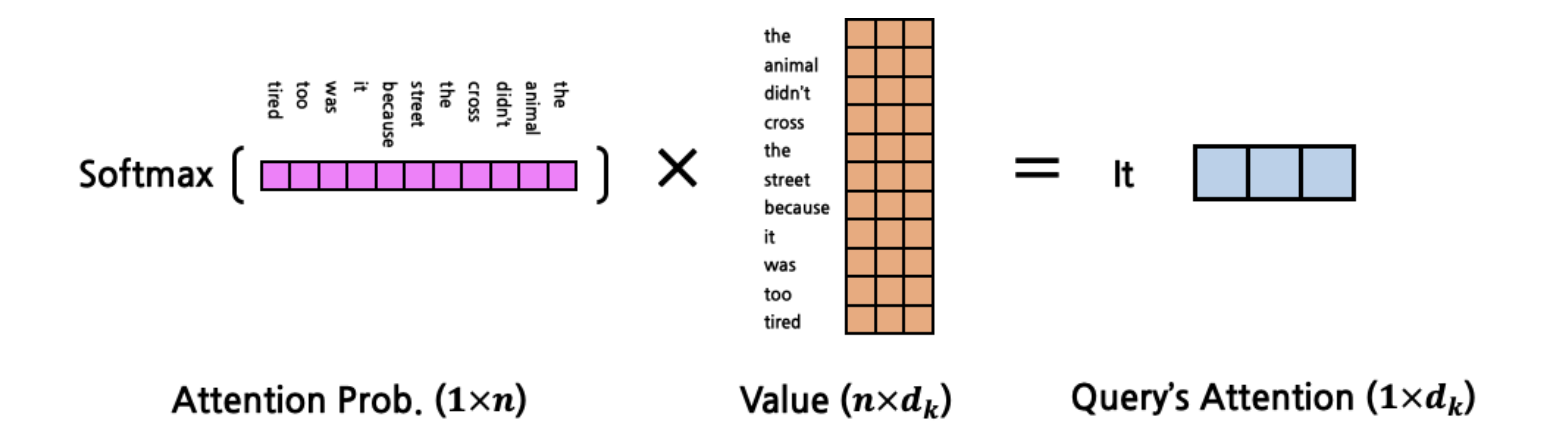
[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

이때 행렬 곱을 단순히 했을때 크기가 커지면 'overflow'나 'small gradient'문제가 발생되기 때문에 자기 자신의 차원의 루트 값으로 나눠줍니다. 이것 떄문에 단순히 Dot-Product이라는 용어에 Scaled이라는 의미가 추가됩니다. 즉 값을 모두 표준화 시키겠다는 의미입니다.

$z = \frac{x-u}{\sigma}$

표준화 공식은 위와 같고 근사적으로

$\frac{Q\cdot K}{\sqrt{d_k}} = \frac{Q\cdot K}{\sigma}$

같다는 수학적 증명이 있습니다. 그렇다면 여기서 더 나아가서 한 개의 Query가 아니라 문장 내에 있는 모든 Token을 Query로 만들어서 Attention score를 계산할 수도 있습니다.

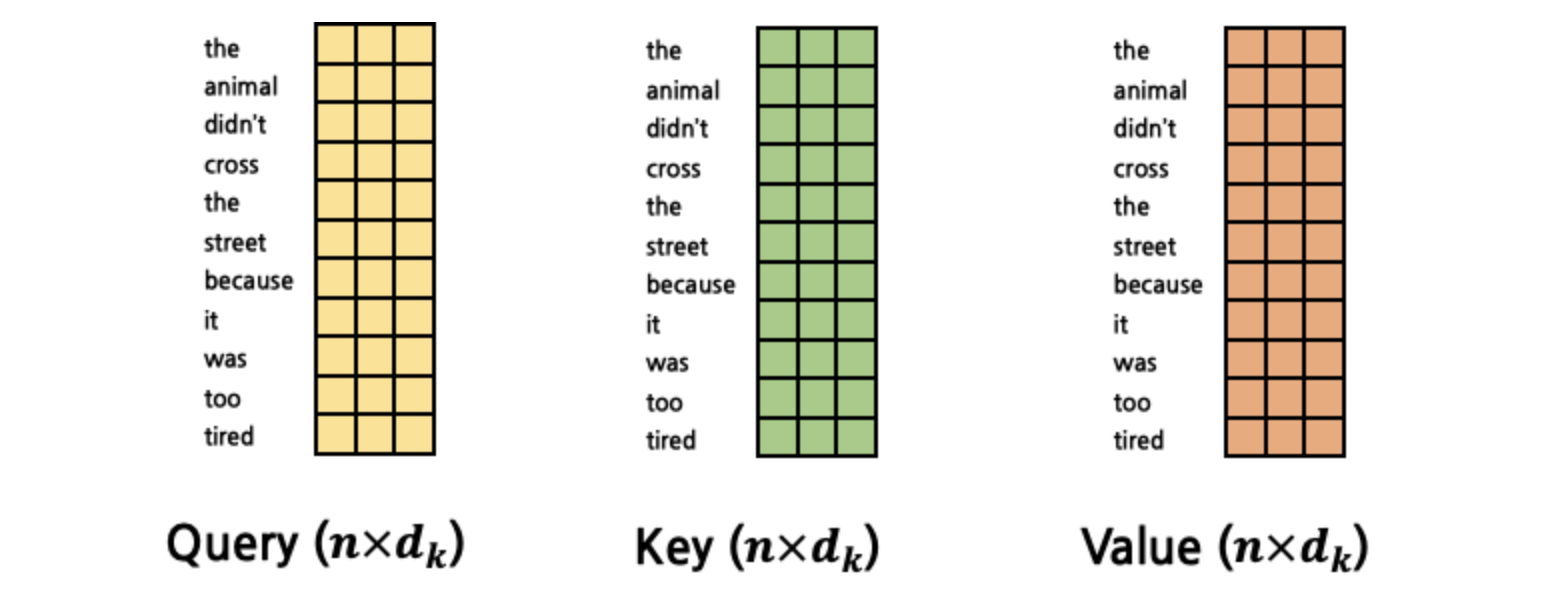
[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

위의 결과가 같이 결국에는 최종 Attention값의 차원은 input과 같게 됨을 알 수 있습니다.

[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

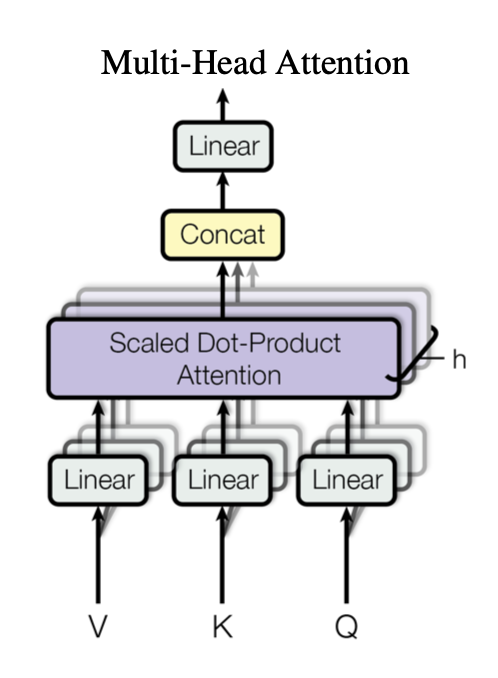
이제 여기서 더 확장을 해보자. 논문에서는 Multi-head attention이라고 명명하였고 head의 개수를 8개로 설정하였다.

[출처]: https://arxiv.org/abs/1706.03762

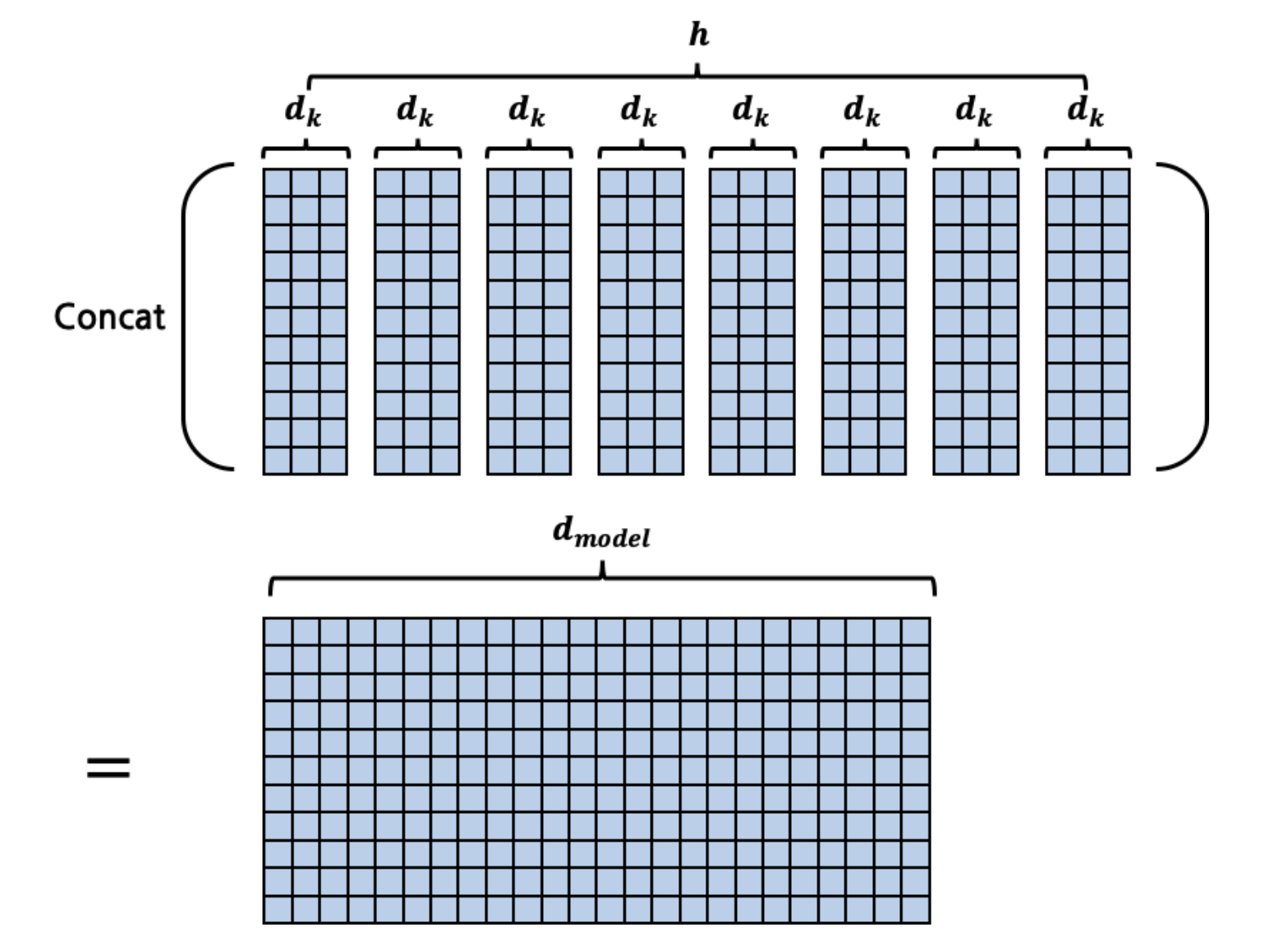
Transformer는 Scaled Dot Attention을 한 Encoder Layer마다 1회씩 수행하는 것이 아니라 h회 수행한 뒤, 그 결과를 종합해 사용한다. 한 개의 Attention을 반영하는 것 보다는 여러가지 Attention을 종합적으로 반영하는 것이 결과에 더 좋기 때문이다. 하지만 Scaled Dot Attentiond을 h회를 수행하는 건 너무나 계산적으로 비효율적이다. 우리는 행렬을 사용하는 법을 익히 알고 있기 때문에 애초에 input의 차원 자체를 8회 수행에 맞게끔 늘리는 것이다. 즉 새로운 차원을 $d_{model}$ 이라고 한다면 $d_{model} = h * d_k$ 가 된다. 그림으로 표현하면 다음과 같다.

[출처] : https://cpm0722.github.io/pytorch-implementation/transformer

이렇게 한 덩어리의 $d_{model}$ 단위로 위의 Scaled dot-product를 수행하는 것이다. 최종적인 Multi-head attetion layer의 input와 Output은 다음과 같다.

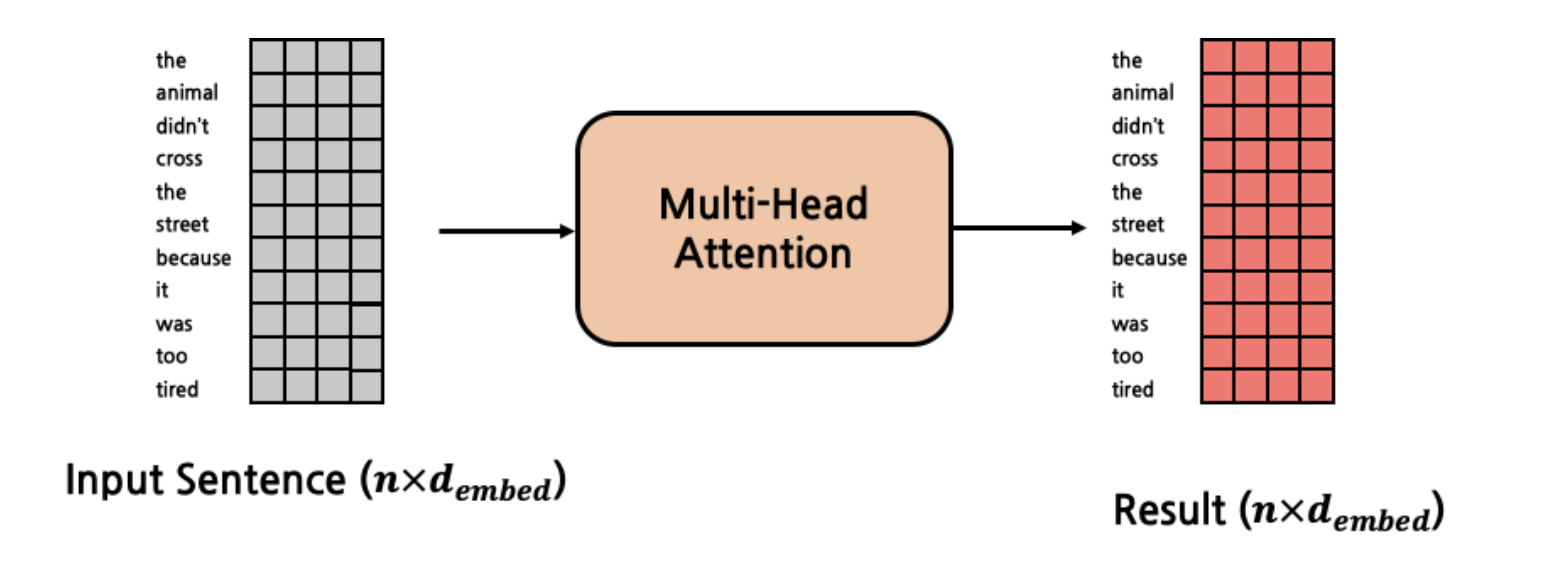
코드로 살펴보면 다음과 같이 나타낼 수 있다.


def cal_attention(q, k, v, d_k, mask=None, dropout=None):
    
    scores = torch.matmul(q, k.transpose(-2, -1)) /  math.sqrt(d_k)
    
    if mask is not None:
        
        scores = scores + mask
    
    scores = F.softmax(scores, dim=-1)
    
    if dropout is not None:
        scores = dropout(scores)
        
    output = torch.matmul(scores, v)

    return output


class MultiHeadAttention(nn.Module):
    def __init__(self, hid_dim, n_heads):
        super().__init__()
        
        assert hid_dim % n_heads == 0
        
        self.hid_dim = hid_dim # 768
        self.n_heads = n_heads # 12
        self.head_dim = hid_dim // n_heads ## 64
        
        self.query = nn.Linear(hid_dim, hid_dim)
        self.key = nn.Linear(hid_dim, hid_dim)
        self.value = nn.Linear(hid_dim, hid_dim)

        self.dropout = nn.Dropout(0.1)
                
    def forward(self,hidden_states,attention_mask = None):  


        # 변수 설명 
        # hidden_states : BertEmbedding output [2, 9, 784] [Batch size, Max_sequence_length,model size ]
        # self.n_heads : multi-head attention에서의 head의 개수 여기서는 head수가 12 
        # self.head_dim : 하나의 임베딩된 벡터의 차원 여기서는 64이다.
        # self.hid_dim : model size를 의미 정확히 말하면 n_heads(헤드수 ) * head_dim(하나의 임베딩된 벡터의 차원) 
        # 의미 : Q, K, V 자체를 n(batch size) x head_dim가 아닌, n× hid_dim로 생성해내서 한 번의 Self-Attention 계산으로 n× hid_dim의 output을 만들어내게 된다.
        # 때문에 Q, K, V를 생성해내기 위한 dembed×head_dim의 weight matrix를 갖는 FC layer를 3∗h개 운용할 필요 없이  hid_dim× hid_dim의 weight matrix를 갖는 FC layer를 3개만 운용하면 된다.


        bs = hidden_states.size(0) # batch size를 얻는다.


        # Step 1
        #  Input vector로부터 Query, Key, Value vector 생성 
        # 그리고 shape를 모두 동일하게 [batch size,max_sequence_length,n_heads,head_dim]으로 통일한다.
        q = self.query(hidden_states).view(bs, -1, self.n_heads, self.head_dim)
        k = self.key(hidden_states).view(bs, -1, self.n_heads, self.head_dim)
        v = self.value(hidden_states).view(bs, -1, self.n_heads, self.head_dim)
        
        # attention score 계산을 위해 shape를 [batch size,n_heads,max_sequence_length,head_dim]로 변경시킨다.
        q = q.transpose(1,2) # q shape : torch.Size([2, 12, 9, 64])
        k = k.transpose(1,2) # k shape : torch.Size([2, 12, 9, 64])
        v = v.transpose(1,2) # v shape : torch.Size([2, 12, 9, 64])

        
        # Step 2. Query · Key (matrix product) 하여 계산
        # Step 3. Score를 Key vector 차원수의 제곱근으로 나눔
        # Step 4. Softmax 계산
        # Step 5. Value vector에 softmax score를 곱함
        # attention score를 계산한다.
        scores = cal_attention(q,k,v,self.head_dim, attention_mask, self.dropout)

        # Permute와 Reshape를 하여 최종적인 output size[batch size, max_sequence,hid_dim]으로 맞춘다.
        # concatenate heads and put through final linear layer
        concat = scores.transpose(1,2).contiguous().view(bs, -1, self.hid_dim)
        return concat

3. Encoder, Decoder

3-1. Encoder

[출처] : https://arxiv.org/abs/1706.03762

encoder는 2개의 sub layer(Multi-head attetnion과 Feed Forward(MLP)층으로 구성되어 있습니다. 그리고 각 층을 나온 결과에 Layer Normalization과 Residual connection을 하고 있습니다.

여기서 Layer Normalization과 Residual connection을 자세히 설명하지는 않겠습니다. 간단하게 Layer Normalization은 NLP와 같은 분야에서 사용하면 특히 Transformer와 같은 고속/병렬 연산이 주 특징인 곳에서는 더 좋은 성능을 낼 수 있다고 알려져있다고 이해하시면 됩니다. Residual connection의 경우 층이 깊어질수록 gradient vanishing 문제가 생겨서 오히려 test error가 더 커지는 문제를 방지 하고자 도입한 기법이라고 이해 하시면 되겠습니다.

Multi-head attention은 이미 설명했으므로 Position-wise Feed Forward Layer만 간단히 설명하겠습니다. 이 층은 단순하게 2개의 FC Layer를 갖는 Layer이고 Multi-head attention과 마찬가지로 input의 shape를 그대로 유지한다는 것이 특징입니다.

구현 코드는 다음과 같습니다.

class PositionwiseFeedforwardLayer(nn.Module):
    def __init__(self, hidden_dim, pf_dim, dropout_ratio):
        super().__init__()

        self.fc_1 = nn.Linear(hidden_dim, pf_dim)
        self.fc_2 = nn.Linear(pf_dim, hidden_dim)

        self.dropout = nn.Dropout(dropout_ratio)

    def forward(self, x):

        # x: [batch_size, seq_len, hidden_dim]

        x = self.dropout(torch.relu(self.fc_1(x)))

        # x: [batch_size, seq_len, pf_dim]

        x = self.fc_2(x)

        # x: [batch_size, seq_len, hidden_dim]

        return x

[소스 코드 출처] : https://colab.research.google.com/drive/1mt5G4MMneREGuQbaYYIfL_C1cvTTKIK1#scrollTo=0jn4VCWdXhK5

3-2. Decoder

decoder는 다음과 같이 구성이 되어있다.

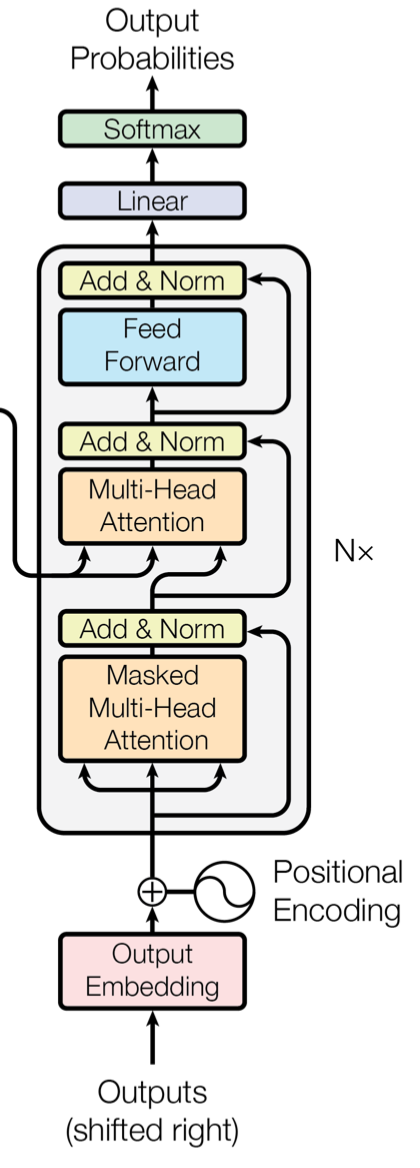
[출처]: https://arxiv.org/abs/1706.03762

주요 특징으로는 다음과 같다.

맨 아래의 Multi-head attetnion layer에서 mask를 사용하므로서 현재 시점 이후의 token에 대해서는 단어 예측에 사용하지 못하도록 mask를 씌운다.
2번째 multi-head attention 층에서 입력으로 들어오는 Q값은 바로 아래층의결과 값이고 K,V는 encoder층에서 최종 결과값들이다.

1번을 설명하자면 다음과 같다.

아래 그림을 보면 현재 시점 이후의 token들은 모두 mask를 써서 다음 값의 예측에 사용하지 않도록 하는 것이다.

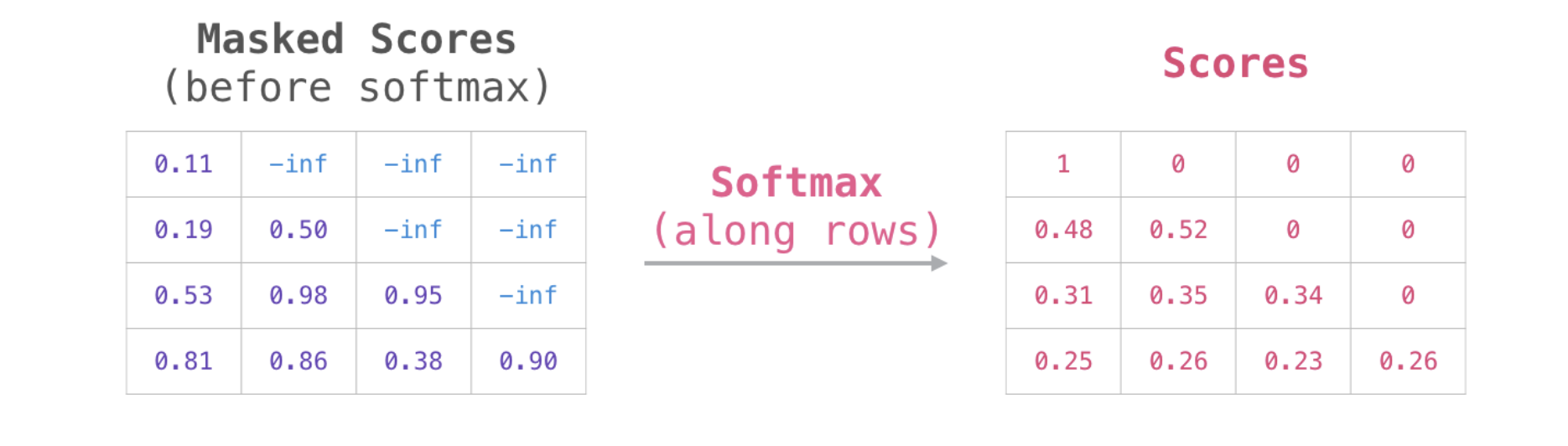
[출처] : https://jalammar.github.io/illustrated-gpt2/

주의 할 점은 반드시 masking은 softmax 함수를 적용하기 전에 이루어져야 한다는 것이다. 간단히 masking을 하는 방식을 살펴보면 먼저 하삼각행렬로 mask를 만든다음 mask의 값 중 0인 부분의 인덱스에는 음의 무한대(실제로 컴퓨터에서는 표현할 수 없으므로 음의 매우 작은 소수 값을 취한다)으로 그렇지 않은 부분은 원래의 attention score 값을 유지한다.

Decoder를 코드로 구현하면 다음과 같다.

class DecoderLayer(nn.Module):
    def __init__(self, hidden_dim, n_heads, pf_dim, dropout_ratio, device):
        super().__init__()

        self.self_attn_layer_norm = nn.LayerNorm(hidden_dim)
        self.enc_attn_layer_norm = nn.LayerNorm(hidden_dim)
        self.ff_layer_norm = nn.LayerNorm(hidden_dim)
        self.self_attention = MultiHeadAttentionLayer(hidden_dim, n_heads, dropout_ratio, device)
        self.encoder_attention = MultiHeadAttentionLayer(hidden_dim, n_heads, dropout_ratio, device)
        self.positionwise_feedforward = PositionwiseFeedforwardLayer(hidden_dim, pf_dim, dropout_ratio)
        self.dropout = nn.Dropout(dropout_ratio)

    # 인코더의 출력 값(enc_src)을 어텐션(attention)하는 구조
    def forward(self, trg, enc_src, trg_mask, src_mask):

        # trg: [batch_size, trg_len, hidden_dim]
        # enc_src: [batch_size, src_len, hidden_dim]
        # trg_mask: [batch_size, trg_len]
        # src_mask: [batch_size, src_len]

        # self attention
        # 자기 자신에 대하여 어텐션(attention)
        _trg, _ = self.self_attention(trg, trg, trg, trg_mask)

        # dropout, residual connection and layer norm
        trg = self.self_attn_layer_norm(trg + self.dropout(_trg))

        # trg: [batch_size, trg_len, hidden_dim]

        # encoder attention
        # 디코더의 쿼리(Query)를 이용해 인코더를 어텐션(attention)
        _trg, attention = self.encoder_attention(trg, enc_src, enc_src, src_mask)

        # dropout, residual connection and layer norm
        trg = self.enc_attn_layer_norm(trg + self.dropout(_trg))

        # trg: [batch_size, trg_len, hidden_dim]

        # positionwise feedforward
        _trg = self.positionwise_feedforward(trg)

        # dropout, residual and layer norm
        trg = self.ff_layer_norm(trg + self.dropout(_trg))

        # trg: [batch_size, trg_len, hidden_dim]
        # attention: [batch_size, n_heads, trg_len, src_len]

        return trg, attention

[소스 코드 출처] : https://colab.research.google.com/drive/1mt5G4MMneREGuQbaYYIfL_C1cvTTKIK1#scrollTo=0jn4VCWdXhK5

class MaskedSelfAttention(nn.Module):
    def __init__(self, config):
        super().__init__()
        assert config.hidden_size % config.num_attention_heads == 0
        self.use_cache = config.use_cache # TRUE

        self.hidden_size = config.hidden_size # 768
        self.num_attention_heads = config.num_attention_heads # 12
        self.head_dim = self.hidden_size // config.num_attention_heads # 64

        self.attn = Conv1D(3 * self.hidden_size, self.hidden_size)
        self.proj = Conv1D(self.hidden_size, self.hidden_size)

        self.attenton_dropout = nn.Dropout(config.attn_pdrop)
        self.residual_dropout = nn.Dropout(config.resid_pdrop)

    def forward(self, hidden_states, attention_mask=None):        
        Q, K, V = self.attn(hidden_states).split(self.hidden_size, dim=2)

        batch_size = hidden_states.shape[0] 
        # [batch_size, n_heads, seq_len, head_dim]
        Q = Q.view(batch_size, -1, self.num_attention_heads, self.head_dim).permute(0, 2, 1, 3) 
        K = K.view(batch_size, -1, self.num_attention_heads, self.head_dim).permute(0, 2, 1, 3)
        V = V.view(batch_size, -1, self.num_attention_heads, self.head_dim).permute(0, 2, 1, 3)

        if self.use_cache is True:
            present = (K, V) # 현재 상태 저장
        else:
            present = None
            
        ### Masking 적용 ###

        # QK^T / sqrt(d_k) 계산 
        attention_score = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.head_dim)

        # mask 만들기 
        Max_seq_len =  hidden_states.size(-2)
        # mask shape :  [1,1,max_seq,max_seq]
        mask = torch.tril(torch.ones((Max_seq_len, Max_seq_len), dtype=torch.uint8)).view(1,1,Max_seq_len,Max_seq_len)

        # attention_score에서 mask 값이 0인 부분의 위치는 음수의 아주 작은 값(-1e4)으로 채운다 
        attention_score = torch.where(mask, attention_score,torch.tensor(-1e4))

        # softmax 적용
        attention_score = F.softmax(attention_score, dim=-1)

        # 최종 Scaled Dot-Product Attention
        # 1. softmax 적용 결과에 dropout을 수행.
        attention_score = self.attenton_dropout(attention_score)

        # 2. softmax  * V 수행(행렬 곱셈) - Matrix Multiplication 
        outputs = torch.matmul(attention_score, V)

        # outputs size[batch size, max_sequence,hid_dim]에 맞게 변경 
        outputs = outputs.transpose(1,2).contiguous().view(batch_size, -1, self.hidden_size)

        outputs = self.proj(outputs)
        
        outputs = self.residual_dropout(outputs)
        
        outputs = (outputs, present)

        return outputs

Positional Encoding

마지막으로 Positional Encoding을 설명하면서 마무리하고자 한다. 위에서 언급한 것과 같이 Transformer는 오로지 attention 으로만 기반이 되어있기 때문에 각 단어의 위치에 대한 정보가 없다. 따라서 이러한 위치 정보를 포함시키고자 position table을 만들게 되는데 다음 자료를 보면서 설명하겠습니다.

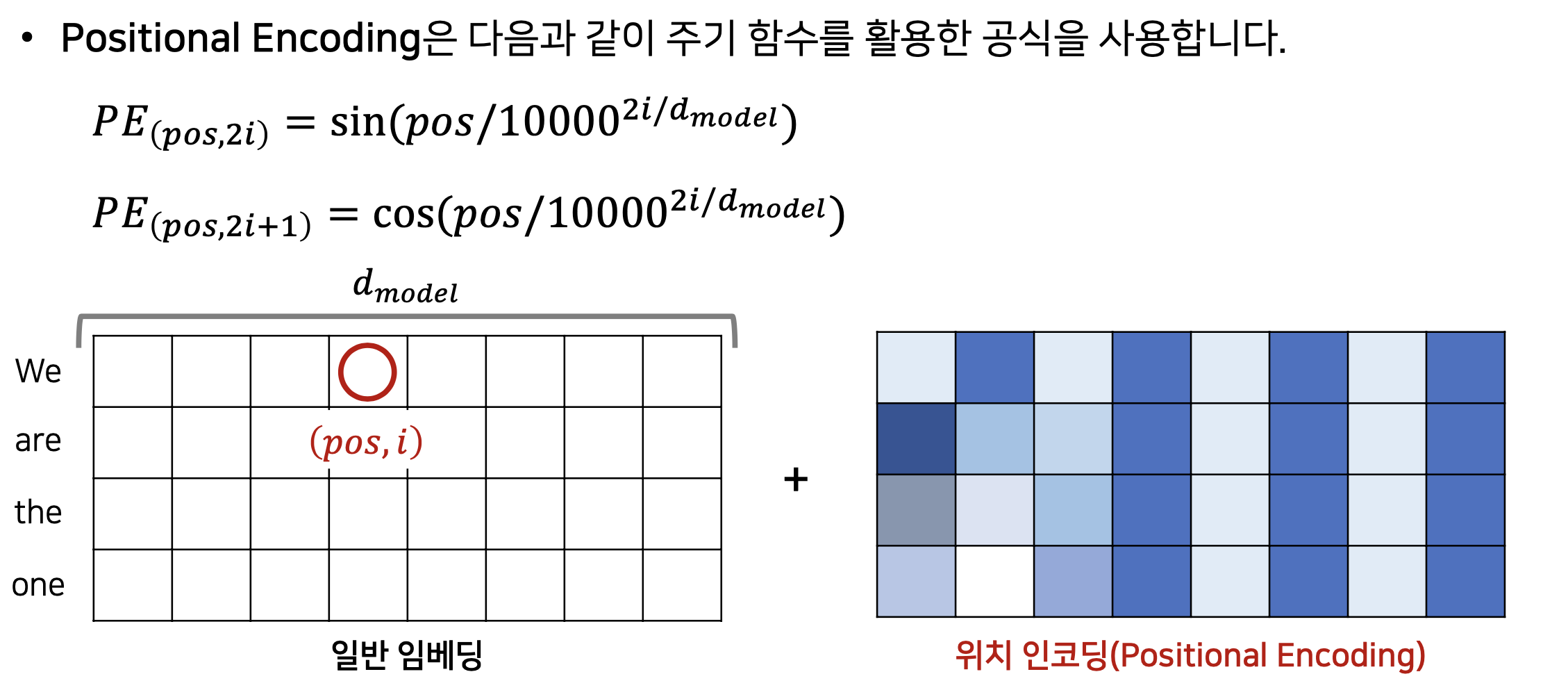
[출처]: https://github.com/ndb796/Deep-Learning-Paper-Review-and-Practice/blob/master/lecture_notes/Transformer.pdf

위 그림을 보면 pos는 token의 위치이고 i는 각 token의 차원을 의미한다. 따라서 위의 sin, cons 함수 공식을 대입해서 오른쪽의 table와 같은 위치 인코딩(정확히 input과 차원이 같은 행렬이다)을 만들어 낼 수 있고 이를 더하여 위치 정보를 담게 된다. Transformer이후에는 sin,cos와 같은 고정적인 함수를 사용하는 것이 아닌 Positional Encoding 자체를 하나의 학습의 대상으로 삼아서 Embedding layer를 사용하여 처리하고 있습니다.