저번 포스트의 Stack 과 Queue 에 이어집니다.

1. Linked List

Linked List 혹은 연결 리스트라 불리는 이것은 무엇이 “연결"되어 있다는 것일까요?

이 Linked List 는 Array 처럼 하나의 배열에 요소들이 순차적으로 정렬되어 있는 구조가 아닙니다. 대신 각 요소가 node 라는 데이터와 포인터로 이루어져 있습니다. 데이터는 말 그래도 데이터이며, 포인터는 다음 노드가 어디에 위치하는지 알려주는(포인트해주는) 표지판 같은 역할을 합니다. 그림으로 표현하자면 이런 식이 됩니다.

첫번째 노드는 1이란 데이터, 그리고 두번째 노드로 향하는 포인터를 가지고 있습니다.

이 포인터는 다음 노드를 가리키고 있으며 마지막 노드는 null 를 향합니다.
Linked List 의 장점은 요소의 추가/삭제가 용이하다는 점입니다. 포인터가 향하는 곳을 수정해주면 되는데 자세한 설명은 Method들을 설명하며 다시 하겠습니다.

그렇다면 단점은 무엇일까요? 바로 포인터가 단점이 되기도 합니다. Index 로 쉽게 데이터에 접근할 수 있는 Array 와 달리 Linked List 는 원하는 데이터를 찾기 위해 첫번째부터 포인터를 따라가야 발견할 수 있습니다.

1-1. Linked List 의 Property

Head

그림엔 표현되어 있지 않지만 첫번째 노드임을 판별하기 위해 head 란 노드가 첫번째 노드를 향하고 있습니다.

1-2.Linked List 의 Method

Non-Linear Structure

이제부터 나오는 구조들은 비선형 구조(Non-linear Structure)를 가집니다. Stack, Queue, 그리고 Linked List가 일방향의 흐름을 보여줬다면 다음의 자료구조들은 여러 갈래로 나눠 뻗어 나가며 조금 더 복잡한 구조를 띄게 됩니다.

2. Graph

좀 전 Linked List는 노드의 포인터는 한 개의 또 다른 노드를 향했습니다. 만약 포인터가 여러 노드를 가리킨다면 어떨까요?

예를 들어 1번 부터 4까지 가려면 경로가
[1] -> [2] -> [3] -> [4]
[1] -> [3] -> [4]
이런 식으로 나옵니다.

2-1. Graph 의 Property

• Vertex: Graph 에서는 노드라 불렀었던 저 1번을 “Vertex”(꼭지점)이라고 부릅니다.
• Edge: 포인터였던 화살표는 “Edge”(모서리)라 불립니다.
• In-degree: 자신에게 (들어)오는 Edge 들의 개수입니다.
• Out-degree: 반대로 자신이 향하는 Edge 들의 개수입니다.
  (위의 그림처럼 화살표가 아닌 서로 연결된 Graph를 Undirected Graph라 하는데 이 때 총 degree 를 셉니다.)

2-2. Graph 의 Method

각 vertex 와 edge를 관리하는 메서드들입니다.

• addVertex() - vertex를 추가합니다.
• removeVertex() - vertex를 제거합니다.
• addEdge() - Vertex들 사이에 Edge를 추가합니다.
• addEdge() - Vertex들 사이에 Edge를 제거합니다.

Graph를 구현하는 방식은 크게 2가지로,

• 첫번째는 2차원 배열을 이용하는 방식입니다. 이 때는 vertex 간 서로 연결을 확인하기 쉽지만, 2차원 배열을 사용하므로 공간이 차지하는 메모리가 큽니다.
• 두번째는 Linked List를 이용하는 방식이다. 이 방식은 연결 여부를 확인하는 게 오래걸리지만, 연결되어 있는 vertex 만큼만의 메모리를 이용하기에 효율적이다.

3. Tree

이번 구조 또한 비선형 구조입니다. 어떠한 이유로 Tree 라 불리는 것일까요?
바로 나무처럼 뿌리에서 가지를 쳐서 뻗어나가는 구조이기 때문입니다.
우리에게 가장 익숙한 것을 예시로 가져왔습니다.

출처: https://monsieursongsong.tistory.com/6

3-1. Tree Property

• Root node - A가 뿌리를 내리는 첫번째 노드가 됩니다.
• Child node - A가 뿌리를 내리면서 B-I 는 모두 누군가의 Child node가 됩니다.
• Parent node - A처럼 뿌리를 내리는 B-D는 모두 누군가의 Parent node가 됩니다.
• Sub-tree - B-D처럼 뿌리를 내린 부분은 조그만 sub-tree라고 할 수도 있습니다.
• Leaf node - H, I처럼 마지막 level에 존재하는 node가 leaf node가 됩니다. 나무의 끝에 있는 것이 나뭇잎인걸 생각하면 이해에 도움이 됩니다.

4. Binary Search Tree

Binary Search Tree 는 갈래가 항상 두 갈래로 생기게 됩니다.
왼쪽/오른쪽을 나누는 기준은 Child node 의 값이 Parent node의 값보다 작으면 왼쪽, 크면 오른쪽에 위치하게 됩니다.

4-1. Binary Search Tree 의 Property

각 노드는 데이터와 left 와 right 으로 향하는 포인터를 가지고 있습니다. 이 노드의 데이터 값보다 작은 노드를 추가하려면 left 를 연결, 크다면 right를 연결해줍니다.

4-2. Binary Search Tree 의 Methods

• addChildNodeLeft() : 추가하려는 Child node 의 값이가 Parent Node값보다 작을 때 Parent node의 왼쪽에 추가한다.
• addChildNodeRight() : 추가하려는 Child node 의 값이가 Parent Node값보다 클 때 Parent node의 오른쪽에 추가한다.

5. Hash Table

Hash Table 은 주어지는 key 값을 통해 value를 저장, 후에 검색할 수 있는 구조이다. 먼저 주어진 key 와 value 는 hash function 을 통해 hashing 이 이루어진다. 이렇게 hashing 이 된 hash value는 bucket 안에 저장이 된다. 그렇게 되면 간단히 key를 통해서 value를 검색하는 것이 가능해진다.

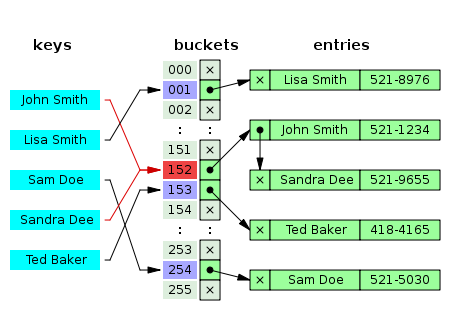
출처: https://en.wikipedia.org/wiki/Hash_table

그런데 만약 위의 그림처럼 저장된 index가 같을 경우, Linked-List 를 이용하여 충돌한 두 hash value를 연결시켜 관리한다.

5-1. Hast Table Property

• Hash function: key-value를 정렬/저장하기 위해 특정한 인덱스를 리턴하는 함수.
• Bucket: hasing된 value가 저장되는 곳.
• key: 요소의 key값, hash value를 검색할 때 사용할 수 있다.
• value: key값을 이용해 Bucket 안에 저장된 value를 탐색할 수 있다.

5-2. Hast Table 의 Methods

• Hash function: Hash Table 의 장점은 Hasing 이 되어 저장된 value 에 접근(검색, 삽입, 삭제)하기 용이하다는 것이다. 그리고 Hasing 이 될 때 충돌이 일어나지 않는다면 더욱 좋을 것이다. 그렇기에 좋은 Hash function을 만드는 것이 정말 중요하다. 그럼에도 충돌을 완전히 피할 수는 없지만, 충돌을 피하기 위한 여러 수학적 방법들이 고안되어 있다. 지금 생각할 수 있는 예시는 1과 자기자신을 공약수로 가지는 소수를 이용하여 최대한 겹치는 수를 배제하는 방식이 있다.

참고

https://boycoding.tistory.com/33
https://www.zerocho.com/category/Algorithm/post/584b9033580277001862f16c
https://monsieursongsong.tistory.com/6