좋은 알고리즘이란 무엇일까? 사람에 따라 다르지만 적어도 명확히 나눌 수 있는 기준들이 몇가지 있다. 이 중 중요한 두가지가 있는데 바로 Time Complexity 와 Space Complexity 이다. 최대한 한 문장으로 나름 정리해보았다.
- Time Complexity - 코드가 실행될 때, 알고리즘의 연산으로 인해 걸리는 시간에 따라 나눠진 복잡도.
- Space Complexity - 코드가 실행될 때, 알고리즘의 연산으로 인해 사용되는 공간(데이터)에 따라 나눠진 복잡도.
오늘 다룰 내용은 Time Complexity 와 이것의 표기법 Big-O Notation 이다.
Time Complexity
먼저 간단한 예시로, 아래와 같은 배열이 주어졌을 때, 만약 한 배열의 요소들 중 가장 큰 차이를 알아내는 것은 얼마나 걸릴까?
let arr = [2, 3, 4, 5, 6, 7, 8] //length is defined.
첫번째로는 좀 오래 걸리는 방법이다: 모든 요소를 하나하나 비교하는 법이다.
2와 3, 2와 4, 2와 5,… 그 다음은 3과 4, 3과 5,… 와 같이 각각 비교한다.

이 표를 보면 총 경우의 수는 7 7 = 49 가지이다.
이 수는 배열의 n개의 요소에 따라 달라지므로 Time Complexity는 ```n n = n²```가 된다.
n² 은 n 이 커질수록 기하급수적으로 늘어나므로 분명 더 나은 방법이 존재할 것이다.
만약 최소값과 최대값을 찾고 그 둘을 비교하는 것은 어떨까?

이 때는 최소값을 찾기 위한 7번 + 최대값을 찾기위한 7번 = 14번.
즉, n + n = 2n 이 되었다. 좀 전의 n² 보다 훨씬 나은 방법이 되었다.
그렇다면 만약 이 배열이 sort된 배열이란 것을 알고 있다면 더 효율적일 수 있을 것이다.
배열의 마지막 값과 첫번째 값을 바로 가져와서 빼면 8 - 2 = 6란 것을 알 수 있다.
이 경우는 1+1=2 가 되며, 우리는 2n 보다도 더 빠른 방법을 발견하였다.
Big-O notation
우리가 방금 3가지 방법을 계산한 것과 비슷하게 표시한 표기법 을 Big-O notation 이라고 부른다.
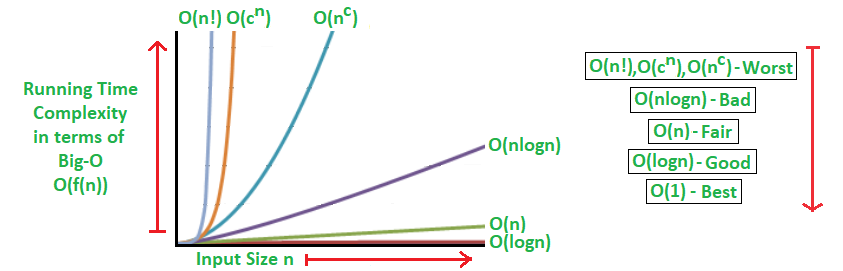
출처: https://www.geeksforgeeks.org/analysis-algorithms-big-o-analysis/
x축은 input의 크기, y축은 running time 이다. input이 커질 수록 running time이 증가하는 건 자연스러운 현상이지만 위의 그래프를 보면 차이가 확연히 드러난다.
Big-O notation을 표기할 때 주의해야할 점은 상수(constant)는 빼고 표기한다는 점이다. 예를 들어 좀 전의 2n 같은 경우도 그냥 n으로 표기한다. 그 이유는 상수가 미치는 영향은 지수(exponential)의 영향에 비해 미미하기 때문이다.
이렇게 알고리즘을 짤 때 나의 코드가 컴퓨터의 실행에 미치는 시간적인 혹은 공간(데이터)적인 영향을 고려하며 작성한다면 조금 더 효율적이고 만족스러운 프로그램을 만들 수 있게 될 것이다.
