변성 (Variant)

종종 객체 지향 언어에서 공변성과 반공변성이란 단어가 나옵니다. 대개 서브타입 관계를 논할 때 등장하는데, 저는 주로 클래스의 메서드 오버라이딩과 타입스크립트의 타입 응용에서 경험했습니다.

공변성과 반공변성은 뭘까요? Microsoft .NET 설명서는 "원래 지정된 것보다 더 많이 파생되거나(더 구체적인) 더 적게 파생된 형식(덜 구체적인)을 사용할 수 있는 능력을 지칭하는 용어" 라고 말합니다. 타입의 확장을 고민해야 할 개발자에게 가장 현실적인 표현이죠.

그러나 변성에는 공변성과 반공변성만이 전부가 아닙니다. 무공변성(불변성)과 이변성 또한 존재합니다. 대부분의 경우에서 이 개념들은 베타적 개념이므로, 실제 개발에서 중요하게 여길 필요는 없습니다. 여러 케이스에서 독특한 부분들을 담당하고 있지만 지엽적으로 이해해도 무방하기 때문입니다.
그럼에도 불구하고 이 글에선 네 가지 변성을 모두 설명하는 것을 목표로 두겠습니다.

정의

변성에는 총 네가지 유형의 변성이 있습니다. 크게 공변성과 반공변성으로 나뉘고, 이들을 동시에 충족하거나 그렇지 않은 게 있습니다.

정의가 불확실할 수 있습니다.
개인적으로 변성들에 대한 완벽한 정의 출처를 찾지 못했습니다. 만약 알고 계신다면 부디 댓글로 알려주세요.
이 글에선 위키피디아에 기재된 정의를 서브타입 관계로 설명하겠습니다.

• 공변성, T ≤ S라면 F<T> ≤ F<S> 이다.
• 반공변성, T ≤ S라면 F<S> ≤ F<T> 이다. 즉 공변의 반대다.
• 이변성, 공변하면서 반공변하다.
• 변성, 공변하거나 반공변하거나 이변하면 변성이다.
• 불변성(또는 무공변성), 공변하지도 반공변하지도 않다.

참고: T ≤ S라 함은 T가 S의 서브타입(또는 T가 S)이란 뜻입니다. 동의어로 부분집합, 파생된 타입, S에 할당할 수 있는 타입 등이 있습니다. 클래스에서 T extends S를 생각해보세요.

변성은 서브타입 관계와 서브타입 관계의 관계에 대한 성질을 일컫습니다.
공변성을 예로 들어 보면, T가 S의 서브타입이면서 F<T>가 F<S>의 서브타입이면 이 서브타입 관계의 관계를 보고 공변하다고 말합니다. 반공변성은 이 관계의 반대에 해당하며, 이변성은 이 관계 또는 반대의 관계(반공변성)에 해당합니다. 불변성은 이 관계도, 그 반대의 관계도 아닙니다. 즉, 애초에 아무런 관계가 없다고 정의합니다.

응용

앞서 말씀드렸다시피 저는 메서드 오버라이딩과 타입스크립트의 타입 응용에서 공변과 반공변을 경험했습니다. 실제 사례를 통해 공변과 반공변과 같은 변성들이 어떻게 개발에 영향을 끼치는지 이해해 봅시다.

메서드 오버라이딩

OOP에서 가장 유명한 원칙 중 하나인 SOLID 원칙을 아시나요? 그 중 하나인 리스코프 치환 원칙에선 메서드 오버라이딩에 대해 리턴 타입의 공변성, 매개변수 타입의 반공변성을 강제하고 있습니다. 앞선 설명에 따르면 오버라이딩할 메서드의 리턴 타입은 기존 타입 또는 그 서브타입들로 좁혀야 하고, 반대로 파라미터 타입은 기존 타입 또는 그 슈퍼타입들로 넓혀야 합니다.

근본적으로 왜 이래야 할까요? 왜 메서드를 오버라이딩할 때 그 메서드의 슈퍼타입에 의존해야 하죠?
아래 TypeScript 예제 코드를 봅시다.

class Parent {
	// TypeScript에선 lambda의 파라미터 타입만이 반공변성을 지닙니다.
	public method = (param: string | number) => {

	}
}

class Child1 extends Parent {
	public override method = (param: string | number | symbol) => {

	}
}
class Child2 extends Parent {
	// 파라미터 타입은 반공변적이여야 하므로 param의 타입은 Parent#method의 param의 슈퍼타입이여야 합니다.
	public override method = (param: string) => {

	}
}

먼저 리스코프 치환 원칙에 대입하여 코드의 문제를 설명해 봅시다.
Parent는 method가 string 또는 number 타입의 인자를 받아 뭔갈 하기로 계약했음에도 불구하고 Child2는 method가 string 타입의 인자만 받기로 역할을 수정했습니다. 리스코프 치환 원칙은 서브타입S의 객체가 그것의 슈퍼타입T의 객체로 치환될 수 있단 원칙인데, (param: string) => void 함수는 (param: string | number) => void 함수에 할당할 수 없어서 Child2 객체가 Parent에 할당할 수 없게 됩니다. 즉, 원칙을 위반했습니다.

그러나 원칙을 어긴 건 크게 와닿지 않습니다. 원칙을 어긴 게 근본적으로 무슨 문제죠?
이 문제를 그냥 무시한다면 어떻게 될지 생각해 봅시다.

class Parent {
	public method = (param: string | number) => {
		console.log(String(param).slice(0));
	}
}

class Child extends Parent {
	public override method = (param: string) => {
		// param은 무조건 string이니 아무런 문제가 없어야겠죠?
		console.log(param.slice(0));
	}
}

function doSmhWithParent(parent: Parent) {
	parent.method(12);
}

doSmhWithParent(new Child());

위 코드는 Parent 타입으로 뭔갈 할 doSmhWithParent 함수가 Parent#method는 number를 인자로 넘겨도 된다고 생각하여 12를 인자로 넘긴 코드입니다.
그러나 정작 그 함수에 인자로 넘긴 객체는 원칙을 어긴 Child의 객체였고, 심지어 number를 인자로 넘겨선 안 되도록 함수를 고쳐놓은 상태입니다.

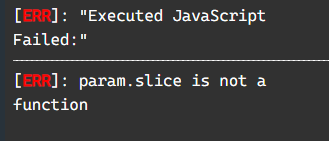
이것이 매개변수가 서브타입이 아니라 슈퍼타입이어야 하는 이유입니다. Parent의 모든 자식 클래스의 객체들은 Parent에 할당할 수 있으므로 method 함수의 인자 타입은 최소 string | number 이여야 합니다.

주의: 항상 그렇진 않습니다.
여러 언어들은 자체적으로 매개변수 타입의 공변성과 반공변성을 선택적으로 주거나 동시에 주는 등의 차별을 두고 있습니다. 종종 매개변수의 서브타입 관계가 클래스의 서브타입 관계와 일치하는 게 더 직관적인 경우가 있기 때문입니다. 이런 예외적인 경우에 대해서 C#, kotlin, java 같은 언어들은 제너릭을 통해 공변과 반공변을 명시케 하고 있습니다.

공변/반공변	Java	Kotlin/C#	TypeScript
공변성	T extends Parent	out Parent	T extends Parent
반공변성	T super Parent	in Parent	arrow function으로 선언

이에 대해선 함수 줄여 쓰기에서의 이변 문단에서 추가로 이야기하겠습니다.

그럼, 반환 타입은 왜 매개변수 타입과 달리 공변적이여야 할까요? 반환값을 사용할 경우를 생각해 보면 좀 더 손쉽게 이해할 수 있습니다. Parent#method가 {foo:string} 타입만 반환하도록 정한 상태에서 Child#method가 object 타입만 반환하도록 멋대로 바꾸면 위 에러와 같은 외통수가 똑같이 터지겠죠.

Union to Intersection

앞서 설명한 메서드의 공변성과 반공변성을 타입스크립트의 타입에선 좀 더 유연하게 응용할 수 있습니다. 이해를 위해 겸사겸사 이 글을 처음 쓸 때 다뤘던 U2I(Union to Intersection)를 예로 들어보겠습니다.

type UnionToIntersection<U> = 
  (U extends unknown ? (k: U) => void : never) extends (k: infer I) => void 
    ? I 
    : never;

UnionToIntersection는 타입 분배와 반공변적인 매개변수 타입의 추론을 이용하여 U의 가능한 모든 슈퍼 타입 I를 추론하는 타입입니다. 예를 들어 { foo: "bar" } | { bar: "foo" }타입을 인자로 받아 { foo: "bar" } & { bar: "foo" } 타입을 내뱉습니다. 저 타입에선 타입 U에 할당 가능한 타입 I를 추론하는데, 매개변수 타입은 반공변적이므로 I는 U의 슈퍼타입입니다. 그런데 어떻게 알지도 모르는 슈퍼타입을 추론할 수 있을까요? 어떻게 반공변성의 성질로 합집합을 교집합으로 바꿀 수 있죠?

답은 타입스크립트가 조건부 타입을 추론하는 알고리즘에 있습니다.
조건부 타입이 처음 나온 typescript 2.8v 릴리즈 노트에는 조건부 타입을 해석하거나 연기하는 내용에 관해 설명합니다.

Next, for each type variable introduced by an infer (more later) declaration within U collect a set of candidate types by inferring from T to U (using the same inference algorithm as type inference for generic functions). For a given infer type variable V, if any candidates were inferred from co-variant positions, the type inferred for V is a union of those candidates. Otherwise, if any candidates were inferred from contra-variant positions, the type inferred for V is an intersection of those candidates. Otherwise, the type inferred for V is never.
다음으로, U 내에서 infer(나중에 자세히 설명) 선언에 의해 도입된 각 타입 변수에 대해 (일반 함수에 대한 타입 추론과 동일한 추론 알고리즘을 사용하여) T에서 U로 추론하여 후보 타입 집합을 수집합니다. 주어진 타입 변수 V에 대해 공변적인 위치에서 유추된 후보가 있는 경우, V에 대해 유추된 타입은 해당 후보들의 유니온 타입이 됩니다. 그렇지 않고, 반공변적인 위치에서 유추된 후보가 있는 경우, V에 대해 유추된 타입은 해당 후보들의 인터섹션 타입이 됩니다. 그렇지 않으면, V에 대해 추론된 타입은 never입니다.

이 내용은 조건부 타입이 T extends infer V ? X : Y 처럼 infer 선언이 섞여있을 때, infer로 선언한 타입 변수를 어떻게 추론하는지에 대한 내용입니다. 우리가 가장 주목해야 할 부분이죠.

이 내용은 문서에서 후술한 Type inference in conditional types 문단의 예제 코드들을 통해 이 문서가 무엇을 말하는 것인지를 이해할 수 있습니다. 아래 코드는 그 예제 코드들을 살짝 수정한 임의의 코드입니다. typescript playground에서 확인해 보세요.

type A<T> = T extends { a: () => infer U; b: () => infer U }
  ? U
  : never;
type a = A<{ a: () => string; b: () => number }>;

type B<T> = T extends { a: (x: infer U) => void; b: (x: infer U) => void }
  ? U
  : never; // string | number
type b = B<{ a: (x: [string]) => void; b: (x: [number]) => void }>; // [string] & [number]

A는 "공변적인 위치"에서, B는 "반공변적인 위치"에서 "후보 타입들"을 추론합니다. 이 후보 타입들이란 조건부 타입에서 조건을 성립시킬 수 있는 타입의 후보들이란 뜻입니다. 문서에 따라, 공변적인 위치인 A는 후보들을 유니온 타입(합집합)으로 묶었고 반공변적인 위치인 B는 인터섹션 타입(교집합)으로 묶었습니다. (타입 b에서 string과 number를 배열로 감싼 이유는, 원시형 타입들은 서로소 타입이기 때문에 string & number같은 원시형 타입들의 교집합은 있을 수 없으므로 공집합(never)이 나오기 때문입니다.)

즉, 이 문단의 처음에서 { foo: "bar" } | { bar: "foo" }의 슈퍼타입이 어떻게 나왔냐 하면 I 타입 변수가 공변적인 위치에서 { foo: "bar" }와 { bar: "foo" }로 후보가 추론되었고, infer로 선언된 타입 변수의 문법적 성질에 의해 인터섹션 타입으로 추론되었다고 말할 수 있습니다.

그러나 아직 의문이 남아 있습니다. 도대체 어떻게 { foo: "bar" } | { bar: "foo" }의 슈퍼타입으로 { foo: "bar" }와 { bar: "foo" }가 추론된 거죠? 상식적으로 { foo: "bar" } | { bar: "foo" }의 슈퍼타입은 자기 자신 또는 자신을 포함한 제 3의 타입이어야 합니다. { bar: "foo" }는 오히려 서브타입이잖아요!

이 의문의 해답은 분배 조건부 타입(Distributive conditional types)에 있습니다. (대개 타입을 분배한다고 말합니다.)

Conditional types in which the checked type is a naked type parameter are called distributive conditional types. Distributive conditional types are automatically distributed over union types during instantiation. For example, an instantiation of T extends U ? X : Y with the type argument A | B | C for T is resolved as (A extends U ? X : Y) | (B extends U ? X : Y) | (C extends U ? X : Y).
검사된 타입이 네이키드 타입 매개변수인 조건부 타입을 분배 조건부 타입이라고 합니다. 분배 조건부 타입은 인스턴스화 중에 유니온 타입에 자동으로 분배됩니다. 예를 들어, 타입 파라미터 T에 A | B | C가 있다면 T extends U ? X : Y의 인스턴스화는 (A extends U ? X : Y) | (B extends U ? X : Y) | (C extends U ? X : Y)로 해석됩니다.

정보: 네이키드 타입(naked type)이란 배열, 튜플, 함수, 또는 제너릭 타입과 같은 타입들로 래핑되지 않은 타입을 말합니다. ("naked"자체가 "벌거벗은"이란 뜻) - StackOverFlow 참조

이 이해를 기반으로 앞서 선언한 UnionToIntersection를 봅시다.

type UnionToIntersection<U> = 
  (U extends unknown ? (k: U) => void : never) extends (k: infer I) => void 
    ? I 
    : never;

그리고 이 타입을 사용한 타입 a도 봅시다.

type a = UnionToIntersection<{ foo: string } | { numbericBar: number }>

이 타입 a는 타입 분배에 의해 내부적으로 아래와 같은 꼴이 된 것입니다.

type a1 =
  ((k: { foo: string }) => void) | 
  ((k: { numbericBar: number }) => void) 
    extends (k: infer I) => void ? I : never;

그리고 놀랍게도 그 결과는 똑같습니다. - typescript playground에서 직접 확인해 보세요.

즉, { foo: "bar" } | { bar: "foo" }에서 { foo: "bar" }의 슈퍼타입 따로, { bar: "foo" }의 슈퍼타입 따로 추론하는 것입니다. 그리고 그것들의 슈퍼타입은 달리 알 바가 없으니 자기 자신이 추론됩니다. 그렇게 추론의 후보 타입들로 유니온 타입을 구성하는 타입들이 나오는 것입니다. 그리고 infer의 문법적 특성에 의해 이렇게 나온 후보 타입들이 인터섹션 타입으로 묶여서 타입 I로 추론되는 것이고요. 그리고 최종적으로 이렇게 추론된 타입 I가 조건부 타입에 의해 결과로 나오는 것입니다.

UnionToIntersection은 매우 흥미롭고 대표적인 타입스크립트 조건부 타입의 예입니다. 변성을 이해하는 겸사겸사 이 U2I에 대해서도 분석했는데, 꽤 재미있어서 분량 조절을 실패해버렸네요 ;P

함수 줄여 쓰기에서의 이변

이변성에 대해선 그 모습을 흔히 보기가 힘듭니다. 공변성 또는 반공변성을 만족시키는, 즉 자신을 포함한 모든 슈퍼타입과 모든 서브타입을 관계에 포함하는 성질이기 때문입니다. 그러나 타입스크립트에는 유명한 케이스가 하나 존재합니다.

바로 함수 줄여 쓰기 선언입니다. strictFunctionTypes TS컴파일러 옵션을 다루는 현섭 님의 아티클의 이변성 문단에선 줄여 쓰기 방식에서 매개변수 타입이 이변적이라고 설명합니다.

정리하자면, 줄여 쓰기(shorthand) 방식(set(item: T): void;)은 메서드 파라미터를 이변적으로 동작시키기 위한 표기법이고, 프로퍼티 방식(set: (item: T) => void;)은 메서드 파라미터를 반공변적으로 동작시키기 위한 표기법이라고 볼 수 있겠습니다.

정리하자면 Array<string | number>의 push 메서드의 타입은 (...item: Array<string | number>) => void이지만, 서브타입인 Array<number>의 push 메서드의 타입은(...item: Array<number>) => void이므로 타입 에러가 발생하는 문제가 생깁니다. 정작 number를 넣어도 문제가 전혀 없으니 현실적인 문제도 없고, 결국 유명무실한 문제가 발생한 것입니다.
따라서 이러한 현실과 원칙의 괴리를 해결하기 위해 이변성의 탈출구를 작위적으로 마련한 것입니다. C#같은 다른 언어는 이변성 대신 예약어로 해결했는데 말이죠... 🤔

참고로 이렇게 작위적으로 만든 탈출구는 strict하게 타입을 검사해도 유효해서, 타입 체계의 큰 취약점으로 작용할 수 있습니다. 그래서 eslint는 이를 경고하는 규칙을 가지고 있습니다.

끝

이 글에선 공변성과 반공변성, 이변성에 대해서 메서드 오버라이딩과 U2I, 타스의 특별한 이변성 구멍을 예로 들어 설명해 드렸습니다. 단순히 예에 그치지 않고 완벽한 이해를 위한 설명을 야무지게 채워 넣었습니다. 개인적으로 변성의 이해에 대해 확신이 들었고, 여지껏 갈팡질팡한 U2I도 완벽히 이해해서 속이 후련합니다.

추가로 불변성에 대해선 따로 이야길 안 했는데, 애초에 변성이 없으면 다 무공변성이기 때문입니다. 매서드 오버라이딩의 파라미터를 빼면 대부분이 공변과 무공변일테니 특별히 예를 드는 게 무의미하죠.

참고

• 제네릭의 공변성(Covariance) 및 반공변성(Contravariance)
• 리스코프 치환 원칙
• 공변성과 반공변성 (컴퓨터 과학), Covariance and contravariance (computer science)
• 공변성이란 무엇인가
• 공변성, 반공변성, 무공변성이란?
• typescript 2.8v 릴리즈 노트