서론
백준 문제 중 모든 브론즈5 문제를 풀고 딱 하나, 27434번 팩토리얼 3 문제가 남아있었다.
이전 문제였던 27433번 팩토리얼 2 문제와 비슷해서 아 이거 BigInt면 끝나겠네라고 간과하며 풀었으나 시간 초과로 퇴짜맞았다!

왜그런지 문제를 다시 읽어보니 10만 팩토리얼을 4초 안에 계산해야 하는 문제였던 것이다.
주변인들에게 물어봐도 어 팩토리얼? big integer면 되겠네 라는 답변만 들을 수 있었다.
왜냐하면 이 문제는 실제로 pypy3로 쉽게 풀 수 있기 때문이다.
 |  |
|---|---|
| 팩토리얼 함수를 쓰든 | 직접 for문으로 하든 |
상관없이 모두 시간초과 없이 정답 처리가 된다. 놀랍게도 pypy3은 정답 언어의 높은 비율을 차지하고 있다.
정답 799개 중
- 710개가 pypy3로 구성된 코드다. (88.8%)
- 10개가 cpp로 구성된 코드다. (1.2%)
- 29개가 java/kotlin로 구성된 코드다. (3.6%)
- 20개가 go로 구성된 코드다. (2.5%)
- 18개가 rust로 구성된 코드다. (2.2%, 그런데 2명이 여러번 제출했다)
- 6개가 ruby로 구성된 코드다. (0.7%)
- 1개가 swift 구성된 코드다. (0.1%)
- 1개가 node.js로 구성된 코드다. (0.1%)
이러한 기형적인 비율엔 이유가 있으니...

애당초 의도된 일이였던 것이다!
그래서 pypy3에 굴복하고 끝내도 되지만 node.js로 끝까지 밀어붙여놓고 포기하는건 너무 억울했다. 그래서 가장 최근의 자바 제출을 보니 PriorityQueue를 사용하고 있던 것이다. 언어 치트라니
PriorityQueue가 왜 빠른가
를 알기 전에 몇가지 정리가 필요하다.
- 개념 정리 - 아래의 벤치마킹에서 사용할 함수는 총 5개이므로 이를 설명하고 시간복잡도와 함께 설명할 예정이다.
- 벤치마킹 - 벤치마킹은 일종의 성능 테스트 실험이다. 그러므로 몇가지 변인을 설정해야 한다.
- 통제변인: 입출력
- 조작변인: 자료구조
개념 정리
팩토리얼 벤치마킹에서 사용할 방법은 총 다섯개로, 반복문, 배열, 반전된 배열, 최소 힙, 최대 힙이 있다. 순서대로 설명하기 전에 추가로 설명할 것이 있다.
BigInt: JS의 BigInt 폴리필 분석 - JSBI
BigInt는 일반적으로 number 자료형이 담을 수 있는 상한선을 넘겨버린 매우 큰 수다루기 위한 자료형이다. 자바스크립트에서 BigInt가 어떻게 동작하는지 알기 위하여 몇가지 조사와 분석을 해보았다.
그러기 위해서 JSBI를 접했다. JSBI는 JavaScript BigInteger의 Polyfill이다. JSBI의 설명을 보면 자신들이 만든 JSBI 클래스가 ES2020에 있는 BigInt 내용이라고 설명한다.
JSBI is a pure-JavaScript implementation of the ECMAScript BigInt proposal, which officially became a part of the JavaScript language in ES2020.
JSBI는 ES2020에서 공식적으로 자바스크립트 언어의 일부가 된 ECMAScript BigInt 제안을 순수 자바스크립트로 구현한 것입니다.
JSBI 클래스를 처음 보면 바로 알 수 있는 점은 배열이다! 추가적으로 조사해보면 정말 많은 곳에서 Big Integer를 자릿수 단위의 배열로 구현하는걸 적지않게 볼 수 있다.
 |
|---|
JSBI의 곱셈 구현 코드는 아래와 같은데 전문가의 도움으로 이것이 다항식의 곱 구현방식인 FFT와 카라추바 중 카라추바 알고리즘을 사용했단 사실을 알 수 있었다.
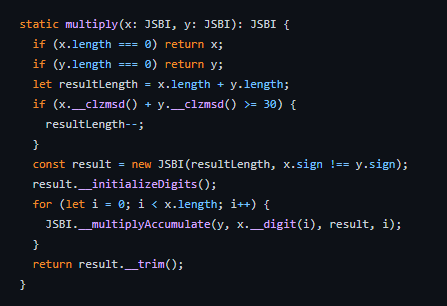 | 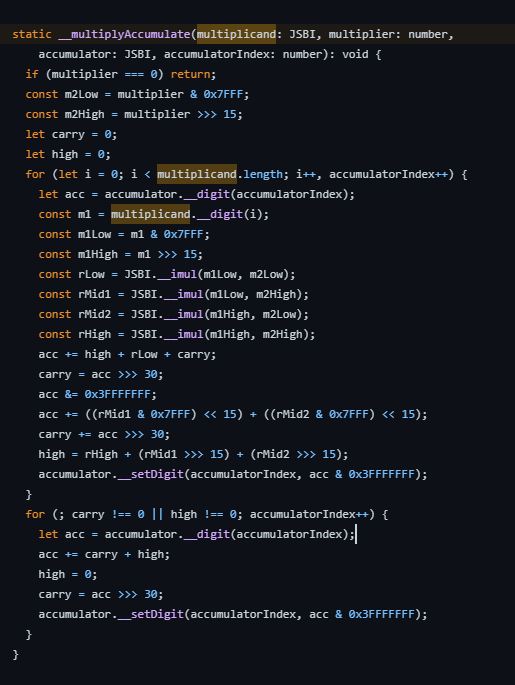 |
|---|
더 자세한 확답을 받기 위해 ChatGPT에게 물어보면 카라추바 알고리즘이나 톰-쿡 알고리즘을 사용한다고 말한다.

또한 톰 쿡 알고리즘 wikipidia와 카라슈바 알고리즘 wikipidia 위키피디아 문서와, medium - A fast BigInt.js in an evening, compiling C++ to JavaScript 블로그의 Test & benchmark 문단 끝자리에서 카라슈바와 톰-쿡 알고리즘이 언급되고 그 특성을 설명한다.
톰 쿡 알고리즘 wikipidia
이런 부가적인 연산 때문에 톰-쿡 알고리즘은 작은 정수의 곱셈에 적용하면 일반 곱셈법보다 느려지기에 이 알고리즘은 적당히 큰 정수에 사용되며, 정수 크기가 훨씬 더 커질 경우는 시간복잡도가 Θ(n log n log log n)인 쇤하게-슈트라센 알고리즘이 더 빠르게 된다.
카라슈바 알고리즘 wikipidia
충분히 큰 n에 대해, 카라추바 알고리즘은 고전적인 곱셈법보다 적은 횟수의 시프트 연산과 한 자리 곱셈을 행한다. 하지만 작은 n에 대하여는 추가적인 덧셈과 시프트 연산 때문에 고전적인 곱셈법보다 속도가 느려진다. 그 경계는 컴퓨터의 플랫폼에 따라 달라진다. 대략적으로 곱하는 수가 2320 ≈ 2×1096 이상일 때 카라추바 알고리즘이 더 빠르다.
medium - A fast BigInt.js in an evening, compiling C++ to JavaScript
The results is a 5771 line of generated JavaScript code, comprising Karatsuba’s and Toom-Cook’s algorithm for fast multiplications, usable freely for any (not) so serious scope.
그 결과 5771줄의 자바스크립트 코드가 생성되며, 이 코드에는 Karatsuba와 Toom-Cook의 빠른 곱셈을 위한 알고리즘이 포함되어 있으며, 그다지 심각하지 않은 범위에서 자유롭게 사용할 수 있습니다.
이를 통해 얻은 정보들이 시사하는 바는 아래와 같다.
- JavaScript의 BigInt는 자릿수 배열을 가지고 큰 수를 표현하도록 구현됐으며 큰 수의 곱셈에 카라슈바와 톰-쿡 알고리즘이 사용되었다.
- BigInt의 곱셈은 작은 수에 사용할수록 비효율적이다.
자릿수 배열을 통해 어떻게 큰 수를 표현했을까?
단순히 12를 [1, 2] 과 같이 자릿수 단위로 배열에 나눠담은 것이다. 이를 숫자로 되돌린다면 예전 초중학교에서 했듯이 1 * 10 + 2하는 과정이 필요하므로 숫자로 되돌리는 수식은 Σ(index * 10 ^ length-index-1) 일 것이다.
문제는 이렇게 숫자로 표현할 수 없어 배열을 통해 다항식처럼 표현한 상태에서 곱셈을 한다면 우리가 직접 다항식을 곱하듯이 해야 할텐데 이러면 이중 반복문, 즉 O(N^2)의 상태가 되어버린다.
이때 FFT 및 카라슈바 알고리즘은 이 다항식의 곱을 N^2에서 NlogN으로 절감시킨 혁신적인 알고리즘이다.
의문: 격차가 작은 수들끼리 곱하는건 성능에 유의미한 결과를 낳는가?
위 내용에 따르면 결국 수가 커질수록 증가폭이 커지는 점은 여전하다. 그게 크게 줄어들었을 뿐. 이게 추가적으로 일으키는 의문은 서로 다른 두 자릿수에서 BigO는 무얼 기준으로 계산되는가? 이다. BigO는 항상 최악의 경우를 상정해야 하므로 가장 길이가 큰 수를 기준으로 둘 것이다. 그렇다면 O(N)의 N은 max(logA, logB) 일 것이다. 이에 따르면 수가 클수록 시간이 더 오래걸리니 차라리 작은 수들끼리 따로 곱하면 효율이 높을 것이란 추측에 도달한다.
그리고 덧붙여 격차가 아니라 실제로 값이 작은 수들끼리 먼저 곱하면 cpu 가속화를 유도하는가라는 의문도 있었는데 이에 대한 반례 실험을 할 필요가 있다. 그냥 단순히 min-heap가 아닌 max-heap를 구현하여 벤치마킹을 실험해보면 알 수 있을것이다.
시간 복잡도
시간복잡도는 주로 세가지 기준에 따라 최선의 경우인 Big-오메가와 최악의 경우인 Big-오, 평균의 경우인 Big-세타로 분류할 수 있다. 이번 분석에선 최악의 경우를 상정하여 최대의 효율을 보려고 하기 때문에 시간 복잡도 Big-O를 사용할 것이다. 그리고 앞서 말한 BigInt의 곱연산 시간 복잡도까지 생각을 해야 하므로 끝에에서 톰-쿡 알고리즘의 카라슈바 알고리즘 케이스인(k=2) c를 붙이겠다.
반복문으로 팩토리얼 구현하기
가장 처음에 백준에 제출한 문제의 핵심 함수다.
function factorialByLoop(number) {
let num = 1n;
for (let i = 0; i < number; i++) {
num *= BigInt(number - i);
}
return num;
}정석대로 n * ... * (n - i) 의 형태인 단순 반복문의 흐름이다.
이 함수의 시간복잡도는 O(N)이다. 단순 계산은 O(1)이기 때문이다.
배열로 팩토리얼 구현하기
function factorialByReversedArray(number) {
const arr = new Array();
for (let i = number; i >= 0; i--) arr.push(BigInt(i == 0 ? 1 : i));
while (arr.length > 1) {
arr.push(arr.pop() * arr.pop());
}
return arr.pop();
}다른 자료구조(PriorityQueue)와 비교하기 위해 알고리즘 과정을 통일시킬려고 배열화 시켰다.
이 함수의 시간복잡도는 O(N)이다. 삽입과 제거가 pop/push여서 O(1)이기 때문이다.
반전 배열로 팩토리얼 구현하기
function factorialByReversedArray(number) {
const arr = new Array();
for (let i = number; i >= 0; i--) arr.push(BigInt(i == 0 ? 1 : i));
while (arr.length > 1) {
arr.push(arr.pop() * arr.pop());
}
return arr.pop();
}몇가지 시도 이후에 나는 BigInt가 작은 수들끼리 곱할수록 cpu 가속화가 이뤄진단 이론을 증명하기 위해 기존 array의 반례인 reversed-array를 추가했다. 단순히 초기화된 배열의 순서만 반전이니 여전히 O(N)이다.
배열의 개형
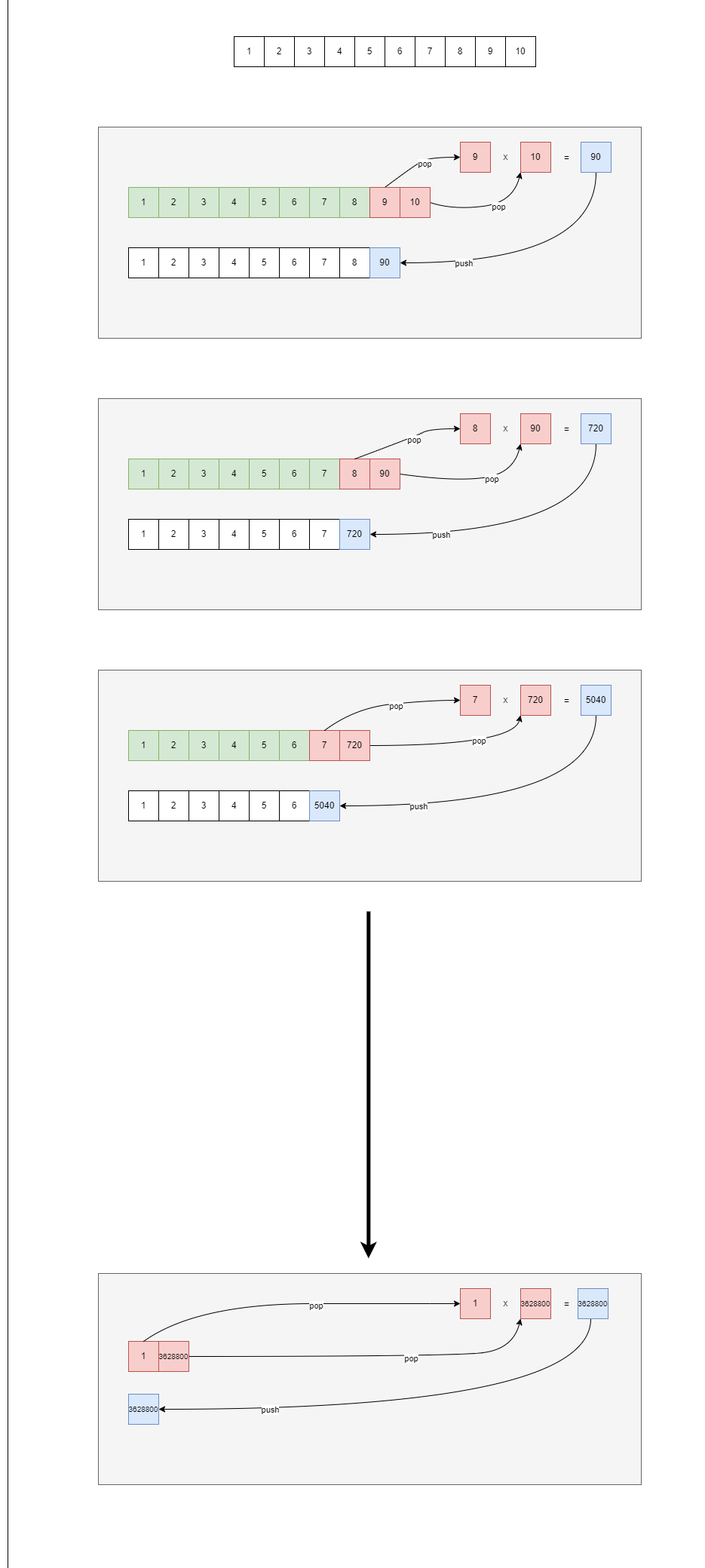
배열은 일반적으로 정렬 여부에 따라 삽입과 삭제에 대한 시간복잡도가 제각각이다.
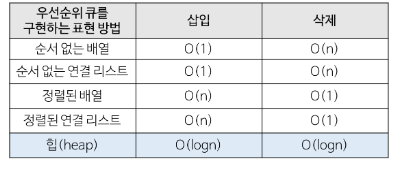
그러나 O(n)이 O(n)인 이유는 대개 중간 삽입 및 삭제를 worst case로 상정해두고 생각해서인데, 이번 구현에선 끝부분에서만 작업이 이뤄지므로 삽입과 삭제가 O(1)임을 알 수 있다.
side note: 자바스크립트의 배열은 근본 배열이 아니다?
자바스크립트 배열은 배열이 아니다, StackOverflow 답변에선 자바스크립트의 배열은 C와 같은 dense array(메모리가 연속적인)가 아닌 spharse array(메모리가 연속적이지 않은)로써 hash table를 기반으로 두고 있다고 한다.

실제로 ChatGPT에게 물어보면 이와 같이 답변하며 첫번째 링크의 블로그 끝부분 테스트에서도 []와 {}에서 배열 인덱스를 키로 두고 제어했을 때의 속도 차이를 설명하고 있다.
side note: 자바스크립트의 배열은 해시 테이블 기반이니 느리다?
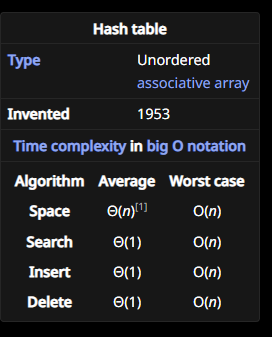
위 의문에 따르면 자바스크립트의 배열은 hash table이란 소린데 hash table 자체의 공간 복잡도는 전부 O(n)이므로 개발자가 기대했던 성능의 n의 곱절은 더 느려져버리는 것이다. 그래서 엔진과 런타임에서 이러한 구조적인 문제를 해결하여 O(1)로 만든 것 같다.
StackOverflow 답변, medium - Time Complexities Of Common Array Operations In JavaScript 그리고 dev - Time complexity Big 0 for Javascript Array methods and examples 와 같은 여러 개발 블로그 및 커뮤니티에서 공통적으로 array의 push와 pop은 O(1)의 시간 복잡도를 가지고 있다고 말한다.
자바스크립트의 배열이 근본은 아니지만 시간복잡도 관점에선 피차일반으로 별 상관이 없음을 알 수 있다.
Min/MaxPriorityQueue로 팩토리얼 구현하기
function factorialByMinHeap(number) {
const queue = new MinPriorityQueue();
for (let i = 0; i <= number; i++) queue.enqueue(BigInt(i == 0 ? 1 : i));
while (queue.heap.length > 1) {
queue.enqueue(queue.dequeue() * queue.dequeue());
}
return queue.dequeue();
}
function factorialByMaxHeap(number) {
const queue = new MaxPriorityQueue();
for (let i = 0; i <= number; i++) queue.enqueue(BigInt(i == 0 ? 1 : i));
while (queue.heap.length > 1) {
queue.enqueue(queue.dequeue() * queue.dequeue());
}
return queue.dequeue();
}각자 min-heap와 max-heap로 구현한 priority queue로 팩토리얼 알고리즘을 구현한 코드다.
이 함수의 시간복잡도는 O(NlbN)이다. 삽입과 제거가 O(lbN)이기 때문이다. 자세한 설명은 아래에서.
Heap이란?
heap은 완전 이진 트리의 일종이 될 수 있는 트리 자료구조 중 하나다. min-heap는 우선순위가 낮은 순서로, max-heap는 높은 순서로 가지가 뻗어나간다. 최소 값과 최대 값을 빠르게 찾을 수 있게 도와주는 힙(Heap) - evan-moon
PriorityQueue이란?
PriorityQueue는 Heap에 기반한 우선순위 큐다. 일반적인 선입선출 구조인 Queue와 달리 Priority Queue는 아이템이 들어오고 나갈 때마다 우선순위에 따라 재배치되는 특징이 있다. 그래서 큐에 값들을 넣고 최솟값 또는 최댓값을 빠르게 꺼내고 싶을 때 유용하다.
PriorityQueue가 factorial 연산에서 반복문에 비해 이점을 취할 땐 Heap로 구현되었을 때밖에 없다. [주의] 왜 우선순위 큐는 배열이나 연결리스트로 구현하지 않을까?
Heap로 PriorityQueue를 구현할 수 있던 방법은 Heap가 인덱스 규칙성을 가지기 때문이다.
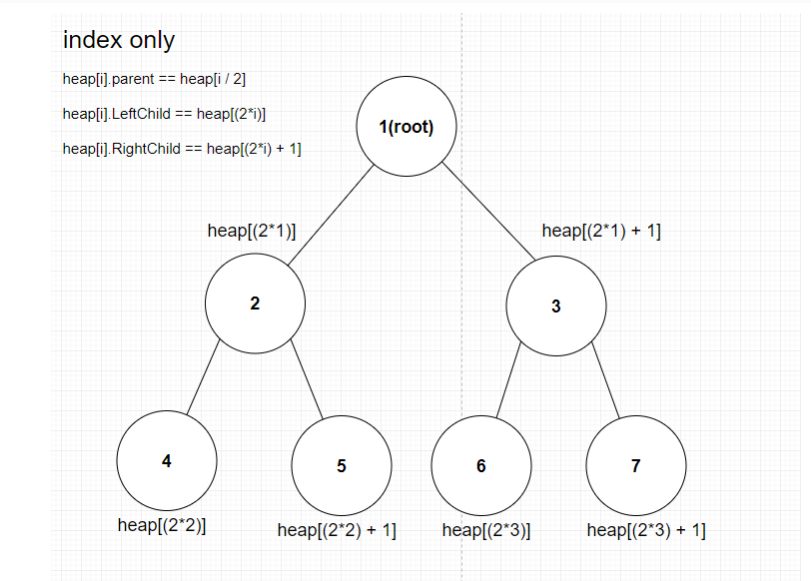
](출처: https://develop-dream.tistory.com/91
min-heap의 개형
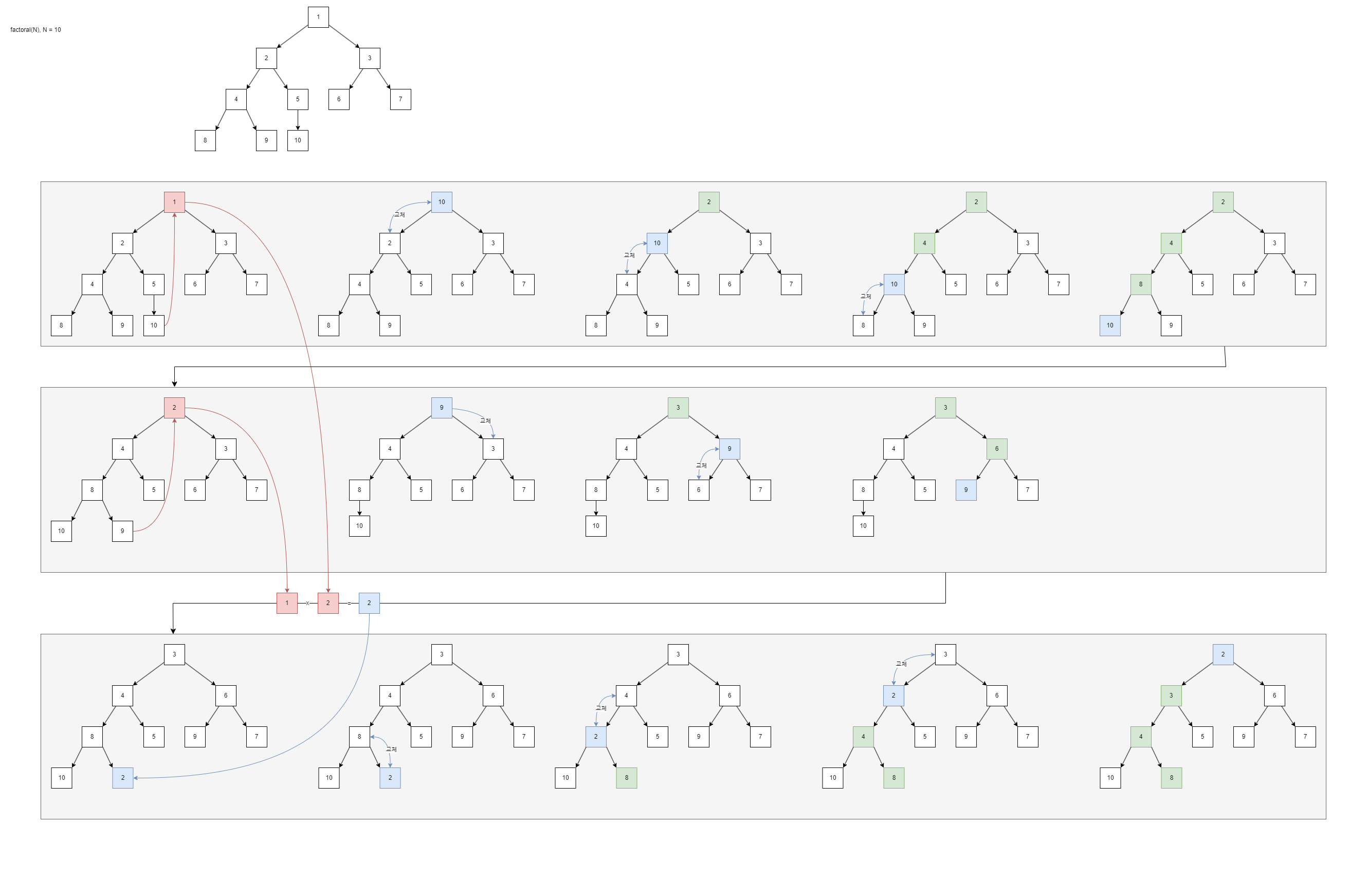
PriorityQueue를 사용한 factorial 함수에서 number에 10을 넣었다고 쳤을 때 while 반목문이 한번 동작할 때의 min-heap 흐름은 위 사진과 같다.
첫번째와 두번째 회색 그룹에서, 함수 dequeue가 호출되어 가장 위에 있는 최솟값이 뽑혀나가고 마지막에 있던 값이 최솟값의 자리로 대체된 다음 min-heap의 규칙에 따라 재조정된다. 이땐 자신 아래에 자신보다 적은 수가 없어야 하므로 재조정 과정에선 자신보다 낮은 수를 찾아 자기 자리(index)와 바꿔치는 작업을 보이는 낮은 수가 없을 때까지 한다.
세번째 회색 그룹에서, 함수 enqueue가 호출되어 주어진 값이 트리의 가장 아래에 주입되고 다시 min-heap의 규칙에 따라 재조정된다. 이땐 자신 위에 자신보다 큰 수가 없어야 하므로 큰 수가 없을 때까지 부모와 자리(index)를 교체한다.
두 함수에서 흥미로운 점은 초록색 박스, 즉 탐색된 아이템이 한 가지(branch) 에 불과하단 점이다. 즉, 모든 아이템이 탐색되는게 아님 이 이 Heap가 취할 수 있는 최대 장점이다. 그럼 BigO를 알아봐야 하는데...
min-heap는 왜 O(log N)일까?
시간 복잡도엔 여러 측정법이 있지만 한가질 뽑자면 worst case, 즉 최악의 가정에서의 시간 복잡도를 기준으로 삼는 Big-O가 있다. 이러한 빅-오 기준에 따르면 위 min-heap의 dequeue 함수에서 최악은 첫번째 회색 그룹, 최악이 아님은 두번째 회색 그룹이라 볼 수 있겠다. 아무튼 최악의 개형을 보자면 최악의 경우인 트리의 끝에 도달하는건, 즉 트리의 높이가 곧 시간복잡도임을 알 수 있다. 그러므로 O(높이)이라 단정지을 수 있으나 BigO 표기법에선 N 하나만 유효하므로 높이를 N으로 계산해야 한다.
이때 logN이 등장한다.
참고: 컴퓨터 과학에서의 logN은 대개 밑이 2인 로그를 뜻한다.
이진적인게 많아서 밑을 2로 두고 사용하는 경향이 생긴 듯 하다. 햇갈릴 여지가 있어서lb를 대신 쓰기도 한다.
시간복잡도에서 등장하는 log는 대개 밑이 2이나 lb가 있을 때의 log는 상수로그일 수 있으므로 유의하자.
층마다 2개씩 갈려나가고 거기서 각 끝부분이 2배로 늘어나는 모습은 2^(높이) 인걸 추측하게 만들어준다. (2 -> 4 -> 8 -> 16) 총량 = 2^높이임을 알았으니 높이가 log2총량임을 알 수 있다. 팩토리얼 함수에서 트리의 총량은 트리의 최댓값이며 최댓값은 곧 주어진 수와 같으니 높이는 log2N이다. 이걸 BigO에 맞춰 바꾸면 lbN이니 결론적으로 min-heap의 BigO 시간복잡도는 O(lbN) 이라 말할 수 있다.
벤치마킹: 각 함수의 시간복잡도
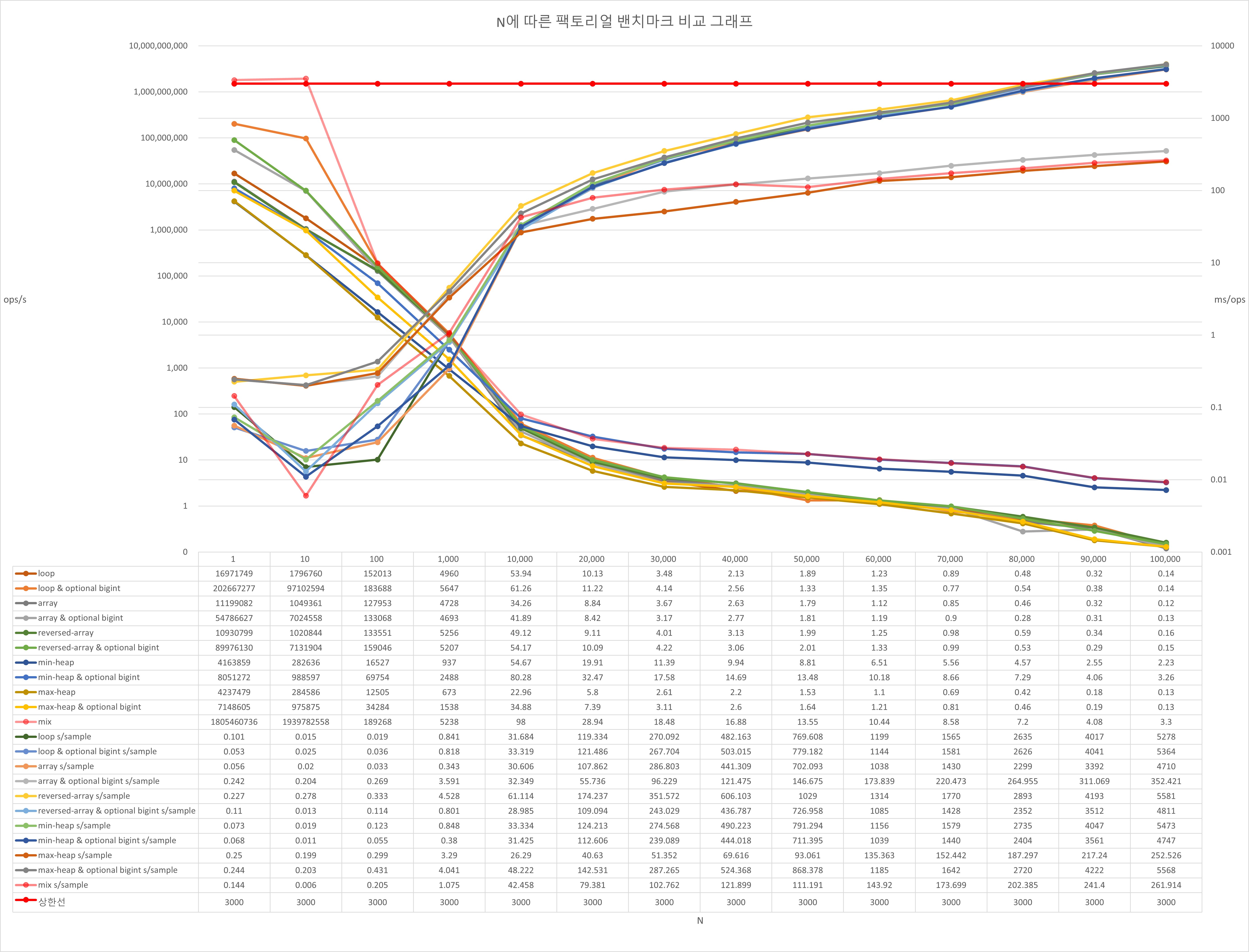
- X축은 팩토리얼 함수에 넣은 파라미터 N, Y축은 걸린 시간(ms)다.
이전 벤치마킹 소스코드 확인하기
새 벤치마킹 프로젝트 확인하기
앞서 말한 작은 수들끼리 먼저 곱하면 cpu 가속화를 유도하는가? 는 아래 사진을 보고 이해할 수 있다.
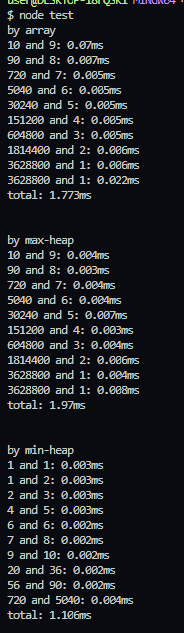
이 사진은 각 함수의 흐름을 확인하기 위해 매 반복마다 출력시키도록 변경한 벤치마킹의 일부 결과다.
array는 "배열의 개형" 문단에서 보여준 다이어그램과 완전히 동일한 순서를 보여주고 있으며 max-heap 또한 큰 숫자들 먼저 꺼내서 넣는 모습을 볼 수 있고 min-heap도 작은 숫자들끼리 먼저 꺼내서 넣는 흐름을 볼 수 있다. 주목해야 할 점은 max-heap와 배열은 소요 시간이 불규칙적이고 비교적 큰 반면 min-heap는 규칙적(linear)이고 비교적 작다는 점이다. 게다가 실제 표를 보면 min-heap만이 그렇지 않다.
Heap의 삽입/삭제는 O(logN)고 Array의 삽입/삭제는 O(1)이므로 이론상 힙이 무조건 느려야 한다. 그러나 이건 삽입/삭제의 속도가 문제가 아니다 min-heap는 BigInt 곱연산의 비-상수 시간복잡도에서 두 수의 격차를 최대한 줄임으로써 N를 최소화한 결과 저렇게 안정적이고 빠른 속도를 생산해낼 수 있다고 생각한다.
그래서 작정하고 배열로 어떻게든 min-heap가 하던 동작을 구현한다면 그게 가장 빠른 알고리즘일 것이다.
side note: 벤치마킹 그래프의 교차점에 관하여
참고: 다른 것들도 다 뇌피셜이지만 이건 근거없는 삘만 가득한 심각한 뇌피셜이다.
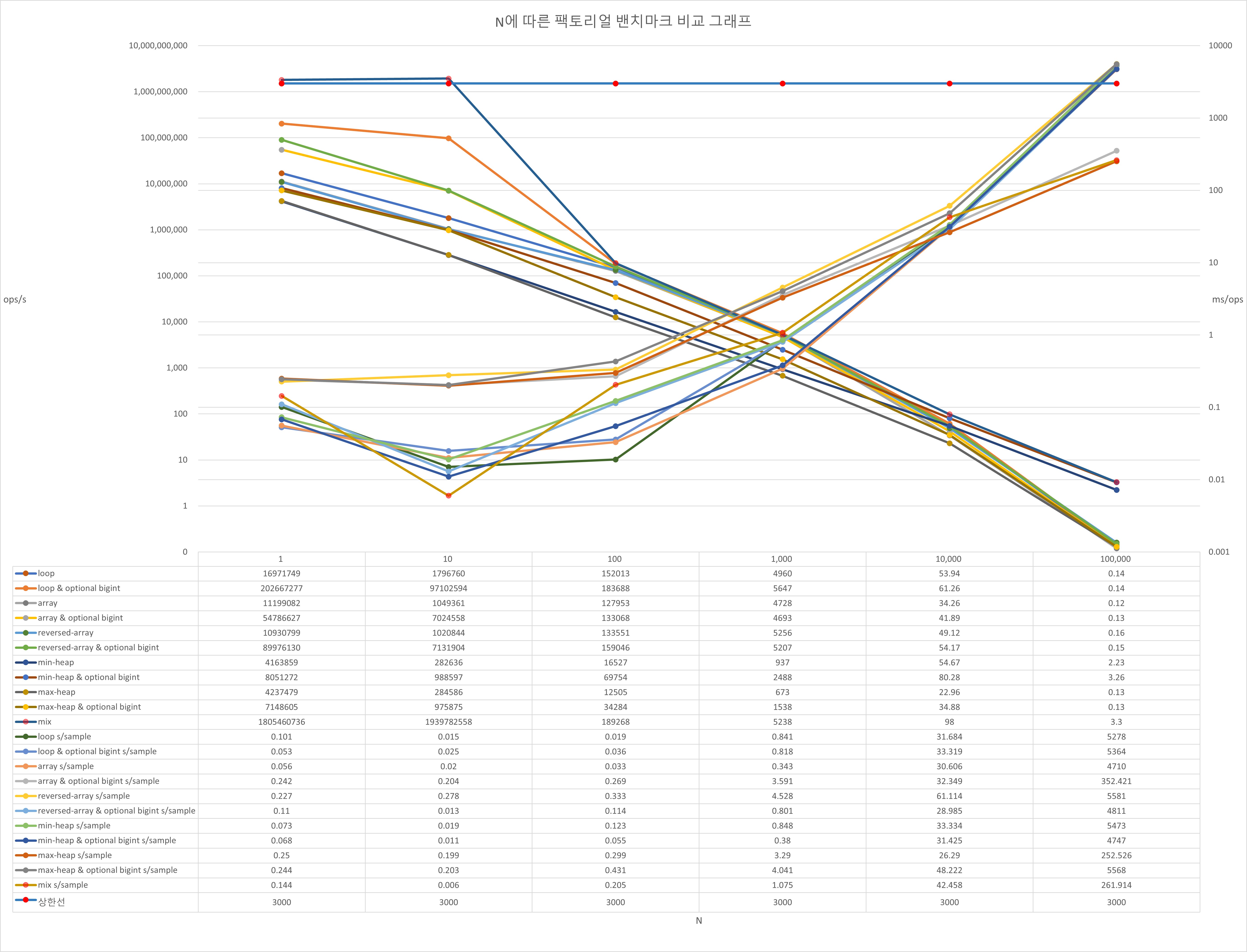
처음 그래프를 보면 교차점 이후가 쭉 늘어진걸 볼 수 있는데, 그건 10000~100000 사이를 다시 10등분하여 측정한 결과이므로 그 부분을 모두 걷어내면 이렇게 지수함수 증가 개형을 볼 수 있다. 그런데 N=10^4를 기준으로 min-heap와 기타 함수들이 서로 효율이 교차되는데 이 특정 지점이 어떠한 의미를 지니고 있는지 시간복잡도 관점에서 이해해보자.
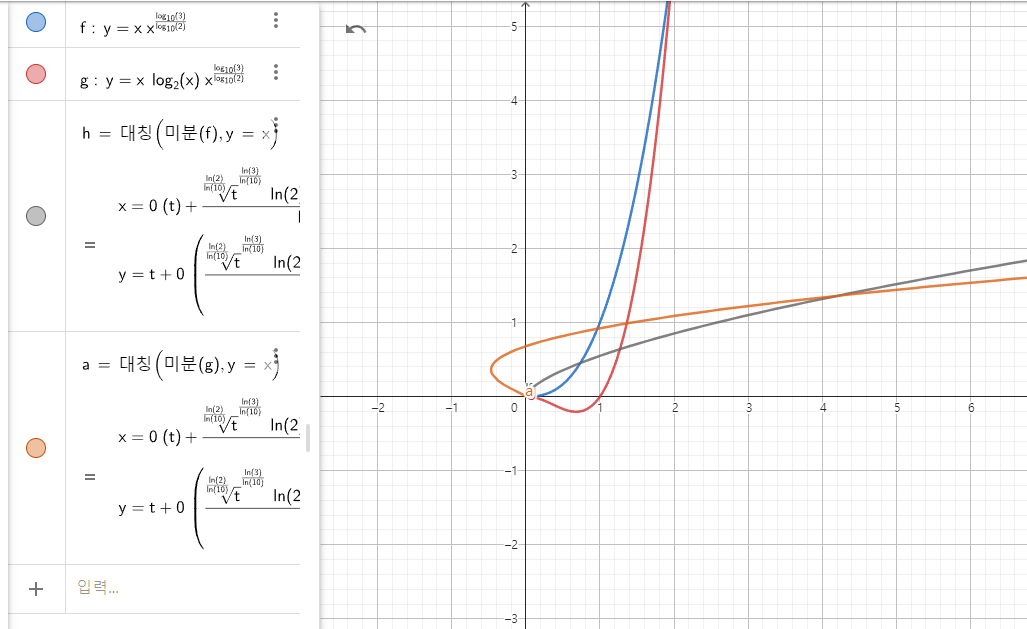
이 그래프는 지오지브라에서 k=2인 톰-훅 알고리즘의 시간복잡도 O(N^(log3/log2))를 선형적으로 n번 반복한 팩토리얼 함수인 f(x)와 반대로 힙을 통해 n번 반복한 팩토리얼 함수인 g(x)를 그리고 그 함수의 미분의 역을 그리고 있다.
일반적으로 시간복잡도란 단위 요소 당 시간이 얼마나 복잡해지는지, 즉 시간 증가량이 얼마나 가파라지는지를 표현한다. 즉 이것이 의미하는 바는 해당 수식의 도함수의 역(미분 역 == 부정적분)을 구하면 그게 곧 그 시간복잡도를 적분하는 것이기에 시간복잡도에 기인한 연속적인 그래프에 부합하다. 이게 그래프에 부합하다고 했을 때 x=4에서 교차점이 보이는건 맨 위 10000(== 10^4)와의 동질감을 느끼게 해주기에 부족함이 없다.
이에 따르면 자바스크립트의 BigInt 곱연산이 카라슈발 알고리즘과 k=2인 톰-쿡 알고리즘 기반인걸 증명할 수 있을 것 같다.
벤치마킹: 극단적인 대소 차이를 지닌 BigInt 곱연산
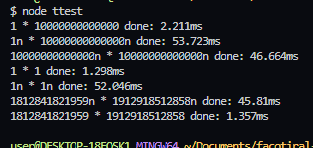
매우 흥미로운 자료다.
첫번째와 두번째 줄을 보면 격차가 심각하게 클 경우엔 bigInt가 오히려 더 느리다.
네번째와 다섯번째 줄을 보면 1n * 1n 끼리의 곱은 십조n와 1n의 곱과 비슷할 정도로 느리다.
이건 어느정도 큰 수인 임의의 13자릿수에도 해당된다.
bigint의 곱은 항상 느린 것처럼 보이나 그건 또 아닌게 애당초 bigint의 곱이 효율을 발휘할 곳(정확히 bigint으로만 존재 가능한 범위)에서 비교군은 존재하지 않다. 그정도로 수가 커지면 자연수로는 곱할 수 없고, 직접 O(N^2)의 다항식으로 bigint를 구현해야 하기 때문이다.
이 데이터가 시사하는 바는 BigInt 문단에서 톰-쿡과 카라슈바 알고리즘, 미디움 블로그에서 공통적으로 말하고 내가 정리한 BigInt의 곱셈은 작은 수에 사용할수록 비효율적이다.를 직접 증명했단 점에서 의미가 있다고 생각한다.
소감
- 최하위 등급의 문제에서 이러한 개념을 깨달은건 굉장히 드문 경험이다.
- 솔직히 이런 노가다 하면서 자료구조를 익힐 줄은 몰랐고 꽤나 놀라웠다.
- 이진트리는 내 생각 이상으로 놀라운 효율성을 지니고 있었다. 혁신적이다.
- 성능보고 벤치마킹해야지 하고 안하는 일이 부지기수했는데 실제로 해보니 재밌었고 흥미로웠다. 추상이 아닌 실체를 보고 본질을 이해하는 과정은 절대 이상적인게 아니였다. 실현 가능한 일이다.
- 팩토리얼 해결법에 subfactorial이나 다른 방법들도 있어보이는데 나중에 여유가 생기면 이것도 다시 봐야겠다.
- 주변인에 따르면 이정도면 플레티넘에 갈법한 것이라 하던데 체감상 골드 내지 실버감인 것 같다. 그런데 다시보니깐 플레티넘이 맞는것 같다.
- 하루종일 여러 사람들과 토론해가며 쓴 글이다. 이를 통해 커피 약 3.5L가 증발했으며 시간 약 40시간이 소요되었다.
- 난생 이렇게 자주 크게 글을 수정하고 갈아엎은 적이 없었다. 애초에 일기장이고 기록장이기에 빈번해지는게 당연한가 싶은데 오히려 역설적으로 이렇게나 열정적이였던 적이 근래에 들어 처음인 것 같다.
- 안타깝지만 정답을 찾지는 못했다. 그래도 가장 가깝고 신빙성있는 이론을 얻어서 많이 기쁘다.
- 아래 출처 및 참고 문단은 이 글을 쓰면서 이해 및 인용 목적으로 조회한 글들의 목록이다. 직접 가서 읽어보는것도 나쁘지 않다고 생각한다.
출처 & 참고
27434번 팩토리얼 3
[주의] 왜 우선순위 큐는 배열이나 연결리스트로 구현하지 않을까?
Priority Queue(우선 순위 큐), Heap(Max Heap, Min Heap)
최소 값과 최대 값을 빠르게 찾을 수 있게 도와주는 힙(Heap) - evan-moon
시간 복잡도 BigO
직접 만든 분석 다이어그램
자바스크립트 배열은 배열이 아니다
StackOverflow - Are JavaScript Arrays actually implemented as arrays?
geeks for geeks - Types of Asymptotic Notations in Complexity Analysis of Algorithms
StackOverflow - JavaScript runtime complexity of Array functions
medium - Time Complexities Of Common Array Operations In JavaScript
dev - Time complexity Big 0 for Javascript Array methods and examples
Hash Table wikiwand
StackOverflow - Hashmaps and Time Complexity [closed]
medium - A fast BigInt.js in an evening, compiling C++ to JavaScript
톰 쿡 알고리즘 wikipidia
카라슈바 알고리즘 wikipidia
JSBI
ECMAScript BigInt proposal
