Binary addition
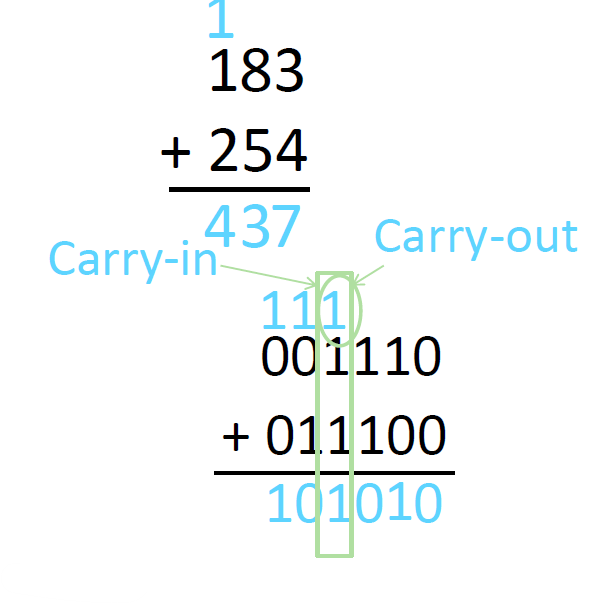
우리가 십진수를 더할 때 각 자릿수의 덧셈이 10을 넘어가면은 10을 다음 자리로 넘긴다. 이진수를 더할 때도 마찬가지이다. 각 자릿수의 덧셈이 2를 넘어가면 다음 자리로 넘긴다. 이때 올림수를 carry라고 하고 덧셈을 해서 carry가 발생했을 때 carry가 나가는 것을 carry out이라고 하고 다음 비트의 연산에서 이전의 비트 연산에서 올림수가 들어오는 것을 carry in이라고 한다.
1-bit Adder(half adder)
1비트를 덧셈하는 덧셈기를 살펴보자. 그런데 half adder이다. 이게 무슨 의미냐면 carry-in이 없는 덧셈기라는 뜻이다.
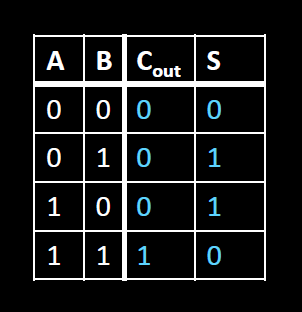
A, B, Cout, S의 값들에 대해서 진리표를 구해보면은 위와 같은 진리표가 나오고
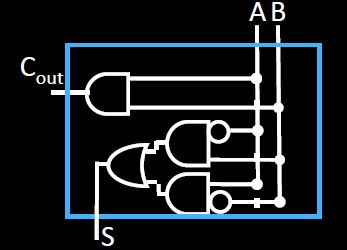
이에 대한 서킷을 구하면은 위와 같다. 위 그림에서 S에서 A, B로 가는 회로는 XOR연산으로 변경이 가능하다.
1-bit Adder(Full Adder)
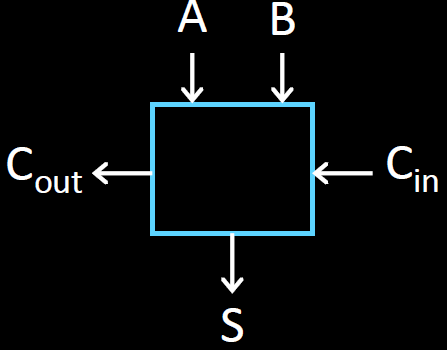
Full Adder는 Carry in이 있는 adder이다.
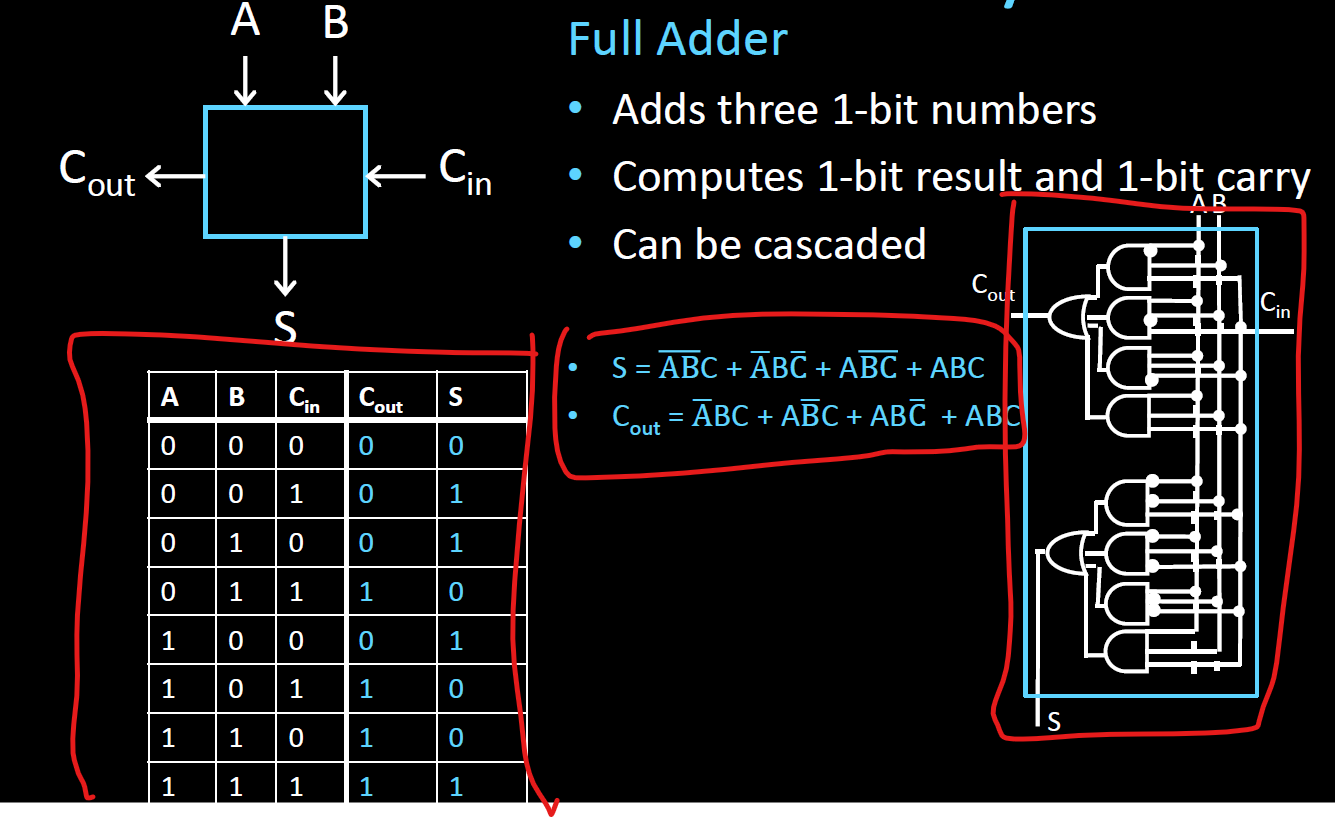
진리표를 구하고 S, Cout을 구하는 서킷을 만들면 위와 같다. 하지만 Sum of products를 구한 결과이다. 더 서킷을 효율적으로 줄일 수 있다.

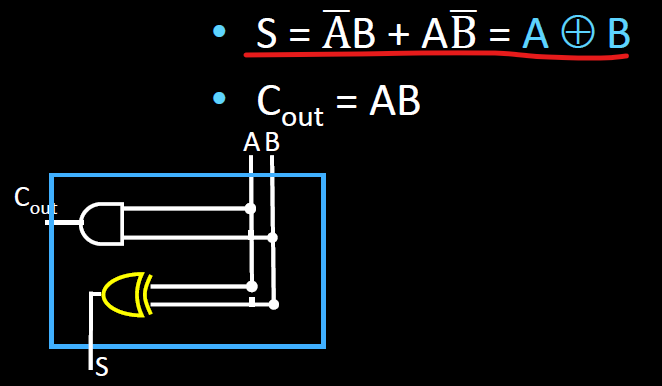
위 그림처럼 XOR연산과 분배 법칙을 이용해서 서킷을 줄인다. 위 그림을 보면 S에서도 Cout에서도 A와 B의 XOR연산을 이용하는데 이렇게 중복되는 부분이 있으면 훨씬 더 효율적으로 서킷을 만들 수 있다.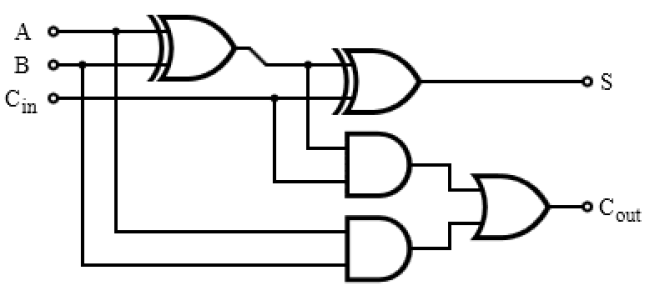
1-bit Adder의 최종 모습이다.
4-bit Adder
자 그러면 4-bit Adder는 어떻게 하면 만들 수 있을까? 바로 1-bit 덧셈기를 이어붙히면 된다.
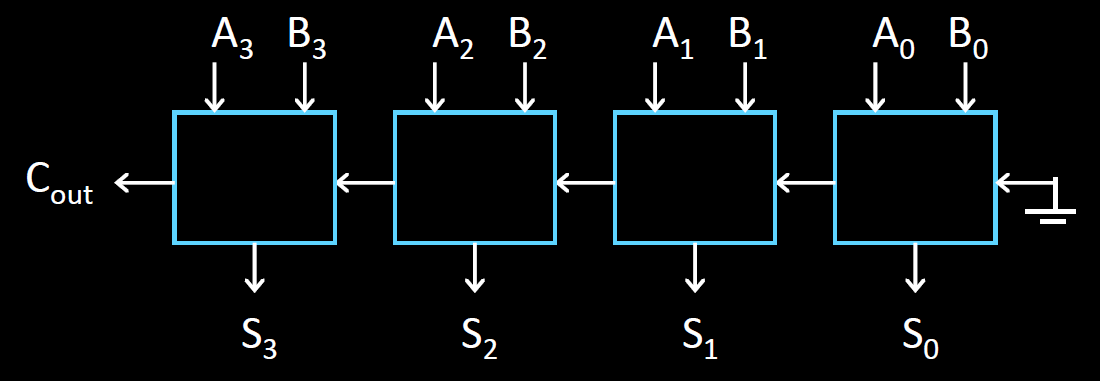
모두 Full Adder를 사용한다. 그리고 첫 덧셈기에 들어오는 carry out은 무조건 0이므로 ground와 연결한다. 이렇게 구성하면 4비트 덧셈기를 구현할 수 있다. 하지만 생각해보자.
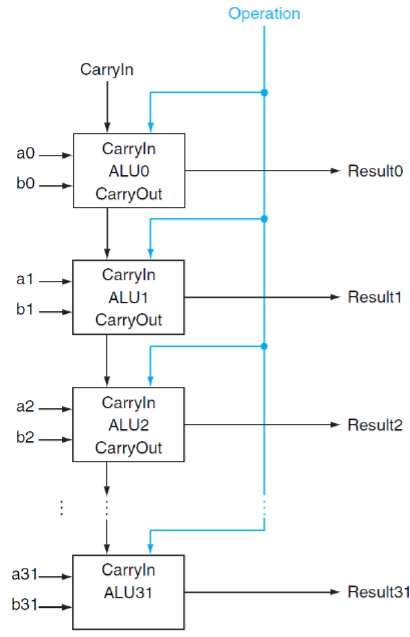
위 그림처럼 덧셈기가 수십개가 연결이 되어있다면? 각 덧셈기는 carry in을 기다려야하기 때문에 연산이 지연되고 index가 높은 덧셈기는 index가 낮은 덧셈기의 연산을 기다려야하고 이는 곧 비효율로 이어진다. 여기서 핵심은 carry in을 기다려야 한다는 점이다.
이를 해결하는 것이 CLA(Caary-Lookahead Adder)이다.
각 carry in을 계산하는 공식을 봐보자.

보다시피 carry in을 C라고 했을 때 C1은 C0에 의존하지 않고 C2도 C1, C0에 의존하지 않는다. 즉, Carry in을 기다려야 하기 때문에 index들은 이전 덧셈기들을 기다려야 하는데 사실 Carry in은 이전 덧셈기 없이도 그냥 계산할 수 있는 것이다! 그래서 이를 활용하면 훨씬 더 효율적으로 N-bit 덧셈기를 구현할 수 있다.
