논리게이트란?

논리 게이트는 디지털 회로에서 불리언 대수를 구현하는 데 사용되는 기본 빌딩 블록 중 하나입니다. 각 논리 게이트는 두 이상의 입력을 받아 하나의 출력을 생성합니다. 출력은 입력에 따라 결정되며, 불리언 대수의 기본 연산 (AND, OR, NOT 등)을 수행하는 함수를 나타냅니다.

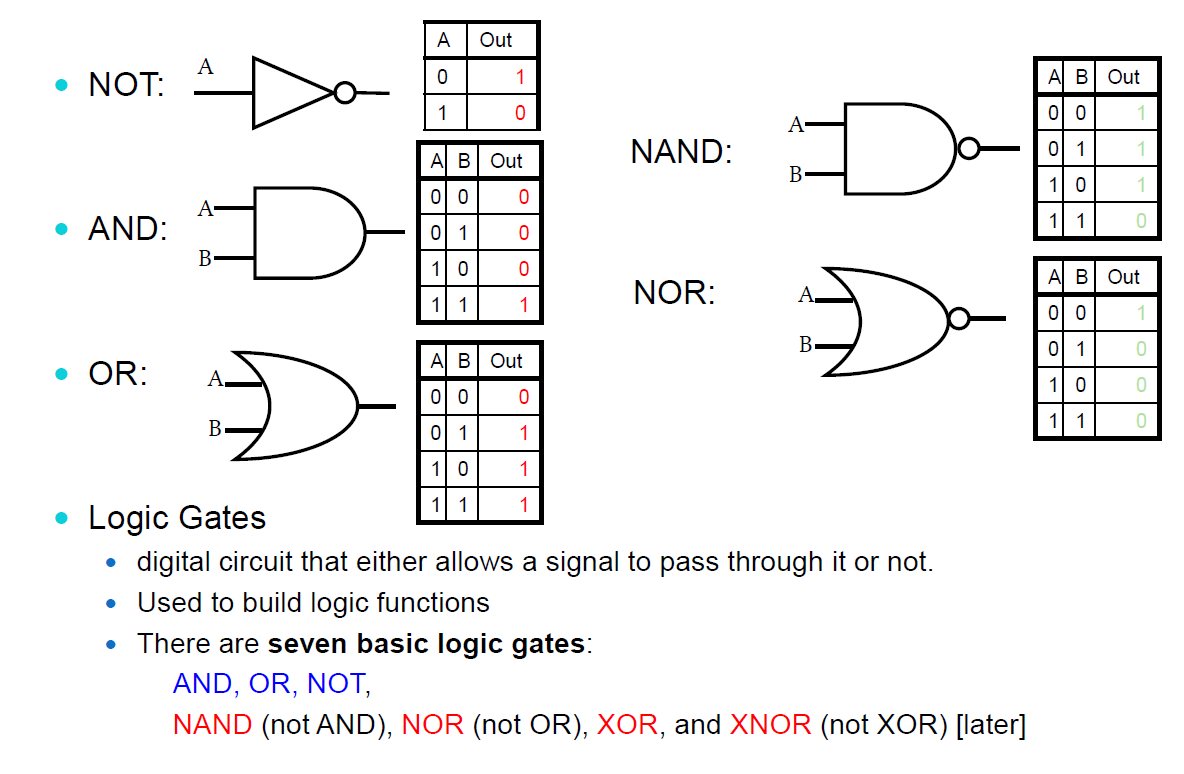
위에서 알 수 있듯이 논리 게이트는 기본적으로 7개가 존재한다. NOT과 AND OR XOR과 각 게이트의 NOT을 붙힌 NOR, NAND, XNOR이다.

XOR

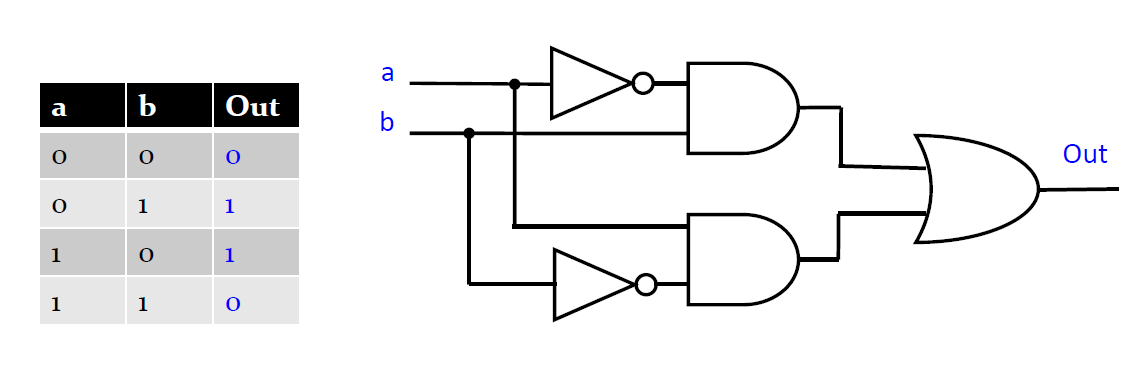
위의 그림에서 a, b에 0과 1을 각각 넣고 나오는 결과를 보면 위 논리 게이트는 XOR연산을 하는 것을 알 수 있다. 그리고 이를 줄여서

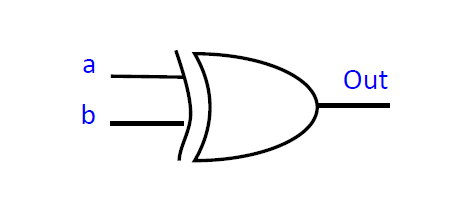
XOR게이트는 위 그림처럼 나타낸다.

Multiplexor

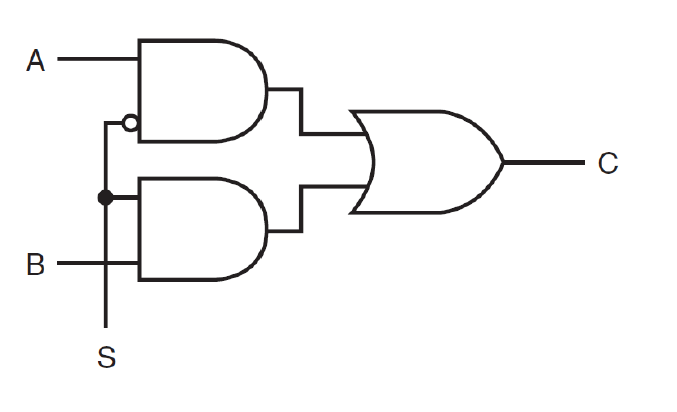
위 그림은 S가 0으로 인가되면은 A의 값에 따라서 C가 결정되고, S가 1로 인가되면은 B의 값에 따라서 C가 결정되는 논리게이트이다. 이를 Multipelxor라고 한다.

Switch-case에 비유를 하자면 A와 B중 한 개를 선택하기 위한 경우로 위 상황을 볼 수 있고, S는 1bit이고 1bit로는 2개의 경우만을 표현할 수 있다. 그래서 위처럼 2가지 경우가 아니라 여러 개의 경우가 있을 때는 S를 구성하는 비트가 한 개가 아니라 여러 개이어야 한다.

이렇게 Multiplexor를 줄여서 Mux라고도 한다.

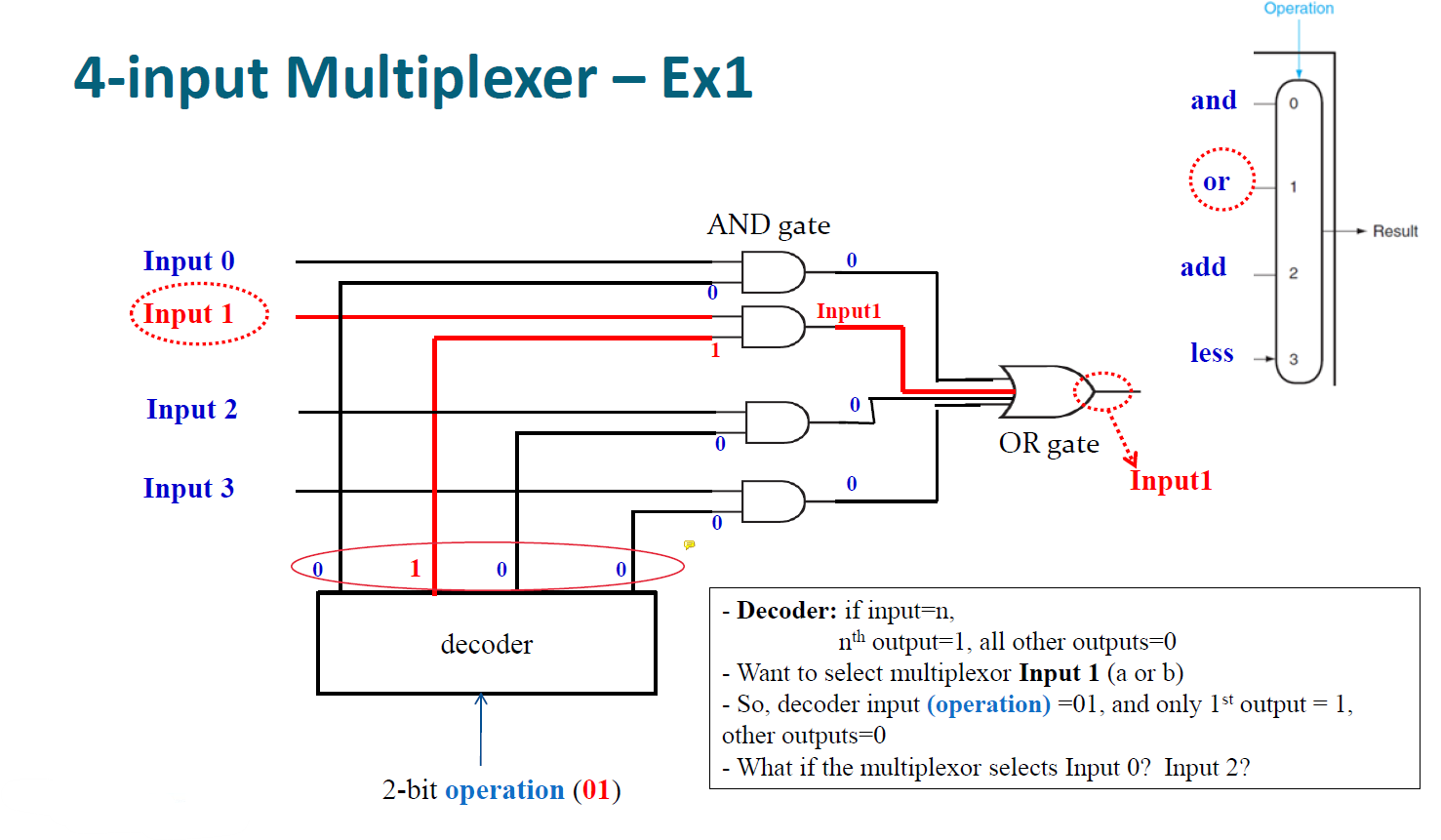
위처럼 input이 4개일 경우에는 2개의 bit로 경우를 표현해야 한다. and 연산을 0으로 매핑, or은 1로 매핑, add는 2로 매핑, less는 3으로 매핑해서 어떤 연산을 할 건지는 S값을 조정해서 결정할 수 있다.

---

논리 게이트를 구성하는데 Logic Circuit을 최대한 효율적으로 만들어야 한다. 같은 결과를 내는 논리 게이트는 여러 개고 그 중에서 가장 효율적인 것을 골라서 사용해야 리소스가 절약되기 때문이다.

논리 게이트 구하기

위 그림에서 왼쪽 게이트와 오른쪽 게이트는 논리적으로 정확히 똑같은 동작을 한다. 하지만 왼쪽은 6개의 게이트를, 오른쪽은 5개를 사용한다. 이렇게 논리 게이트의 수를 줄일 수 있다.

위처럼 algebraic reductions(분배 법칙, 드모르간 법칙)을 이용해서 항의 수를 줄일 수 있다.

Sum of products

Truth table을 통해서 논리 게이트를 구할 수 있다.

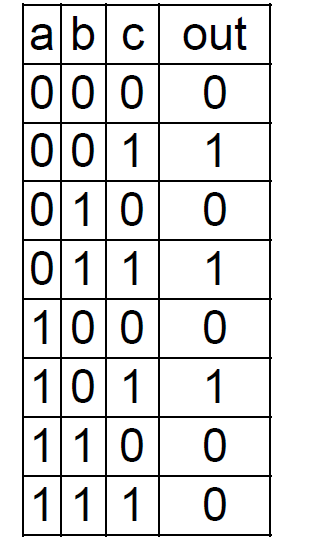
위와 같은 truth table이 주어졌을 때, NOT, AND연산만을 이용해서 input으로 주어진 값을 true로 만드는 논리값들을 구하는 것이다.

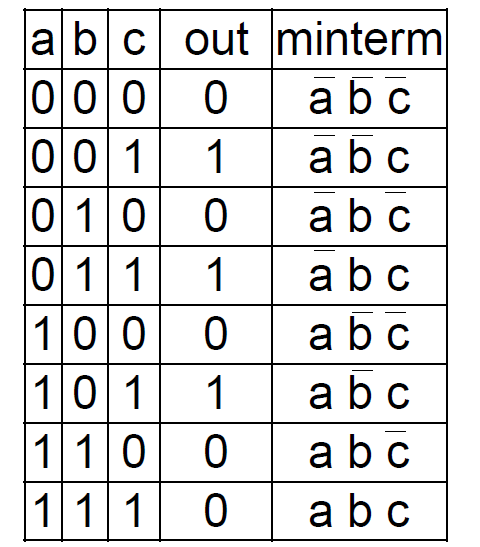
그러면 위처럼 minterm을 구할 수 있고 여기서 out이 1인 minterm을 모두 더하면은 논리 게이트가 완성된다.

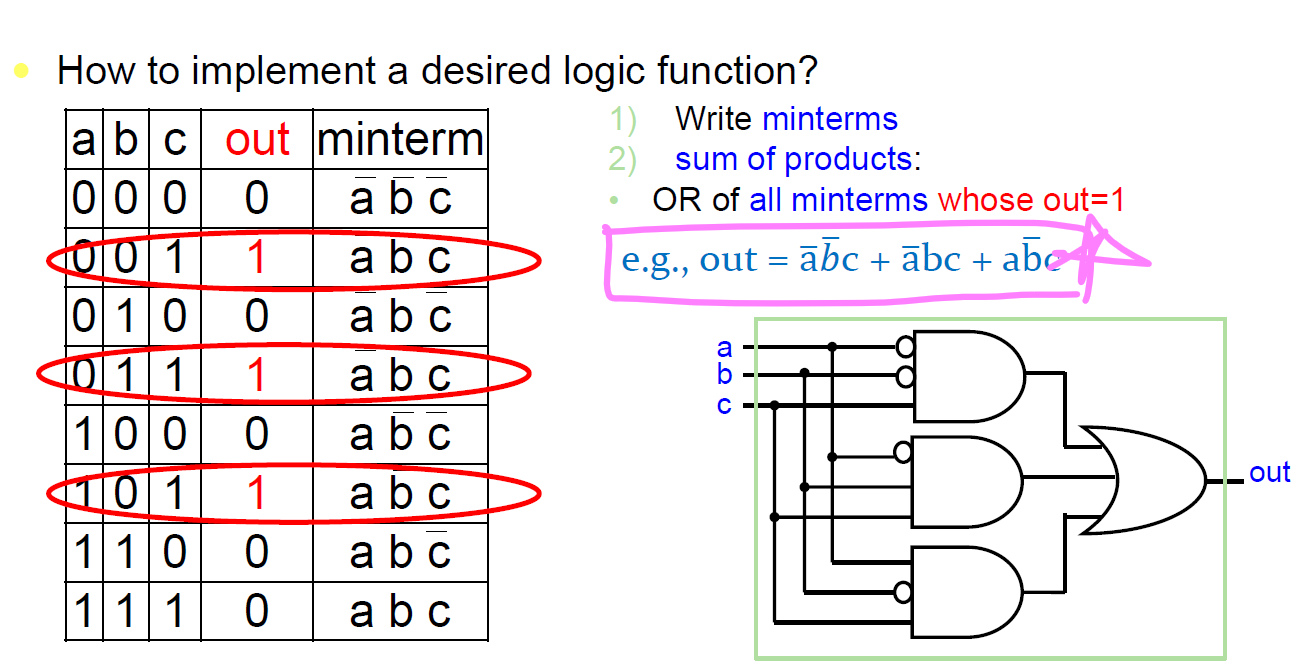
이를 두고 Sum of products 라고 한다. 하지만 이를 product of sums로 바꿀 수도 있다. Sum of products에 not 연산을 2번 한다음 내부의 not연산만 수행을 하면은 product of sums로 내부가 변경된다.

Karnaugh Maps

아주 큰 규모의 서킷, CPU나 AI연산을 하는 TPU 연산을 게이트로 만들 때 사용된다.

방법은 다음과 같다.

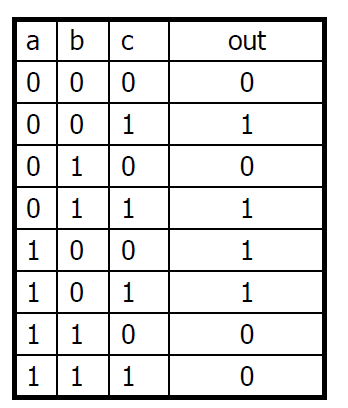
위와 같은 표가 있다고 가정했을 때 input값들을 묶어서 하나의 행열테이블을 만든다.

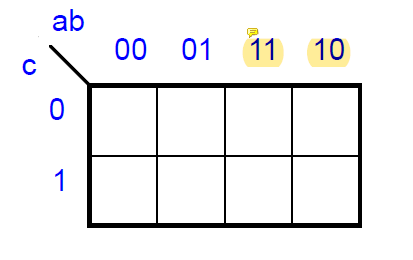
위와 같이 행렬 테이블을 만드는데 행을 자세히 보면은 00 01 10 11이 아니라 00 01 11 10임을 알 수 있다. 이렇게 코드를 작성하는 것을 두고 Gray-coding이라고 하는데 한 번에 한 자리 수만 변하게 하기 위해 이렇게 코드를 작성한다.

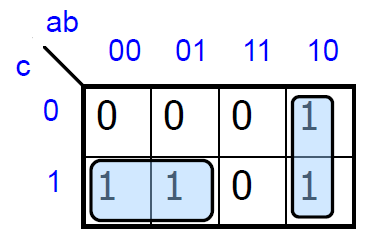
공백칸에 out값을 적으면은 위와 같은 표가 나오는데 2의 power값으로 rectangle을 묶는다. 1의 값들을 묶었을 때 값이 중복되어도 상관없지만, 묶을 때 최대한 큰 직사각형을 묶는 것이 좋다.

두 직사각형 중에 왼쪽을 먼저 보자. b값을 0, 1 둘 중 어떤게 와도 상관없으니 b는 논리연산에 영향을 주지 않는다. 그리고 a는 0이고 c는 1이다. 그래서 a와 c를 and했을 때 1이 나오게 하려면 !ac이어야 한다.
오른쪽을 보면은 c의 값이 0이던 1이던 상관이 없으니 c는 논리 연산에 영향을 주지 않는다. 그리고 a는 1이고 b는 0이므로 둘을 and연산해서 1이 나오려면 a!b이어야 한다. 그래서 결과는 !ac + a!b이다.

이렇게 2의 power의 수를 갖는 직사각형을 찾은 다음에 각 직사각형을 만들기 위한 논리값들을 and연산으로 묶고 각 직사각형들을 sum하는 것이 카르노의 맵이다.

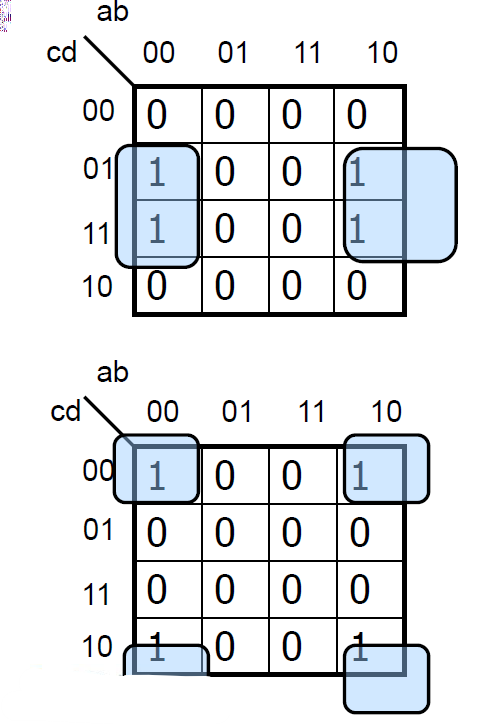
위 두 가지의 경우를 봐보자. 직사각형이 저렇게 나눠져야 할까? 아니다. 첫번째 그림을 보면, 00과 10은 사실 붙어있다. 그래서 ab가 10인 열을 00 옆으로 붙혀주면은 정사각형 하나가 만들어져서 결국 사각형은 1개이다. 아래의 그림도 마찬가지이다.

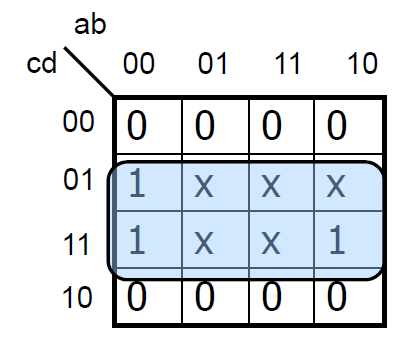
위 그림처럼 x로 적힌 것을 Don't care이다. 무슨 값이 오던 간에 신경쓰지 않겠다는 뜻이다. 우리는 필요 시에는 1로 간주하고 필요없으면 0으로 간주해서 직사각형의 수가 최소가 되게 묶어주면 된다.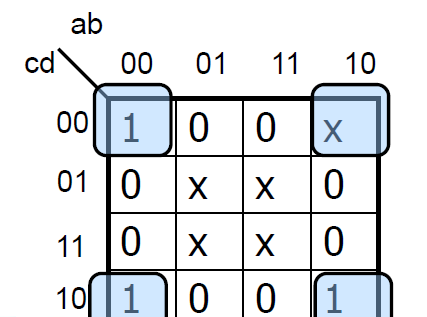
위 그림의 경우에서 가운데 4개의 x는 0으로 간주하면 된다.

트랜지스터에 대한 이해

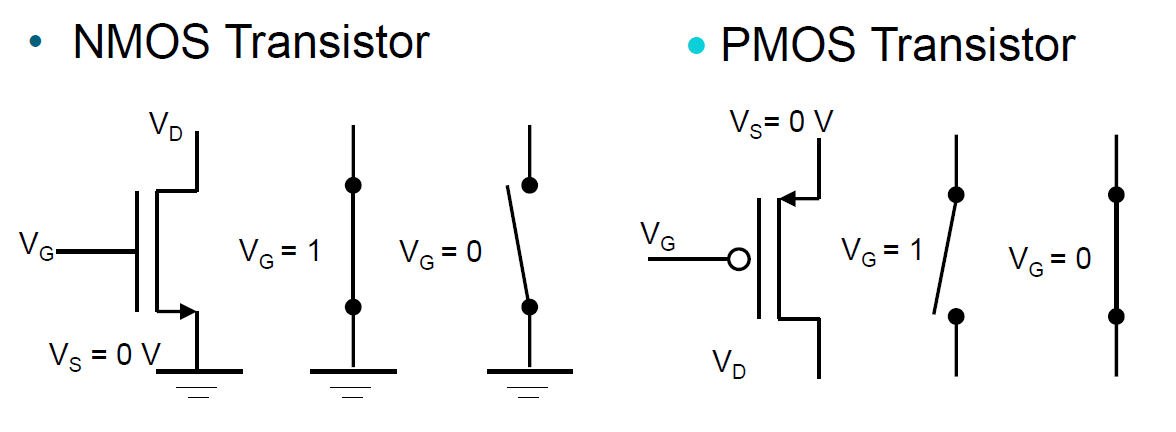
트렌지스터 중에는 NMOS, PMOS가 있다.
그림에서 Vd는 드레인, Vg는 게이트, Vs는 소스라고 한다. Vg에 어떤 값이 인가되냐에 따라서 길이 닫히기도, 열리기도 한다.

NMOS는 Vg가 1로 인가되면은 열리고 PMOS는 0으로 인가되야 열린다. PMOS는 NMOS에 NOT게이트가 붙어있는 형태이다.

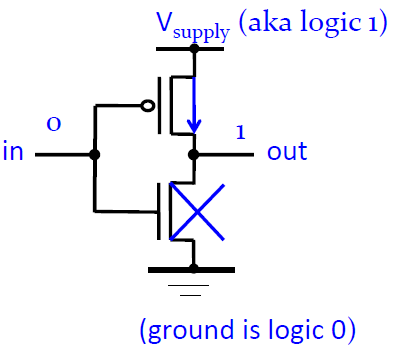
위 그림은 NOT연산을 하는 Invertor을 PMOS, NMOS로 구현한 못브이다. in이 0으로 인가가 되면은 위의 PMOS가 길을 열고 밑의 NMOS는 길을 닫아서 Vsupply에서 값이 1이 공급된다.(ground에서는 0이 공급된다.) 그러면 in은 0이고 out은 1인 not연산을 구현할 수 있다.

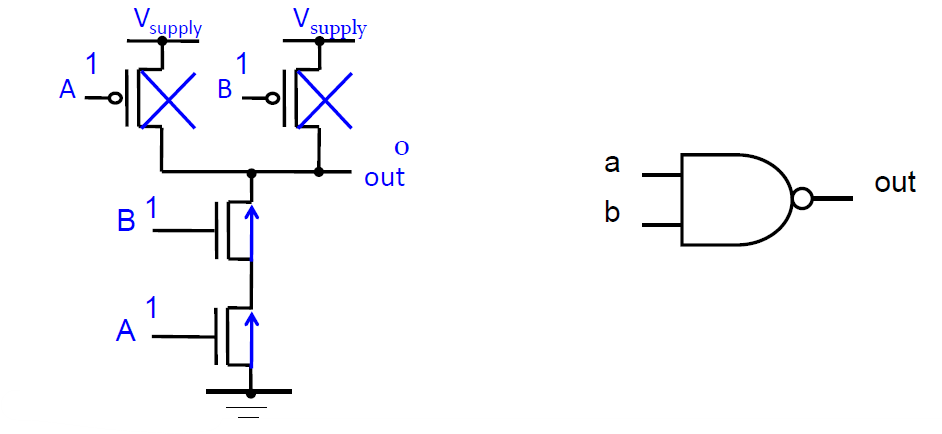
위 그림은 NAND게이트를 구현한 모습이다.

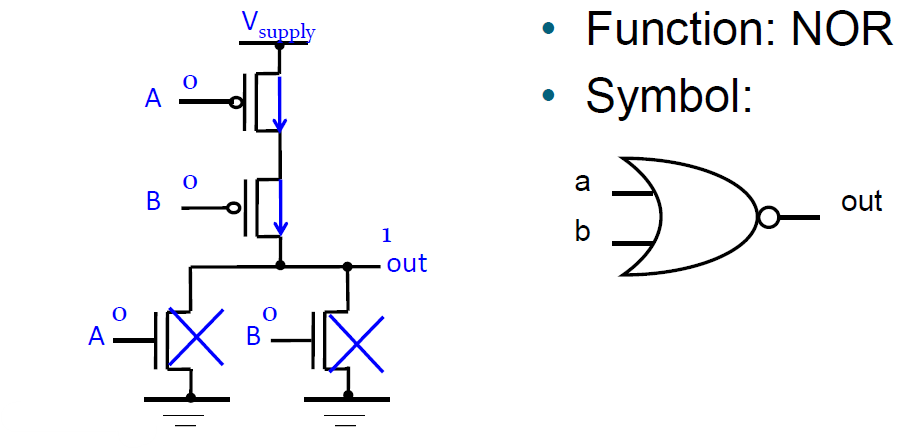
위 그림은 NOR게이트를 구현한 모습이다.

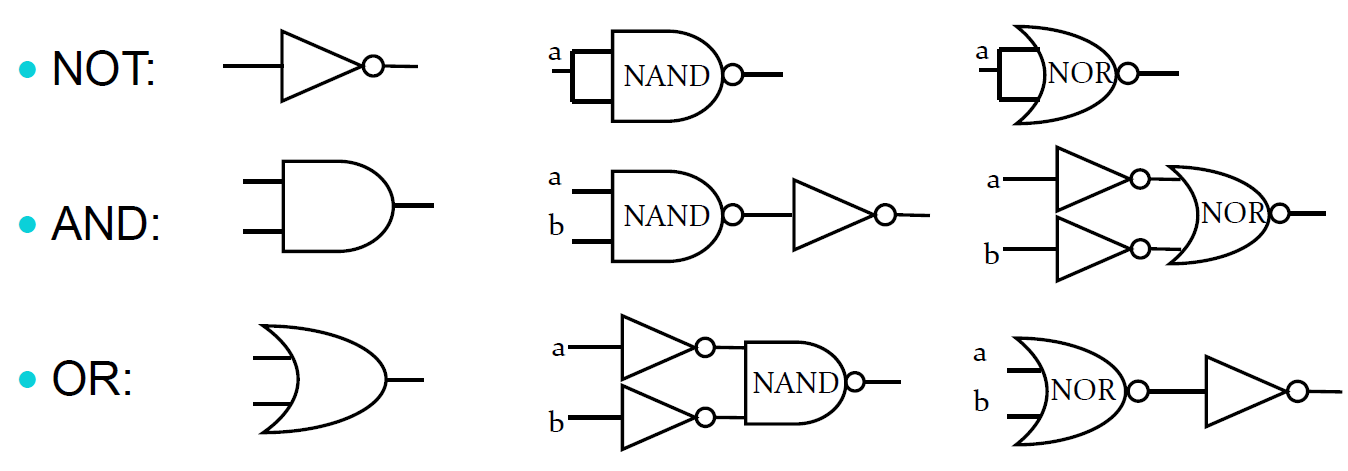
NAND, NOR게이트를 이용하면은 위와 같이 NOT도 만들 수 있고 AND, OR도 만들 수 있다. 이렇게 NAND, NOR을 이용하면은 모든 게이트를 만들 수 있기 때문에 이 둘을 universal하다고 말을 한다.