들어가며
직전 게시글에서 ALU의 구조에 대해서 알아보았다. 모든 논리연산을 구현할 수 있고 덧셈과 뺄셈을 할 수도 있다. 그러면 곱셈과 나눗셈은 어떻게 ALU를 이용해서 구현할 수 있을까?
곱셈기
곱셈의 원리
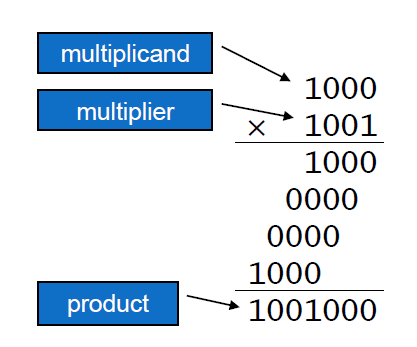
먼저 용어부터 정리해보자.
곱해지는 수를 Multiplicand, 곱하는 수를 Multiplier, 결과를 Product라고 한다.
곱셈은 사실 덧셈의 sum이다. multiplier의 각 자릿수의 값이 0이냐 1이냐에 따라서 덧셈을 하고 말고를 결정해서 곱셈을 구현할 수 있다.
Multiplier의 첫째 자리가 1이라면 product에 multiplicand를 그대로 더하고 둘째 자리가 1이라면 product에 multiplicand를 1자리 LSL연산을 수행해서 더한다.
Multiplier의 N번째 자리가 1이라면 product에 multiplicand를 N-1자리 LSL연산을 수행해서 더하는 방식이다.
곱셈기 - 비효율
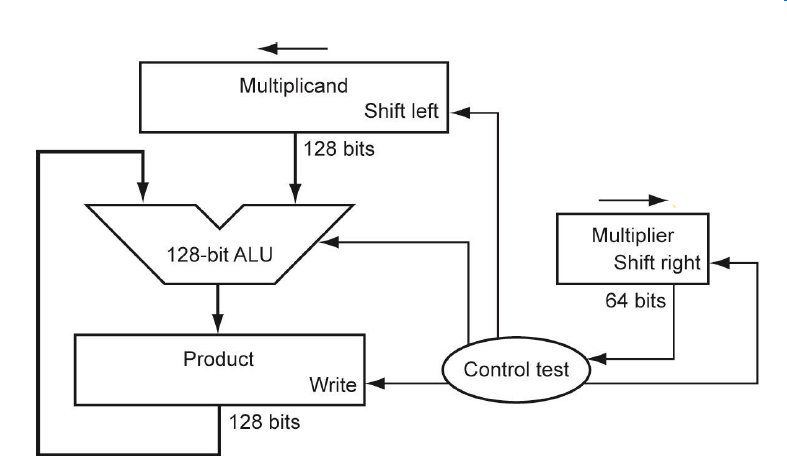
먼저 가장 기본적인 곱셈기의 모습이다. 구성 요소에 대해서 먼저 살펴보면 Multiplicand는 128 비트 레지스터에 저장된다. 왜냐하면 Multiplier의 N번째 자리가 1이라면 Multiplicand를 N-1의 LSL연산을 수행하는 것을 한다고 했는데 N-1번의 LSL연산을 감당해야하기 때문에 64비트 곱셈에서 128비트의 레지스터가 피룡한 것이다.
그리고 결과값이 128비트 이므로 Product도 128비트 레지스터에 저장되고 사용되는 덧셈기도 128비트 ALU이다.
Control Test는 Multiplier의 LSB가 0인지 1인지를 판단한다. 0이면은 No operation, 1이면은 Product에 Multiplicand를 더한다.
곱셈의 원리는 다음과 같다.
- Multiplicnad를 오른쪽 64비트에 저장하고, Product를 0으로 초기화한다.
- Multiplier의 LSB를 확인한다.
2-1. 1이면은 Product에 Multiplicnad를 더한다.
2-2. 0이면은 No operation - Multiplicand를 1비트 LSL하고 Multiplier를 1비트 LSR한다.
- 연산횟수가 64회 미만이면 2번으로 돌아간다.
- 종료
하지만 이는 비효율적이다. 좀 더 효율적인 곱셈기를 알아보자.
곱셈기 - 효율
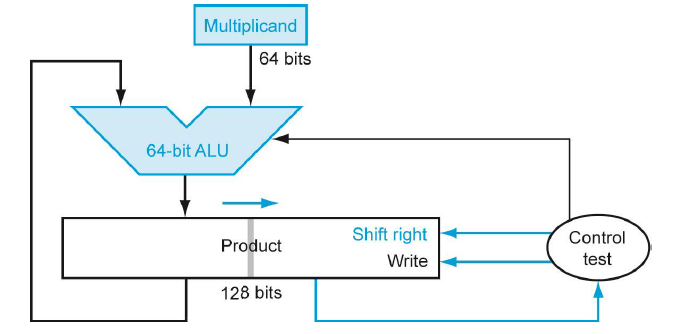
Multiplier과 Product를 하나의 레지스터에 넣어버린 모습이다. 그리고 이제는 Multiplicand를 LSL하는게 아니라 Product를 LSR을 해서 자릿수에 따른 다른 연산을 수행한다.
위 구조에서 초기에는 128비트의 레지스터의 왼쪽 64비트에는 Product가, 오른쪽 64비트의 Multiplier가 위치한다. Control Test는 레지스터의 LSB를 확인해서 덧셈을 할지 말지를 결정한다.
위 구조에서 곱셈의 과정은 다음과 같다.
- 레지스터의 왼쪽을 0으로 초기화, 오른쪽을 Multiplier로 초기화한다.
- 레지스터의 LSB를 확인한다.
2-1. 1이면은 multiplicand를 오른쪽 64비트에 더한다.
2-2. 0이면은 No operation - 레지스터는 1비트 LSR한다.
- 64번 미만 수행했으면 2번으로 돌아간다.
- 종료
전체적인 흐름은 별반 다르지 않다. 하지만 일단 사용되는 레지스터를 하나 줄였다. 그리고 이전 버전은 Multiplier를 LSR하고 Multiplicand를 LSL했다. 즉, 연산을 2번했는데 여기서는 Multiplier과 product를 동시에 LSR하는 연산으로 연산을 1회 줄였다. 전체적으로 보면 64회를 줄인 것이다. 이러면 64비트 곱셈에서는 총 64회의 루프가 돌면된다.
Fast Multiplier
그런데 사실 덧셈은 1회의 연산이면 되는데 곱셈은 64회나 필요하다.
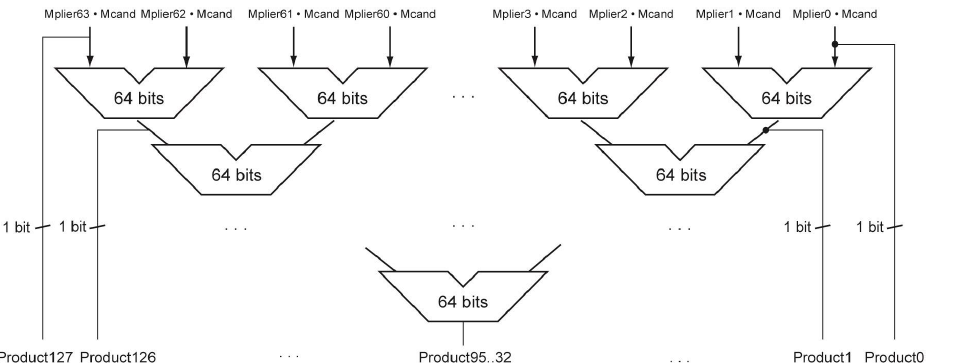
그래서 위 그림처럼 ALU를 트리 구조로 배치해서 연산을 좀 더 빠르게 수행하게 할 수 있다. N비트 곱셈을 한다 했을 때 트리의 높이는 Log2(N)이다.
곱셈 명령어
- MUL: 곱셈 결과의 오른쪽 64비트를 제공한다.
- SMULH: sigend 곱셈의 왼쪽 64비트를 제공한다.
- UMULH: unsigend 곱셈의 왼쪽 64비트를 제공한다.
하나의 레지스터가 가지고 있을 수 있는 최대 비트는 64비트이다. 그래서 곱셈의 결과가 64비트를 넘어가면 오버플로우이다. 이는 SMULH나 UMULH의 값으로 오버플로우를 확인할 수 있다. SMULH, UMULH의 값이 0이 아니라면 오버플로우가 발생한 거고 곱셈의 값을 표현하기 위해 2개 이상의 레지스터가 필요하다는 뜻이다.
나눗셈기
나눗셈의 원리
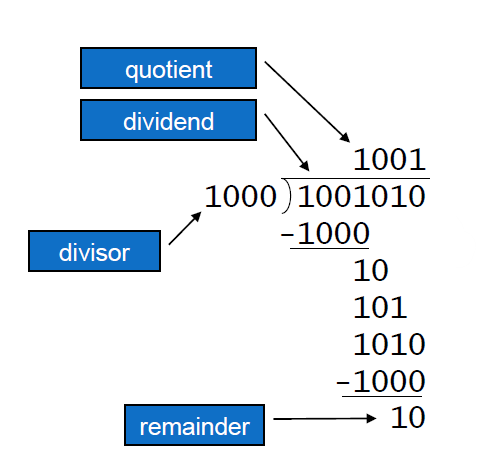
용어를 먼저 정리하자.
나눠지는 수를 dividend, 나누는 수를 divisor, 몫을 quotient, 나머지를 remainder라고 한다.
우리가 뺄셈을 할 때는 dividend의 MSB와 divisor를 비교한다. diviend가 더 크면 뺀다. 그렇지 않으면은 diviend의 MSB를 보는 것이 아니라 그 다음 비트까지도 확인을 한다. 이 원리를 이용해서 나눗셈기를 구현할 수 있다.
나눗셈기 - 비효율
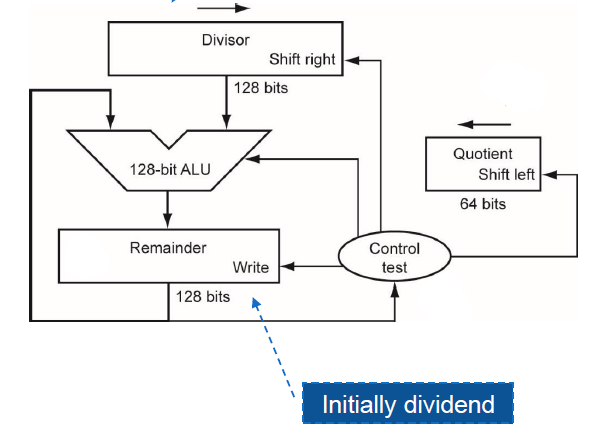
위는 나눗셈기의 모습이다. 일단 나눗셈기의 특징부터 말하자면 곱셈기는 N비트 곱셈에는 N번의 반복이 필요했다. 근데 나눗셈기는 N+1번의 반복이 필요하다. 왜인지 알아보자.
먼저 원리는 Remainder에 최초로 dividend를 초기화한다. 그리고 remainder에서 divisor을 뺀다. 그러면 Control Test는 연산값이 양수인지 음수인지를 판단하다. 음수라면 뺄 수 없는 건데 뺀 거니까 원상복귀한다. 양수라면 Quotient를 1비트 LSL하고 LSB에 1을 기입한다. 음수여도 동일하게 Quotient를 1비트 LSL하고 LSB에는 0을 기입한다.
요약하자면 다음과 같다.
- Divisor를 오른쪽 64비트에 초기화하고 remainder에 dividend를 초기화한다.
- remainder에 divisor를 뺀다.
2-1. 음수라면 원상복구 시키고 Quotient를 1비트 LSL한다.
2-2. 양수라면 Quotient를 1비트 LSL하고 LSB를 1로 변경한다. - Divisor를 1비트 LSR한다.
- 65회 미만 연산 시 2번으로 돌아간다.
- 종료
나눗셈기 - 효율
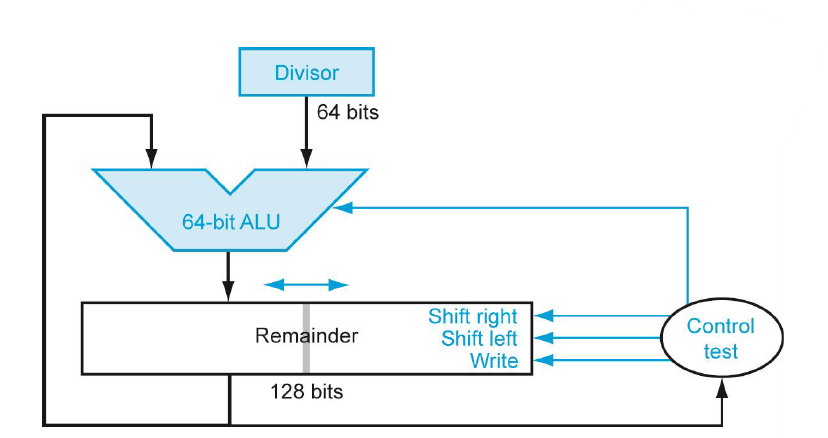
위 그림은 나눗셈기를 효율적으로 나타낸 모습이다. 이전에 곱셈기 효율 버전이랑 생긴게 비슷하다.
비효율 버전에서는 divisor를 LSR하고 Quotient를 LSL했다면, 이제는 remainder과 Quotient를 합쳐서 둘을 한 번에 LSL하는 방식으로 변경됐다.
또 기존에는 divisor을 LSR하는 방식을 이제는 remainder를 LSL하는 방식으로 변경했다.
원리는 다음과 같다.
- 레지스터의 오른쪽 64비트를 dividend로 초기화한다.
- 레지스터의 왼쪽 64비트에 divisor를 뺀다.
2-1. 음수라면 원상복구하고 레지스터를 LSL한다.
2-2. 양수라면 레지스터를 LSL하고 LSB에 1을 적는다. - 65회 미만 연산 시에 2번으로 돌아간다.
- 종료
나눗셈기의 원리도 별반 다르지 않다. 곱셈기나 나눗셈기나 나눠지는 수, 곱해지는 수를 움직이냐 아니면 몫이나 product를 움직이냐의 차이를 둔 것이다.
나눗셈 명령어
- SDIV: sigend 나눗셈
- UDIV: unsigned 나눗셈
divide by zero 에러는 나눗셈기로는 (하드웨어로는) 찾을 수 없다. 이는 소프트웨어의 영역이다.
