들어가며

소수의 표현 및 연산을 어떻게 하는 지 알아보자.

Floating Point Representation

Floating Point는 부동 소수점이라고 하며 소수점이 어느 한 곳에 정해져있지 않고 둥둥 떠다닌다는 의미이다. 후에 배우겠지만 지수부의 값을 변경해서 소수점의 위치를 변경할 수 있다.

scientific notation

과학적 기수법, 과학적 표기법은 너무 크거나 너무 작은 숫자들을 십진법으로 편하게 작성하여 표현하는 방법이다.

쉽게 말해서 우리가 너무 큰 수들을 간단하게 표현하는 방식이다. 가령

1000000000000 = 10^12

로 표현하는 것도 scientific notation이다. 마찬가지로 소수도 이와 같이 표현할 수 있다.

소수를 소수부와 정수부로 나누어서 '특정 소수의 몇 배를 하면 기존의 소수이다' 라는 것을 알려줄 수 있다. 위 그림처럼 소수부의 왼쪽이 1의자리일 경우에는 정규화가 되었고 그렇지 않으면 정규화가 되지 않은 것이다.

Standard

IEEE Std 754 1985 에 의해서 정의되었고 요즘 대부분의 컴퓨터에서는 위 스펙을 따르고 있다.
두 개의 표현식이 있으며

• Single precision : 32비트
• double precision : 64비트

이다.

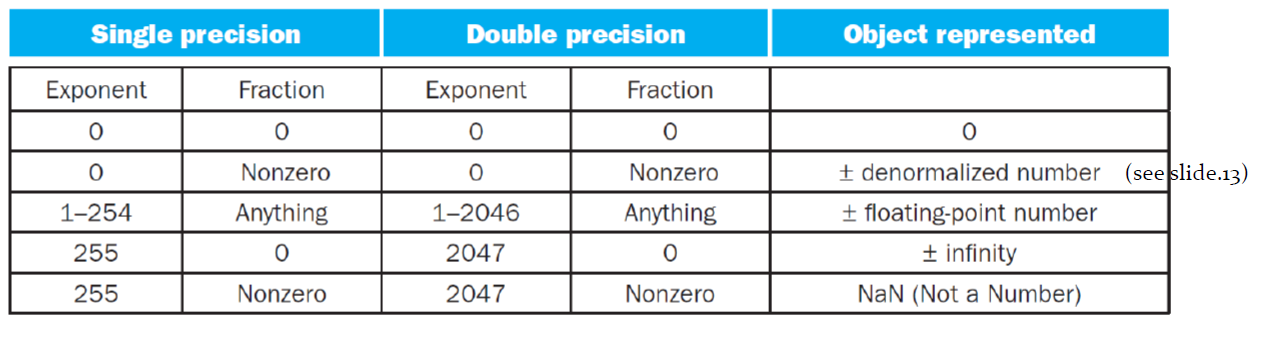
위에서 얘기했다시피 소수는 소수부와 지수부로 나눌 수 있으며 특이 케이스에 대해서 기술해놓은 표이다.
위에서부터 순서대로 표시를 해보면,

1. 지수부, 소수부가 모두 0이면은 0이다.
2. 지수부가 0이고 소수부가 1이면은, 0과 1사이의 아주 작은 수를 표현하기 위함이다.(그 이유는 뒤에서 설명한다.)
3. 일반적인 경우
4. 지수부가 255이고 소수부가 0이면은 무한대를 의미한다.(부호가 있다.)
5. 지수부가 255이고 소수부가 0이 아니라면 NaN을 의미한다.

NaN은 말 그래돌 Inf - Inf 나 0/0처럼 유효하지 않은 연산 결과를 의미한다.

Format

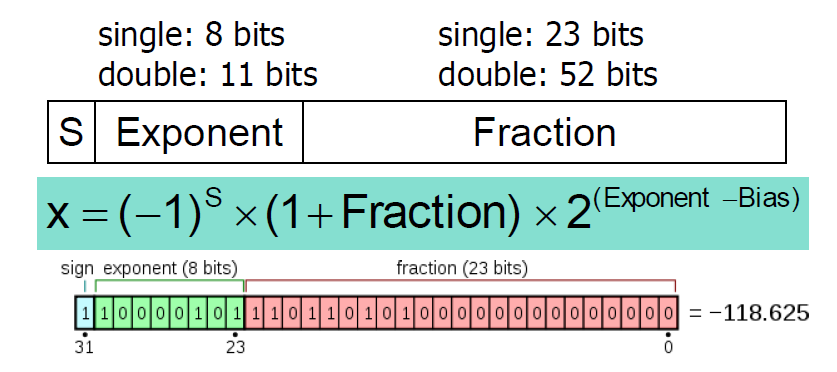
소수의 포멧은 위와 같다. Single precision을 기준으로 MSB는 부호를 의미하고 그 다음 8비트는 지수부, 나머지는 소수부의 소수점을 의미한다.
특이한 점은 소수부를 표현할 때는 1이 더해져있음을 가정한다는 것이다. 즉 Nomalization이 되어있다고 가정한다.
Fraction에는 10진수 소수를 2진수 소수로 변환하고 Nomalization을 했을 때 생기는 소수를 적는다.

또 하나 특이한 점은 Exponent이다. 지수부에는 음수가 들어갈 수도 있지만 Exponent는 unsigend이다. 대신에 bias를 지수부에 더하고 뺴면서 연산을 한다. 그러는 이유는 두 수를 비교할 때 지수부를 좀 더 쉽게 비교하기 위해서이다.

중요한 부분인데, 지수부는 8bit이므로 256개가 표현이 가능하다. signed 기준으로 -128 ~ 127 까지 표현이 되는데 좌우 대칭을 위해서 -128을 이용하지 않는다. 그랬을 떄 값들을 0~으로 맞춰주기 위해서 127을 더하게 되고 이 때 더해지는 127을 bias라고 한다.

위에서 살펴보았듯이 특수한 값들(Inf, NaN 등)을 표현하기 위해서 지수부의 값을 보는데 지수부의 값이 0일때와 최대일 때는 각각 아주 작은 수와 무한대, NaN을 표현하기 위해 사용된다. 그래서 일반적인 실수를 표현하기 위해 허용되는 Exponent의 크기는 1~254이고 127을 빼면은 -126~127까지이다.

Underflow

지수부의 값이 허용되는 범위를 넘어서면은 엄청나게 큰 양수에서 음수로 확 넘어가는 시점이 있다. 그러는 이유는 주어진 8개의 비트로 표현할 수 있는 범위를 넘어섰기 때문인데 이럴 떄는 Overflow라고 하지 않고, 수가 급격하게 작아졌으므로 Underflow라고 한다.

Example

-0.75를 부동소수로 표현하는 과정이다. 먼저 음수이므로 MSB는 1이다.
0.75을 분수로 나타내면 3 / 4이다. 여기서 우리가 주목할 점은 분수에서 분자와 분모를 각각 다르게 이용하자는 것이다.
3은 2진수로 표현하면 11(2)이다. 그리고 1/4는 2^-2이므로 각 수를 지수부 소수부로 표현하면은
-1 11.0(2) 2^-2 이다. 하지만 정규화를 해야하므로 11.0(2)를 1.1(2)로 바꿔줘야하고 이는 10진수로 따졌을 떄 2를 나눈 것이므로 2를 다시 곱해주면 결과적으로
-1 8 1.1(2) 8 2^-1가 된다.

다른 예제이다. 이번엔 부동 소수를 10진수로 표현하는 과정이다.
먼저 MSB가 1이므로 음수이고 뒤에 8자리가 10000001(2)이므로 129이지만 bias를 빼줘야하기 때문에 2이다. 즉 지수부는 2^2이다.
Fraction은 01000... 이므로 위 값들을 실제로 표현하면
-1 (1 + 0.01(2)) 2^2 이다.
여기서 우리가 위 값을 계산하기 위해서는 0.01(2)가 가지는 의미를 알아야 한다.
0.01이 10진수라면 이는 무엇일까? 바로 1을 10^2으로 나눈 것이다. 그러면 0.01(2)는? 1을 2^2로 나눈 값이 된다. 즉 0.01(2)는 10진수로 표현하면 1/4이다.

그래서 위 값들을 계산하면 -1 1.25 4 이므로 5.0이 된다.

Denormal Numbers

Denormal Numbers은 0과 1사이에 있는 아주 작은 값을 뜻한다. Exponent가 0일 경우에는 Denormal Numbers를 표현하는 것으로 Fraction에서 기존에 1 + Fraction(2)에서 1이 사라진다. 즉, 아주 작은 수가 표현이 가능해지는 것이다.

연산 결과는 위와 같으며 Single precision을 기준으로는 Bias는 127이다.

Floating point Arithmetic

add

우리가 소수 덧셈을 할 때는 무엇을 할까? 바로 소수점의 위치를 갖게하고 더한다. 부동 소수의 덧셈도 마찬가지이다. 소수점 자리를 맞춰야한다. 두 수의 지수부에서 지수부가 작은 쪽이 지수부가 큰 쪽에 맞춘다.

위 예제에서는 오른쪽 수의 지수부가 왼쪽 수의 지수부보다 작으므로 오른쪽 지수부의 수를 높이고 소수부를 낮추는 것을 확인할 수 있다. 그 뒤로는간단하게 소수부끼리 덧셈을 진행하고 마지막에 Normalization을 하면은 완료된다.

adder hardware

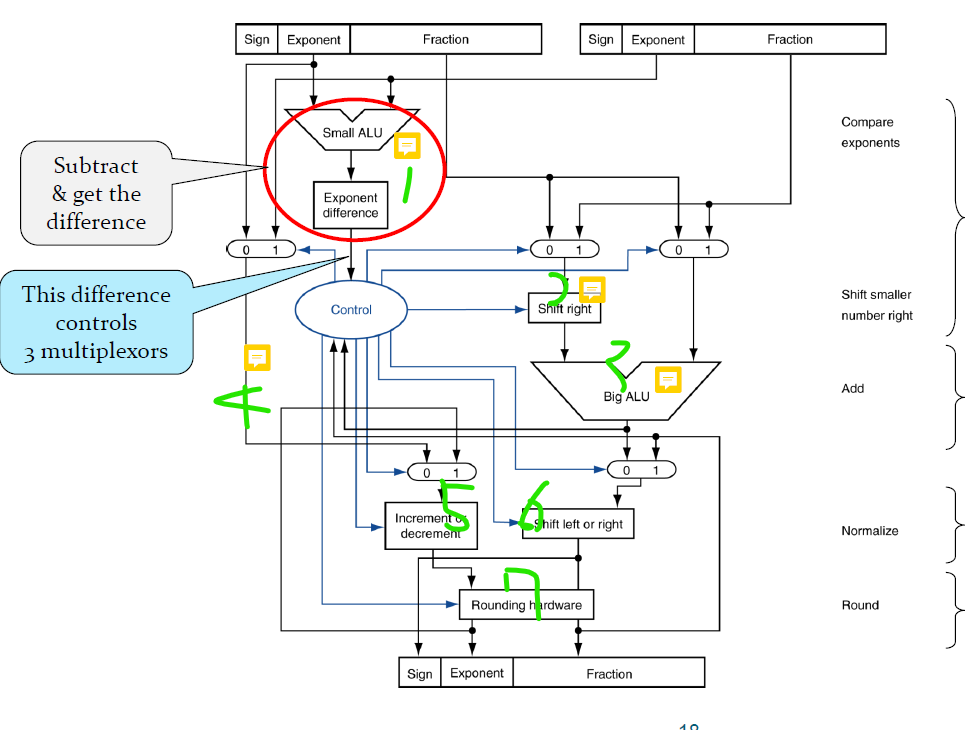
부동 소수 덧셈기의 하드웨어 아키텍처는 위와 같다. 연두색으로 표시된 수를 봐보자.

1. Exponent의 값들을 계산하는 Small ALU가 있다. 그 다음 두 수중 어떤 수의 Exponent가 큰 지를 확인해서 계산한다.
2. Shift right는 LSB연산을 하는 것을 의미한다. Exponent가 작은 쪽이 큰 쪽에게 맞춰야하기 때문에 지수부는 커지고 소수부는 작아져야한다. 소수부가 작아지려면 소수부에 LSB연산을 해주어야 한다.
3. 두 수의 Fraction을 계산하는 ALU이다. Fraction은 Single precision에서는 23비트, double precision에서는 52비트의 연산을 수행할 수 있다.
4. 연산의 결과의 Exponent는 두 수의 exponent 중에 큰 쪽에 맞추기 떄문에 큰 수의 exponent를 흘려보내주는 부분이ㅏㄷ.
5. 5번과 6번은 Normalization을 위한 부분이다. 5번은 소수부의 값을 더하거나 빼는 역할을 한다.
6. 소수점을 맞추기 위해서 shift 연산을 수행한다.

Multiplication

부동 소수의 곱셈은 덧셈보다 쉽다. 소수부끼리 곱하고 지수부끼리 더해주면 된다. 하지만 유의할 점은 있다. 지수부를 실제 Exponent에 적을 때는 bias를 빼서 넣어주기 떄문에 bias를 다시 더해서 원복 후에 더하고 다시 bias를 빼서 Exponent에 적어주면 된다.

FP register & instruction

기존에는 x0, x1 등 x가 prefix로 붙은 레지스터를 사용했다. 하지만 정수와 소수는 포멧이 다르므로 FP에서는 다른 레지스터를 사용한다.
Single presicion은 S가 prefix로 붙은, Double precision은 D가 prefix로 붙은 레지스터를 이용하며 실제로 S는 D의 오른쪽 32비트를 이용하는 것이다.

각 부동 소수를 불러오기 위한 명령어들도 밑에 기술되어있다.

Accurate Arithmetic

우리가 소수부를 더하거나 뺄 때 실제로 모든 비트를 다 계산하지 못할 수도 있다. 왜냐면 single precision을 기준으로 fraction은 23비트인데 소수점을 맞추기 위해서 특정 수의 fraciton이 23비트에서 몇 자리가 잘려서 21비트만 사용이 가능한 경우도 있기 때문이다. 이럴 경우를 대비해서 guard , round, sticky라는 추가 비트를 이용해서 반올림 하여 보다 정확한 연산을 수행할 수 있게 도와준다.

이런 추가적인 하드웨어를 통해서 연산을 더 정확하게 할 수도 있다. 하지만 그에 비례한 cost가 추가적으로 들기 때문에 적당히 타협을 봐야한다.

Subword parallelism

128비트 adder는 128비트의 수 2개를 덧셈하기 위해서 만들어졌다. 하지만 이를 이용해서 32비트 덧셈을 동시에 4번을 수행할 수도 있다. 이것을 두고 Subword parallelism 이라고 한다.

명령어 하나도 여거 개의 연산을 수행하는 것을 SIMD라고 하며 GPU에 적용되어 있다. CPU에는 AVX라고 하여 벡터를 이용해서 여러 개의 연산을 한 번에 수행할 수 있는 기능을 제공한다.

V는 128비트 레지스터이다.
위와 같이 V레지스터를 이용해서 1Byte 단위의 연산 16번을 동시에 실행할 수도 있고 32비트 단위의 연산을 4번을 동시에 할 수도 있다. 밑의 연산에 FADD를 통해서 FP add임을 알 수 있다.