Learning the Structure of Generative Models without Labeled Data 정리

개요

• 통계적 의존성은 Weak supervision 에서 자연스럽게 발생함
• 그러나 사용자가 직접 상관성을 고려해 라벨함수를 작성하거나 좀 더 정확한 휴리스틱으로 다른 사용자를 강화하기 위해 의도적으로 설계된 라벨 함수를 작성하는 것은 문제
• 아래의 세 가지 이유로 사용자가 직접 종속성을 지정하는 것은 실용적이지 못함
  1. 비전문가가 이러한 종속성을 지정하기 어려움
  2. 한 라벨 함수에서 많은 라벨을 태깅 하기 위해 조건을 완화하면 종속성 구조가 빠르게 변경될 수 있음
  3. 종속성 구조가 데이터 세트에 따라 다를 수 있음
• 따라서. Data Programming 논문에서의 결합확률 분포의 종속성 구조를 자동적으로 찾아주는 알고리즘

종속성 고려 알고리즘 제안

• 조건부 독립 모델은 각 $x_i, y_i$에 대한 여러 라벨 함수 출력을 연결하는 고차 요소를 포함하여 추가 종속성이 있는 factor graph 로 일반화 하겠다.

• 제시한 일반 모델의 형태는 아래와 같음

  • $P_{\theta}(\Lambda, Y) \propto exp(\sum_i^m\sum_{t\in T}\sum_{s\in S_t}\theta_s^t\phi_s^t(\Lambda_i, y_i))$

  • $T$: 관심 있는 종속성 유형의 집합 = {표준 종속성, 결합 종속성}

  • $S_t:t\in T$ 유형의 각 종속성 유형에 참여하는 label functions의 index number 집합

  • 종속성 정의

    • 1.표준 상관 종속성

      

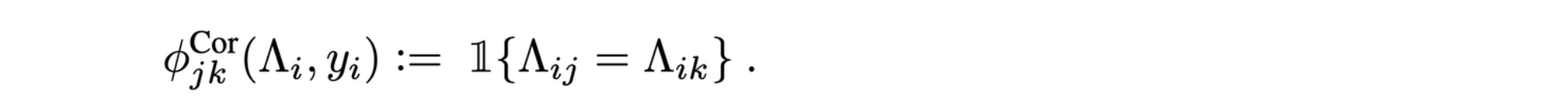
    • 2.결합 종속성

      더 많은 변수를 포함하는 고차 종속성 고려

      

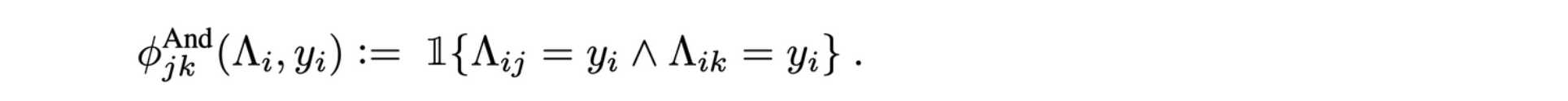
  • $P_{\theta}(\Lambda, Y)$의 구조를 추정하는 것은 Y가 latent value 이므로 어려움(train 중에도 관측 값으로 사용하지 않으므로 → 즉, ground truth가 없는 상태로 학습한다는 것)

  • 따라서 marginal likelihood $P_{\theta}(\Lambda)$을 구함, 또한 생성 모델의 매개 변수를 공동으로 학습하기 위해 Gibbs 샘플링 이용 → 결합 분포는 복잡하지만 완전 조건부 분포(Full conditional posterior distribution)를 구하기 쉬운 형태로 주어지는 경우 Gibbs 샘플링을 적용하기 용이

  • Gibbs 샘플링에 대한 간단한 설명

    • 즉, 사후 분포는 $P_{\theta}(Y)$인데 깁스샘플링을 통해 사후분포에서 생성 됐을만한 샘플을 만들 수 있음.
    • 샘플 생성은 주어진 데이터로부터 완전 조건부 분포를 통해 할 수 있다.
    • 예를 들어, 라벨 함수가 3개 이면 모수가 세 개 있을 것 $( \theta_1, \theta_2, \theta_3)$이고 아래의 결합 확률 분포로 나타낼 수 있음
    • $P(\theta_1,\theta_2,\theta_3,y) = P(y\ |\ \theta_1,\theta_2,\theta_3)P(\theta_1,\theta_2,\theta_3)$
    • 위 결합확률 분포로 부터 full conditional distribution을 찾는다.
    • $P(\theta_1 | \theta_2,\theta_3,y)$
    • $P(\theta_2 | \theta_1,\theta_3,y)$
    • $P(\theta_3 | \theta_1,\theta_2,y)$
    • 아래의 $t$를 10,000번 반복하면
      • $\theta_1^{\ t+1}$ ~ $P(\theta_1 | \theta_2^t,\theta_3^t,y)$
      • $\theta_2^{\ t+1}$ ~ $P(\theta_2 | \theta_1^{t+1},\theta_3^t,y)$
      • $\theta_3^{\ t+1}$ ~ $P(\theta_3 | \theta_1^{t+1},\theta_2^{t+1},y)$
    • 따라서 최종적으로 아래의 샘플을 얻는다.
    • $\{\theta_1^t,\theta_2^t,\theta_3^t\}_{t=1}^{10000}$ ~ $P(\theta_1,\theta_2,\theta_3 |\ y)$

  • 목표 함수 최적화 문제를 pseudolikelihood 형태로 나타내면 아래의 식을 최소화 하는 $\theta$를 찾는 문제로 변환

    • pseudolikelihood 정의

      • $given \ random \ variables \ X = x=(x_1,x_2,\cdot \cdot \cdot ,x_n)$
      • $logL(\theta) = \sum log P_\theta(x_i | x_j \ for \ j \ne i ) = \sum_i P_\theta(x_i|x_{-i})$
      • likelihood의 근사치를 구해 효율적 계산을 하고자 할 때 사용

    • pseudolikelihood 식에 $l_1$정규화 항 추가

    • $argmin_{\theta} \ -logP_{\theta}(\bar\Lambda_j \ | \ \bar\Lambda_{\setminus j }) \ + \epsilon||\theta||_1$

    • 위 식을 아래와 같이 전개하면

    • $argmin_{\theta} \ -\sum_{i=1}^m log \sum_{y_i} P_{\theta}(\bar\Lambda_{i,j},y_i \ | \ \bar\Lambda_{i\setminus j }) \ + \epsilon||\theta||_1$ $\quad \quad \quad \quad , \ where \ \ \epsilon \ \ is \ a \ hyperparameter.$

  • 위의 각 $log\sum_{y_i}P_{\theta}(\bar\Lambda_{i,j},y_i \ | \ \bar\Lambda_{i\setminus j })$ 항 에 대하여 아래의 기울기 계산 가능

    ${\partial log\sum_{y_i}P_{\theta}(\bar\Lambda_{i,j},y_i \ | \ \bar\Lambda_{i\setminus j }) \over \partial \theta_s^t } = \alpha - \beta$

    $where \ \ \alpha : = \sum_{i=1}^m\sum_{\Lambda_{i,j},\ y_i} P_{\theta}(\Lambda_{i,j},y_i \ | \ \bar\Lambda_{i\setminus j }) \ \phi_s^t((\Lambda_{i,j},\ \bar\Lambda_{i\setminus j } ),\ y_i)$

    , $\beta := \sum_i^m\sum_{y_i} P(y_i | \bar \Lambda_i) \ \phi_s^t(\bar \Lambda_i, y_i)$

  • 각 라벨 함수 $\lambda_j$에 대해 차례로 최적화하여 충분히 큰 매개변수가 있는 종속성을 선택하고 이를 추정된 구조에 추가하는 알고리즘을 수행

• 알고리즘

  • notation
    - Input
    - $\bar \Lambda \in \{-1,0,1\}^{m*n}$ : 관측 값
    - $\epsilon$ : threshold
    - 파라미터 $\theta$를 갖는 확률 분포 $P$, 초기 파라미터는 $\theta^0$
    - $\tau$ : epoch size
    - $\eta$ : step size
    - $K$ : truncation frequency
    - Output
    - $D$ :