RBM 개요
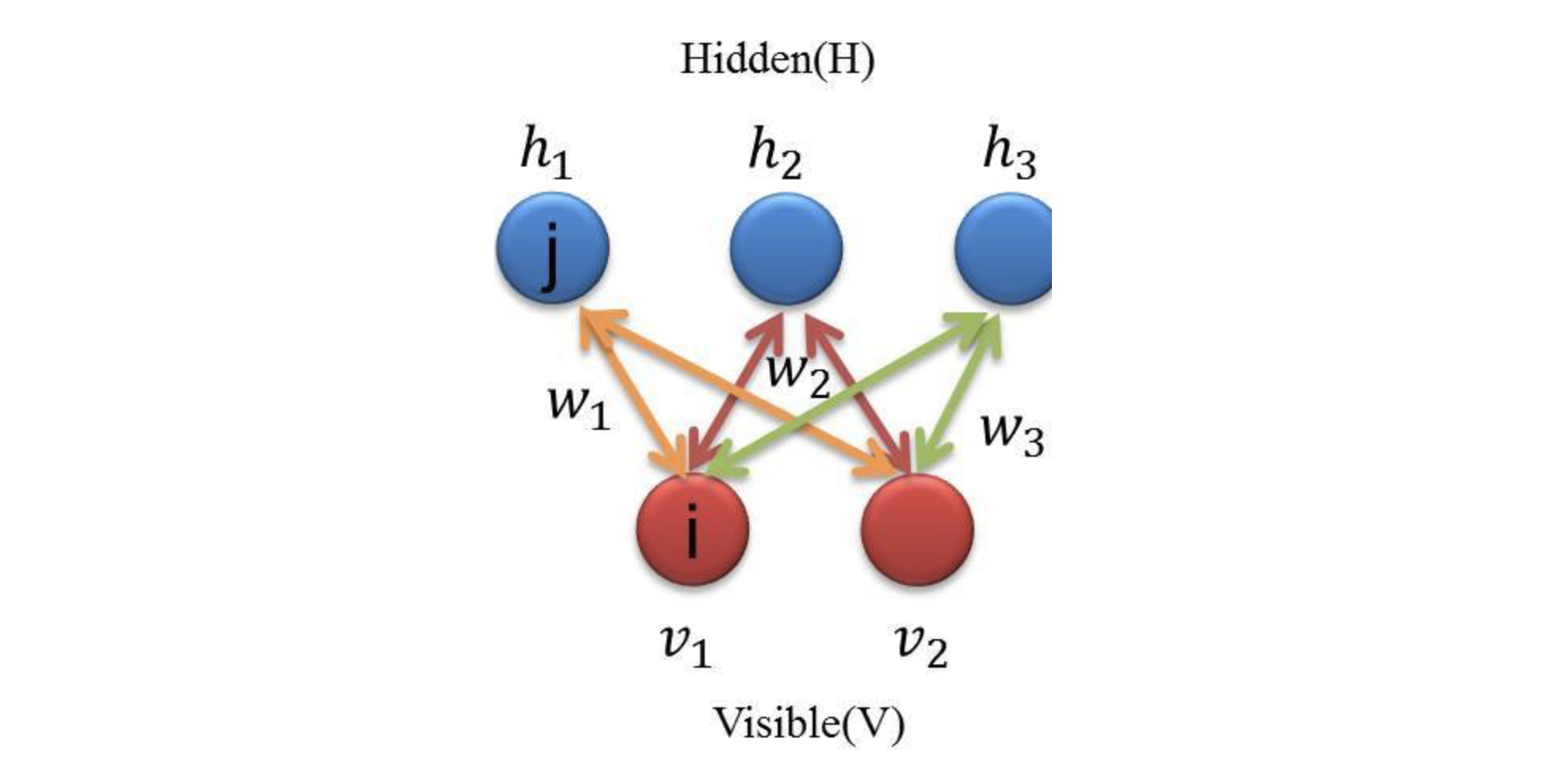
- 같은 노드 사이에는 에지가 없고 가시-은닉 노드 사이에만 에지가 존재하는 무 방향 바이파 타이트 그래프
- 각 노드 마다 weight, bias항 존재
에 속한 특징벡터는 높은 확률로 발생 시키고 아닌 것은 낮은 확률로 발생시키는 알고리즘- RBM은 노드 값에 따라 에너지가 정해지고 에너지가 낮을 수록 발생 확률이 낮음
- 즉, RBM을 잘 학습시키면 원하는 특징 패턴을 높은 확률로 발생시킬 수 있음(원하는 샘플을 높은 확률로 생성할 수 있는 genarative model임)
용어 정의 및 가정
-
학습하고자 하는 매개변수 집합
-
모든 노드 값은 0 혹은 1 값을 가진다 가정(e.g. , 추후 실수 범위로 확장한 논문도 나옴)
-
RBM의 에너지 함수는 아래와 같음
-
행렬 표현으로 나타내면
-
-
위 에너지 식을 이용해 와 가 발생할 확률 계산
- Z는 위의 확률을 다 더하면 1이 되도록 하는 역할
-
의 결합 확률 분포를 이용해 확률 벡터 가 발생할 확률을 아래와 같이 계산
-
즉, 알고리즘을 요약하면 RBM은 내부 상태 의 값에 따라 에너지를 품고, 에너지는 샘플의 발생 확률을 규정. 따라서 어떤 샘플은 자주 발생하지만 다른 샘플은 희소하게 발생하게 할 수 있음(스토캐스틱 생성 모델)
학습 과정
-
목적 함수 정의
-
, 로그의 합으로 표현하는 이유는 언더 플로 방지
→
위의 최적 매개 변수를 찾는 것이 목적이나 최적해 찾는 것이 어려움
따라서 대조 발산 알고리즘을 사용해 근사 해를 구함
-
-
대조 발산 알고리즘
-
-
훈련 집합이 이루는 KL-divergence 값과 모델이 이루는 KL-divergence 값의 차이를 근사 화 하는 것이 대조 발산 알고리즘
-
-
위의 는 RBM의 스토캐스틱 샘플 발생 능력을 활용해 구함, 샘플 발생 과정은 깁스 샘플링을 따름
-
가 입력되었다 가정
-
은닉 노드의 값을 스토캐스틱하게 결정(가 주어졌다는 가정 하)
→
-
아래 식에 따라 를 0 또는 1로 결정(총 개 )
-
3번에서 은닉 노드 값 개를 샘플링 했다면, 반대로 샘플링 된 은닉 노드 값을 이용해 가시 노드 값 샘플링
-
위 한번 루프를 이라 하고 멈춤 조건에 따라 회 반복
- 참고로 식 2, 3번처럼 확률 전개가 가능한 이유는 RBM의 그래프 구조상 같은 종류 노드 끼리는 서로 독립이기 때문
-
-
-
알고리즘 요약
repeat
for (에 속한 샘플 각각에 대해 아래 적용)
식 (ㄱ), (ㄴ)으로 은닉 벡터 를 샘플링
식 (ㄷ), (ㄹ)으로 가시 벡터 를 샘플링
식 (ㄱ), (ㄴ)으로 은닉 벡터 를 샘플링
와 로 를 계산
와 로 를 계산
(b)식을 이용해 를 갱신
until (멈춤 조건)
결론 요약
- RBM의 목적과 사용
- 주어진 데이터 집합에 속한 특징 벡터는 높은 확률로 발생시키고 아닌 것은 낮은 확률로 발생
- 차원 축소, 피쳐 임베딩, 오토 인코더 등으로 활용
- 깁스 샘플링, 대조 발산이 필요한 이유?
- 확률 계산 표본 마다 전부 하게되면 의 수행 시간이 필요(현실적 불가능)
- 따라서 근사 해를 구하는 데 대조 발산 알고리즘을 사용한 것이고 이 과정에서 샘플 발생 전개 방법으로 깁스 샘플링을 사용한 것
- 확률 값의 의미?
- 높은 확률 값은 원하는 샘플 분포를 높은 확률로 발생시킬 수 있다는 것을 의미
- 따라서 확률을 최대화 하는 방향으로 매개변수 학습을 진행하는 것
- 생성 모델이란?
- 벡터 에 대한 확률 분포를 추정하는 비지도 학습을 말함
- 레이블 정보가 있다면 활용하고 무시해도 된다
- 즉, 에 대한 추정
- 반대로 분별 모델은 지도 학습이며 벡터 에 대한 확률 분포에 관심이 없고 단지 예측에 목적을 둠(를 구하는 것)
