BOJ 2143 두 배열의 합 [Java]

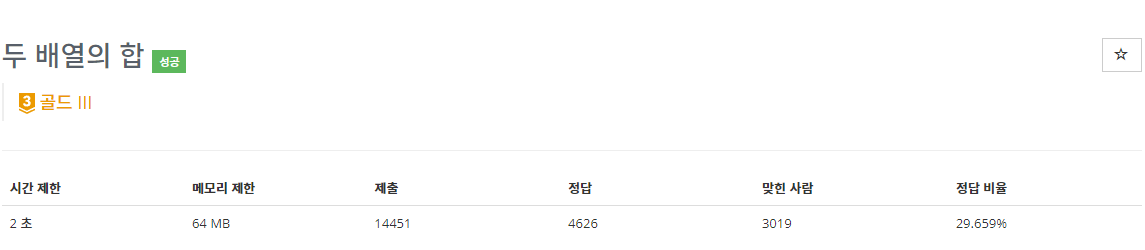
문제

BOJ 2143 두 배열의 합

접근방법

• 부배열과 투포인터 활용
• 전체 부배열을 담는 List가 필요
• 아래는 부배열 생성할 때 직접^~^ 그린 그림이다. 행색이 초라해도 용이하게 쓰였다.
  
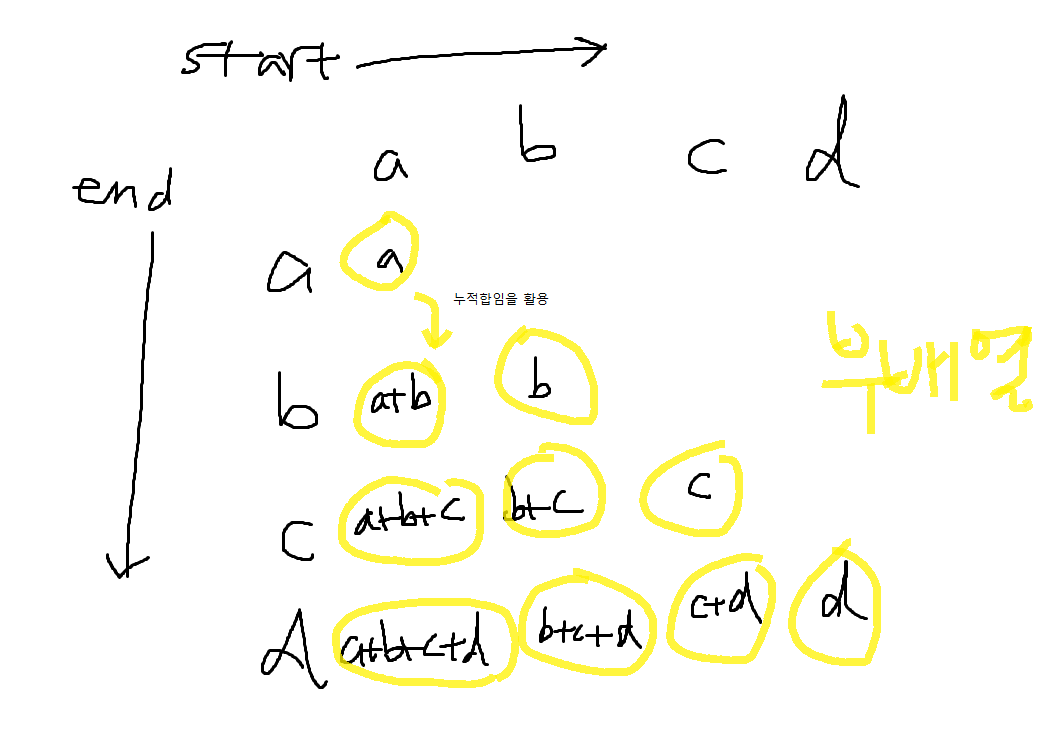
• 시간복잡도를 Big-O 표기법으로 나타내면 사실 부배열 생성 시 O(N^2) 이지만, 이 문제의 쟁점은 그 이외의 시간복잡도를 줄이는 것이다. (대충 아래 그림과 같이 투포인터로)
  
• 위와 같이 안하고 역순으로 정렬하여 같이 올라가는 방법도 있다.
• 출력값이 int의 제곱일 수도 있으니, 적당히 long 자료형을 써야 한다.
• 반복문 들어가기 전에 조건을 잘 따져보자

구현

import java.io.*;
import java.util.*;

// 전체 부배열 경우의 수를 탐색

public class Main {
    static int T, n, m;
    static int[] A, B;
    static List<Integer> subA, subB;


    public static void main (String [] arg) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        T = Integer.parseInt(br.readLine());

        n = Integer.parseInt(br.readLine());
        A = new int[n];
        st = new StringTokenizer(br.readLine(), " ", false);
        for (int i = 0; i < n; i++)
            A[i] = Integer.parseInt(st.nextToken());

        m = Integer.parseInt(br.readLine());
        B = new int[m];
        st = new StringTokenizer(br.readLine(), " ", false);
        for (int i = 0; i < m; i++)
            B[i] = Integer.parseInt(st.nextToken());

        subA = new ArrayList<>();
        int tmpSum = 0;
        for (int i = 0; i < n; i++) {
            tmpSum = 0;
            for (int j = i; j < n; j++) {
                tmpSum += A[j];
                subA.add(tmpSum);
            }
        }

        subB = new ArrayList<>();
        for (int i = 0; i < m; i++) {
            tmpSum = 0;
            for (int j = i; j < m; j++) {
                tmpSum += B[j];
                subB.add(tmpSum);
            }
        }

        subA.sort(null);
        subB.sort(null);
        

        int pa = 0;
        int pb = subB.size()-1;
        long equalCnt = 0;
        while(pa < subA.size() && pb >= 0) {
            int sum = subA.get(pa) + subB.get(pb);
            
            // 만약에 합이 T와 같다면
            if(sum == T) {

                // 동일 개수 확인
                long a = subA.get(pa);
                long b = subB.get(pb);
                long cntA = 0;
                long cntB = 0;

                while (pa < subA.size() && subA.get(pa) == a) {
                    cntA++;
                    pa++;
                }
                while (pb >= 0 && subB.get(pb) == b) {
                    cntB++;
                    pb--;
                }
                
                equalCnt += cntA*cntB;
            }

            else if (sum > T) pb--;

            else if (sum < T) pa++;
        }

        System.out.println(equalCnt + "");
    }
}

제출