[Arxiv 2023] The Capacity and Robustness Trade-off: Revisiting the Channel Independence Strategy for Multivariate Time Series

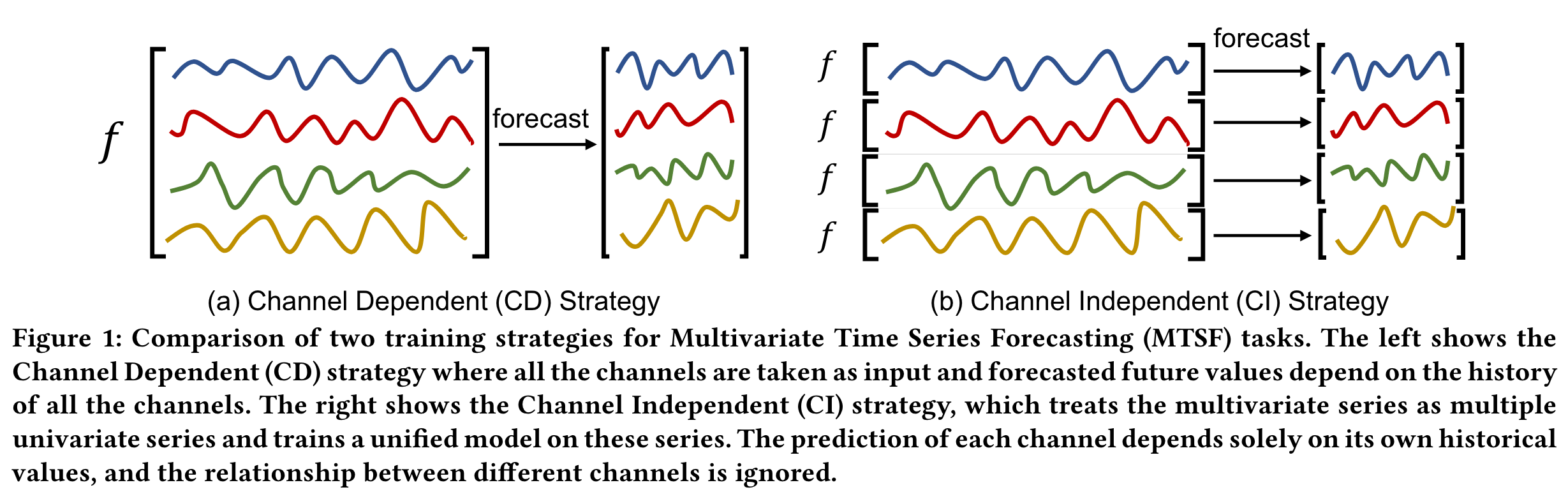
이 논문에서는 Channel Independence strategy에 대해서 이야기하는 만큼 multivariate에 좀 더 집중한다.

multivariate time series의 경우 변수들간의 관계가 예측에 영향을 끼친다.

Channel Independent method : multivariate를 univariate로 보고, correlation을 없앤다? (아마도 무시한다.)

Channel Dependent : Channel Independent method의 정반대로 변수들 사이의 관계를 보는 방법론으로 기존의 방법론들과 유사하다고 보면 좋음.

Channel Independent method는 CD 방법과 비교했을때 아주 우수한 성능을 보여주지만, 그에 대한 이유가 명확하게 밝혀지지 않았고, 이 논문에서는 이를 밝히려고 한다.

이 논문에서는 대부분의 CD방법론이 우수한 성능을 보이지만, distributionally drifted time series의 경우에서는 예외적이라고 한다. 반면에 CI방법론은 robust한 성능을 보여준다. (아마도 이런 약점들을 파고들어서 문제정의를 하면 좋을 것 같다. 또한, 대다수의 논문들에서 distributionally drifted time-series에 대한 예측의 중요성을 이야기한다.)

모델의 설계보다는 CI 훈련 전략이 성능에 큰 영향을 끼치는 것을 알 수 있다. 또, CI stategy의 model capacity가 작지만, robust하고, non-stationary time series에서 잘 적용된다고 한다.

Point

1. 이 논문에서의 훈련전략! (conclusion에서 모델의 설계보다는 훈련 전략이 더 성능에 영향을 끼친다고 했기 떄문에)
2. CD Strategy는 distributionally drifted time series에서 robust하지 않다고 했는데, CI strategy의 무슨 특성이 distributionally drifted time series에 강할까?
3. Channel Independent란?

History

1. LTSF-Linear와 같은 모델들은 기존의 linear 학습과는 다르게 Channel Independent 전략으로 학습한다.이런 학습전략은 global or cross-learning 과 유사하다.
   1. global method : global method는 모든 시계열이 동일한 프로세스에서 나오며, single univariate 예측 함수에 적합하다고 가정한뒤에 학습하는 전략. 이 방법론이 많은 논문에서 우수한 성능을 보여주기도 한다.
2. 이 논문에서는 real-world dataset에서 distribution drift를 보여줌.

훈련전략

훈련전략에는 Channel Independent와 Channel Dependent 두가지가 있는 것.

1. Channel Independent strategy에서 linear model은 모든 변수(channels)에 대한 AutoCorrelation의 평균을 사용한다. 평균을 사용한다는 것은 각각의 모든 AutoCorrelation보다는 덜 drift하기 때문에 성능에 유리한 것 같다. —> model의 parameter(coefficient)가 전체의 ACF에 의해서 결정됨. (CD와 비교하면 CI가 robust할 수 밖에 없다.)
2. Channel Dependent strategy에서는 각각의 AutoCorrelation을 사용한다. —> model의 parameter(coefficient)가 각각으 ACF에 의해 결정됨.

이 둘의 차이는 각 변수마다의 모델이 있느냐 없느냐의 차이. 혹은 각 변수마다 loss function을 정의 하냐 마냐의 차이.

수식 (3)을 보면, $x^{i}_C$의 i는 i번째 변수를 말한다. 즉 loss를 계산할때, 각각의 변수에 대한 예측 결과 loss function을 계산하는 것.

Distribution drift

이 논문에서는 아래의 그림과 같이 train set과 test set에서의 distribution drift를 발견함.

distribution drift를 확인하기 위해서는 train과 test에서의 각각의 ACF를 확인하면 됨.

ACF ? Auto-Correlation Function으로 time lag (시차)에 따른 observation의 correlation이다. 아래의 4.1 Section에서는 ACF에 대한 수식이 있다.