[Arxiv 2022] A comprehensive Survey of Regression Based Loss Functions for Time Series Forecasting

이 논문은 시계열 데이터의 예측, 이상탐지, resource allocation, predictive maintenance 등 다양한 분야에서 사용되는 loss function에 대해서 설명한다. 14가지 정도의 regression loss가 존재하고 이에 따라서 어떤 regression loss가 적합한지를 보여준다.

내가 계속 시계열 연구를 한다고 했을 때, 기존에 사용하던 MSE/MAE 로스 이외에도 다양한 로스를 사용해 볼 수 있다. (이는 좋은 컨트리뷰션이나 포인트가 될 수 도 있다. 대부분의 논문들에서는 mse를 사용하니까..)

시계열 예측과 같이 복잡한 테스크에서 universal한 loss function을 사용한다는 것은 불가능하다. 그렇기 떄문에 데이터 특성에 맞추어서, 혹은 task에 맞추어서 올바른 학습 로스를 사용하는 것이 올바르다.

시계열 데이터는 Level, Cyclicity, Trend, Seasonality, Noise들로 이루어져있다.

Level : 모든 데이터에는 value의 baseline? 혹은 disdtribution이 존재하는데, 예를들어서 National Illness의 ILITOAL 변수의 level은 80000정도 이다.

Cyclicity : 시계열 데이터의 패턴으로 볼 수 있으며, 반복되는?그런걸 말한다. 

Trend : 시계열 데이터의 증감을 나타낸다.

Seasonality : 시간적 특성을 가지고 나타나는 cycle

Noise : level, cyclicity, trend,seasonality를 모두 제외하고 남은 잔차.

Regression Loss Functions : 

1. Mean Absolute Error (MAE) [L1 loss]

   Advantages	Disadvantages
   Computationally cheap.	linear scoring approach를 따른다. (error를 계산할 때, weighted equally when computing the mean.)
   Less sensitive towards outliers	MAE는 미분가능하지않다.

2. Mean Squared Error (MSE) [L2 loss]

   Advantages	Disadvantages
   MSE는 빠르게 gradient의 minima에 도달한다.	2차 방정식이라는 특성이 있어서 back propagation 도중에 loss가 터질 수 있다(갑자기 엄청 커지는 것)
   MSE는 2차 방정식으로 나타내며, 이상치의 경우 모델에 패널티를 줄 수있다.	MSE는 특히나 outlier에 민감하기 때문에, 데이터의 중요한 이상값이 모델에 영향을 미칠 수 있다.

3. Mean Bias Error (MBE) Mean Absolute Error에서 절댓값만 빠진 상태..

Advantages	Disadvantages
bias를 제대로 학습하게 하기위해서는 사용할만..	학습의 traffic pattern을 예측하려고 시도하면서 지속적으로 한방향으로 error가 발생하도록 한다.

4. Relatvie Absolute Error (RAE)

   $RAE = \frac{\sum^N_{i=1}|y_i-\hat{y}_i|}{\sum^N_{i=1}|y_i-\bar{y}_i|}$ , $\bar{y} = \frac{1}{N}\sum^N_{i=1}yi$

   Advantages	Disadvantages
   RAE는 오류가 다른 단위? 스케일로 측정되는 모델을 비교할 수 있다.	예측 결과가 실제값과 유사해질 경우, RAE를 정의할 수 없다.

5. Relative Squared Error (RSE) [RAE의 분모 분자를 제곱함.]

   advantages	disadvantages
   Error의 데이터의 scale과 무관하기 때문에 다양한 scale의 error 측정시에 괜찮다.	RSE는 예측값의 mean, size에 영향을 받지 않는다.

6. Mean Absolute Percentage Error (MAPE)

   $MAPE = \frac{1}{N} \sum^{N}_{i=1}\frac{|y_i-\hat{y}_i|}{y_i} 100\%$

   advantages	disadvantages
   MAPE 손실은 모든 오류를 100의 단일 척도로 표준화해서 계산한다.	MAPE 방정식의 분모는 예측된 결과이기때문에 0으로 계산될 수 도 있다.
   MAPE는 백분율로 표시되기 때문에 데이터의 scale에 상관없다.	학습이 편향될 수 있다. (양수의 에러가 음수의 에러보다 덜 패널티를 받기 때문에)

7. Root Mean Squared Error (RMSE)

   advantages	disadvantages
   RMSE는 모델에 대한 학습 경험적방법으로 작동함. 쉽게 미분가능,많은 최적화 방법론들이 사용함.	RMSE는 선형 함수이기떄문에 최소값 부근에서 기울기가 급격하게 작아진다.
   RMSE는 MSE 보다 적은 오류 패널티를 적용한다.	데이터의 규모에 따라서 RMSE가 결정된다. error scale이 커짐에 따라서 이상값에 대한 민감도가 커진다.

8. Mean Squared Logarithmic Error (MSLE)

   $MSLE= \frac{1}{N}\sum^N_{i=1}(log(y_i+1)-log(\hat{y}_i+1))^2$

   advantages	disadvantages
   error 값이 작던 크던 상관없다.	MSLE는 에러가 작은 경우에만 더 유리하다.

9. Root Mean Squared Logarithmic Error (RMSLE) [MSLE에 루트 씌운 값.]

   advantages	disadvantages
   outlier?에 큰 영향을 받지는 않는다.	RMSLE는 편향된 패널티를 주기 때문에 학습이 제대로 안될 수 도 있다.

10. Normalized Root Mean Squared Error (NRMSE)

    $NRMS E= \frac{\sqrt{\frac{1}{N}\sum^N_{i=1}(y_i - \hat{y}_i)^2}}{\bar{o}}$ , $\bar{o}$ 는 관측값들의 평균

    advantages	disadvantages
    NRMSE는 scale에 의존하지 않아서 다양한 데이터셋에 적용하기 적당하다.	NRMSE는 response variable? 과 관련된 units을 잃는다. (잘 이해가 되지 않는..)

11. Relative Root Mean Squared Error (RRMSE)

    $RRMSE= \sqrt\frac{{\frac{1}{N}\sum^N_{i=1}(y_i - \hat{y}_i)^2}}{\sum^N_{i=1}(\hat{y_i})^2}$

    advantages	disadvantages
    RRMSE는 다양한 측정 기술을 비교하는데 사용 가능함.	RRMSE는 실험 결과의 부정확성이 잘 안보인다.

12. Huber Loss

    Huber loss는 2차 및 선형 scoring algorithm의 이상적인 조합이다.

    MSE, MAE를 조건에 따라서 잘 적용하였다.
    

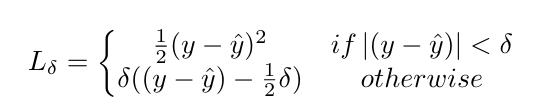
    Advantages	Disadvantages
    선형성은 이상값에 적절한 가중치가 부여된다. (MSE만큼 극단적이지 않음. 델타변수를 추가 함으로써 모든 분포에 유연하게 적응 할 수 있다.)	Huber loss는 추가 조건 및 비교로 인해 계산 비용이 많이 들고, 데이터의 크기가 클 경우 더 많은 비용이 든다.
    델타 아래의 곡선 형태는 back propagation중에 step의 길이가 정확함을 보장한다.	좋은 성능을 위해서는 training의 요구사항이 까다롭다.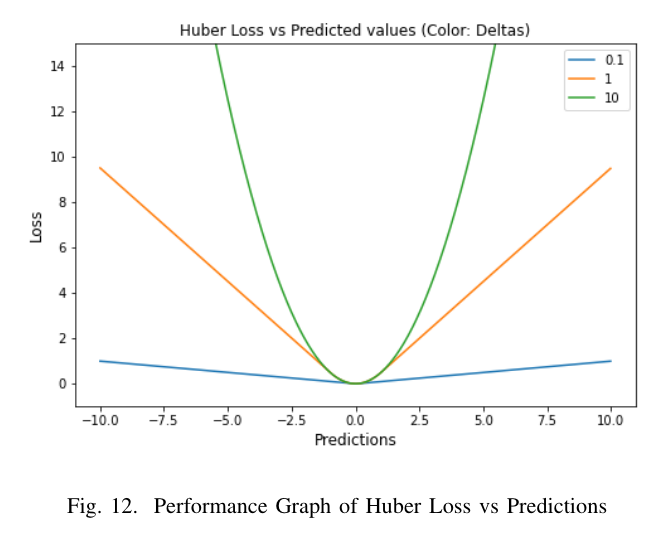

    

13. Log Cosh Loss

    $Logcosh(t) = \sum^N_{i=1}log(cosh(\hat{y_i}-y_i))$

    이 loss에서는 hyperbolic cosine을 계산한다.

    Advantages	Disadvantages
    Log-cosh는 오류의 hyperbolic cosine 로그를 계산한다. 연속성, 미분 가능 등의 측면에서 huber loss보다 이점을 갖는다.	huber loss보다는 유연하게 적용되지는 않는다.
    Huber loss보다 computation이 작다.	아직 연구가 더 필요하다.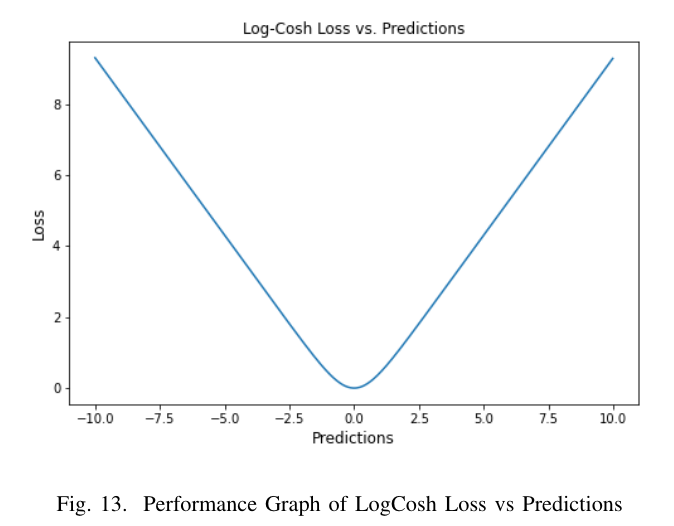

    

[출처 : A comprehensive Survey of Regression Based Loss Functions for Time Series Forecasting]