[AAAI 2021] Informer : Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

Abstract

Long Sequence Time-series Forecasting(LSTF)문제를 Transformer를 기반으로 문제를 해결한다.

Transformer의 단점(quadratic time complexity, high memory usage, inherent limitation of the encoder-decoder architecture)들을 보완한 Informer(proposed method)가 이 논문의 핵심적인 keyword이다.

이 논문에서 제안한 Informer 모델은 LSTF문제를 푸는데 있어서 연산 complexity도 낮추었고, 효과적이며 빠르게 예측을하도록 하는 method를 적용한 모델이다.

어떻게 해결하였고, 얼마나 성능이 개선되었는지 알아보자.

Introduction

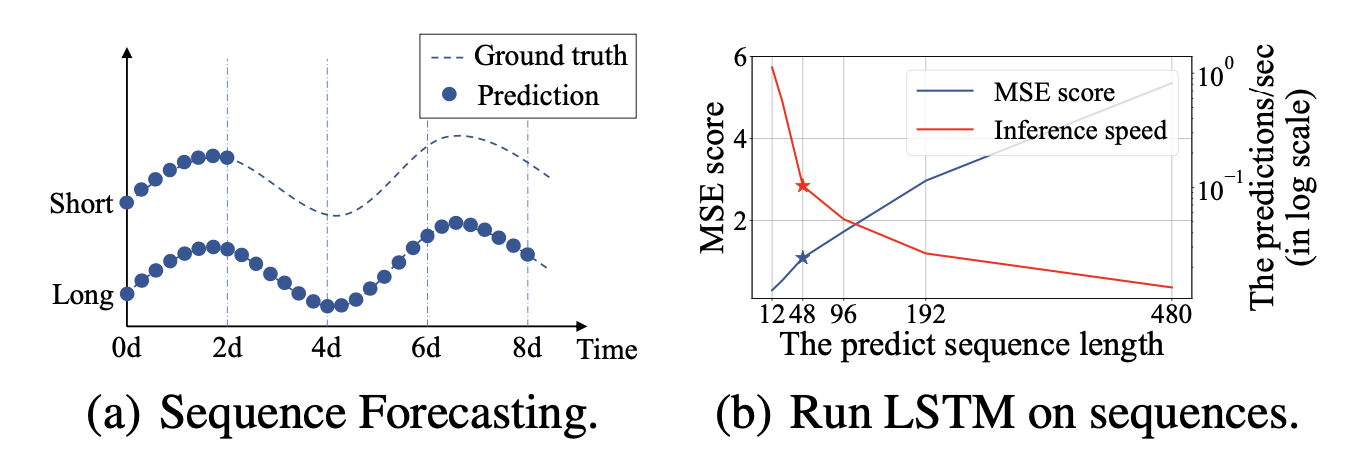
기존의 시계열 예측은 short-term 예측이 주를 이룸.

그림 (a)를 통해 short-term과 long-term forecasting의 차이를 알 수 있다.

그림 (b)에서는 예측해야하는 sequence길이에 따른 mse 를 나타내는데, 예측하는 길이가 길어질수록 mse가 커진다. 여기서 주의깊게 보아야 하는것은 이 논문에서 short-term예측이라고 보는 기준을 48개의 데이터 포인트 를 기준으로잡고있는데, 48개 이상의 sequence예측부터 mse가 급진적으로 증가하는 것을 알 수있고, 또, Inference speed또한 갑자기 낮아지는것을 알 수 있다.

→ 즉, 기존의 모델들이 short-term forecasting만 잘해왔다는 것을 알 수 있다.

The major challenge for LSTF is to enhance the prediction capacity to meet the increasingly long sequence demand, which requires :

(a) extraordinary long-range alignment ability

(b) efficient operations on long sequence inputs and outputs.

Transformer는 RNN메 비해 (a)의 조건을 만족시키지만, (b)조건을 만족시키지 못한다.

1. The quadratic computation of self-attention : attention score 연산 중 dot product 에 의해 메모리와 시간이 $O(L^2)$소요 .
2. The memory bottleneck in stacking layers for long inputs : 1번의 문제점의 quadratic term이 layer 개수에 따라 비례하여 증가.
3. The speed plunge in predicting long outpus : 긴 시퀀스 예측시 시간이 오래 걸림.

기존의 논문들이 1번의 단점을 해결하려 하지만, 이 논문에서 제안하는 Informer에서는 1,2,3을 모두 해결하고자 한다.

Preliminary

LSTF Problem definition

Input $\Chi^t = \{x^t_1,...,x^t_{Lx} | x^t_i \in R^{d_x}\}$

output $Y^t= \{y^t_1,...,t^t_{L_y} | y^t_i\in R^{d_y}\}$

Encoder-decoder architecture

대부분 encoder-decoder 모델 : input representation $X^t$ → Encoder → hidden representation $H^t$ → decoder →output representation $Y^t$

• dynamic decoding : 학습이 끝난 뒤, $\bold{h}^t_k$ 로 $\bold{h}^{t+1}_k$를 생성하고 예측하는 과정.

Input Representation

uniform input representation은 global positional context 와 local temporal context를 잘 반영하도록 해줌. (Appendix B에 이에대한 이야기가 있다.)

RNN models : recurrent 구조로 시계열 패턴을 포착하고 time stamps에 의존하지 않는다.

Vanilla Transformer : point-wise self-attention을 사용하고, time stamps를 local positional context의 역할을 한다

LSTF Problem :

LSTF 문제를 해결하기위해서는 global information(e.g. hierarchical time stamps(ex. week,month,year)나 agnostic time stamps(ex. holidays, events))이 필요하다.

여기서 문제는 global information은 self-attention에서 활용되지 않고, 그렇기 때문에 encoder,decoder사이의 key-query mismatch가 성능저하의 원인이 되기도 한다.

이러한 문제를 해결하기 위해서 이 논문에서는 uniform input representation을 활용한다.

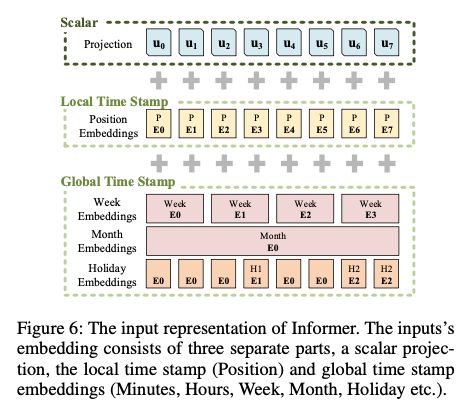
위의 그림에서와 같이 local time stamp 는 positional embedding을 통해서 생성하고,

global time stamp는 learnable stamp embedding을 통해서 만든다.

→ self-attention의 similarity computation이 global context에 엑세스 가능하고, long input에서의 계산이 적당하다는 것.

$\chi^t_{feed[i]} = \alpha u^t_i + PE_{L_x \times (t-1)+i} + \sum_p[SE_{L_x \times (t-1)+i}]_p$

→ $\chi^t_{feed[i]}$ : feeding vector
→ $\alpha$: scalar projection과 local/global time stamp사이의 balance를 조정하는 변수

→ $PE_{L_x \times(t-1) + i }$ : Local time stamp

→ $\sum_p[SE_{L_x \times (t-1)+i}]_p$ : global time stamp

Methodology

time-series forecasting

1. Classical time-series models : 기존의 확률 통계기반의 방법들 ex. ARIMA
2. Deep learning techniques : RNN을 활용한 encoder-decoder기반의 모형들..

Informer는 encoder-decoder구조를 가지고 잇으며 (deep-learning techniques임) LSTF 문제를 푸는것이 목적임.

Efficient Self-attention Mechanism

$\Alpha(Q,K,V) = Softmax(QK^T/ \sqrt d)V$

$A(q_i,K,V) = \sum_j {k(q_i,k_j)\over \sum_l k(q_i,k_l)}v_j$

$k(q_i,k_j)$ 는 kernel smoother로 query와 key의 내적을 근사하는 함수.

1. self-attention을 구하는 과정에서 $O(L_QL_K)$만큼의 메모리 사용량이 생김.
2. self-attention의 확률분포가 sparsity함을 보여왓음. (Sparse Transformer, LogSparse Transformer,Longformer)
   1. 위의 논문들에서 제안하는 Sparse Attention은 heuristic방법론을 따름.
3. 📝 이 논문에서는 Sparse Attention을 생성하는 새로운 접근 방식을 제안함.

   1. Sparse Attention은 (Appendix C에 설명 있음)
      

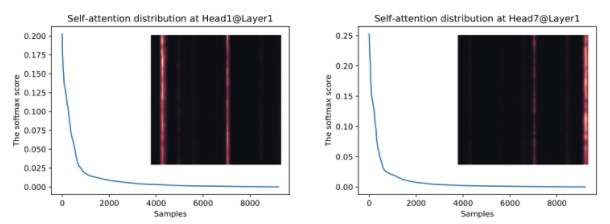
      1. Sparse attention은 위의 그림과 같이 long tail distribution을 갖음.
         1. long tail distribution의 의미 : 소수의 dot-product pairs만이 중요한 어텐션에 기여하고 다른 dot-product pairs는 영향력이 낮은 attention을 생성함을 보여줌.
      2. 이 부분에서 의문점 제시 → 어떤 dot-product가 의미있는지 어떻게 구분할 것인가 ?

Query Sparsity Measurement

dominant dot-product pairs(유의미한 query-key pairs)의 attention 확률 분포가 uniform 분포와 다름.

만약에 $p(k_j | q_i)$가 uniform 분포에 근사한다면, self-attention은 value의 trival sum이 되며, residual input에 중복됨.

그렇기 때문에, $p, q$의 likeness(유사도)가 important query를 구분하는 값으로 사용됨.

이 논문에서는 likeness를 계산하기 위해서 Kullback-Leibler divergence를 사용함.

$KL(q||p) = ln\sum^{L_k}_{l=1} e^{q_ik^T_l/\sqrt d}- {1 \over L_k} \sum ^{L_K}_{j=1}q_ik^T_j/\sqrt d -lnL_K$

위의 수식의 마지막 상수항뺌으로써 I-th query의 sparsity를 측정한다.

$M(q_j,K) = ln\sum^{L_k}_{j=1} e^{q_ik^T_j/\sqrt d}- {1 \over L_k} \sum ^{L_K}_{j=1}q_ik^T_j/\sqrt d$

이 식에서 첫번째 항은 log-sum-exp이고 두번째 항은 arithmetic mean(산술평균)이다.

M이 클 수록 attention probability p는 다양한 확률 값을 갖고, 유의미한 dot-product pairs를 가질 가능성이 높다. 또 위의 long-tail distribution그림의 header부분에 해당하는 pair가 됨.

ProbSparse Self-attention

이 논문에서는 위의 Query Sparsity Measurement 부분에서 정의한 $M$을 바탕으로 의미있는 query에만 집중하는 attention인 “probSparse Self-attention”을 생성한다.

probsparse self-attention은 다음과 같이 정의된다.

$A(Q,K,W) = Softmax({\bar Q K^T \over \sqrt d })V$

$\bar Q$ : sparse matrix (same size of q)

Sparse matrix는 $M$을 바탕으로 top-u의 query들만으로 구성함.( $u = c * lnL_Q$ )

이렇게 되면, query-key lookup에 대해 $O(lnL_Q)$만큼의 query에 대해서 dot-product연산을 수행하고, $O(L_KlnL_Q)$만큼의 layer memory를 사용함.

하지만, 잘 생각해보면, top-u개의 query를 잘 추출하기위해서 결국 $M$연산을 전부 해보아야한다. 즉, $O(L_QL_k)$의 연산이 필수적임.

→ 효율적으로 query asparsity metric인 $M$을 측정할 수 있는 “empirical approximation”을 제안함.

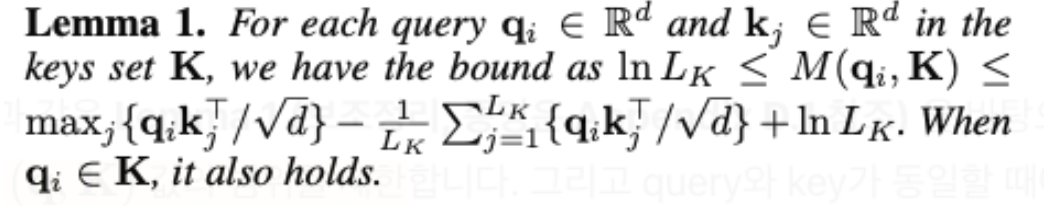
Lemma 1 에서는 query sparsity $M$값의 범위를 조정하였고, 이 식들의 정리를 통해서 max-mean 근사값을 정의함. (효율적으로 연산하기위해서! )

$\bar{M}(q_i,K)=max\{ {q_ik^T_j\over \sqrt d }\} - {1 \over L_k}\sum ^{L_k}_{j=1}{q_ik^T_j\over \sqrt d}$

이 근사치 수식을 잘 보면, Lemma 1에서 $M$의 상한값에서 상수부분인 $lnL_K$를 제외한 부분과 같다.

또, 전체를 다 연사나지 않고, query i에 대해서 비교되는 모든 key j 들 중 일부만 random sampling하여 계산.

수식을 살펴보면,

part 1 : $max\{ {q_ik^T_j\over \sqrt d }\}$ → 이 부분은 query i에 대해서 sampling 된 key j들과의 내적의 최댓값.

part 2 : ${1 \over L_k}\sum ^{L_k}_{j=1}{q_ik^T_j\over \sqrt d}$ → 이 부분은 query i에 대해서 sampling 된 key j들과의 내적의 평균

이 두값의 차를 이용해서 top-u query 에 대해서만 attention을 적용함.

주로, self-attention 연산에서는 input query 와 key의 길이가 같기때문에 ProbSparse Self-attention의 총 time complexity와 space complexity : $O(LlnL)$이다.

Experiments

Conclusion