[Arxiv 2023] Revisiting Long-term Time Series Forecasting : An Investigation on Linear Mapping

기존의 long-term time series forecasting 연구들에서는 다양한 구조들이 temporal dependency를 capture하기 위해서 제안되어왔다. 하지만, 이런 복잡한 구조들보다 간단한 linear layer가 더 우수하다는 것을 보여준다. i) linear mapping이 성능에 큰 영향을 끼친다. ii) RevIN, Channel Independent가 성능에 큰 영향을 준다 iii) linear mapping이 periodic feature를 잘 포착하며, input horizon의 길이에 상관없이 우수한 성능을 보여준다.

Channel Independent? [이 부분에 대해서는 논문을 새롭게 읽을 것]

linear mapping이 특정 구간의 periodic pattern을 affine transform을 학습하는 경향이 있다.

affine transformation : 기하학적 왜곡이나 형태 변형을 보정하는데 주로 사용됨. 즉, 이 논문에서는 linear mapping이 periodic pattern을 보정한다고 생각함.

기존의 transformer-based model들은 다양한 attention방법이나 Non-AutoRegressive (NAR)방식을 통해서 성능을 증명한다.

NAR : 자연어에서 나오는 용어이다. NAR을 이해하기 위해서는 AR 구조를 알아야한다.

AR 구조 : 디코딩시에 이전까지의 토큰 입력이 주어졌을 때, 다음 토큰의 확률 값을 최대화하는 maximum likelihood 학습을 진행함.

NAR 구조 : 이전까지의 토큰 정보를 기반으로 두지 않고 생각함.

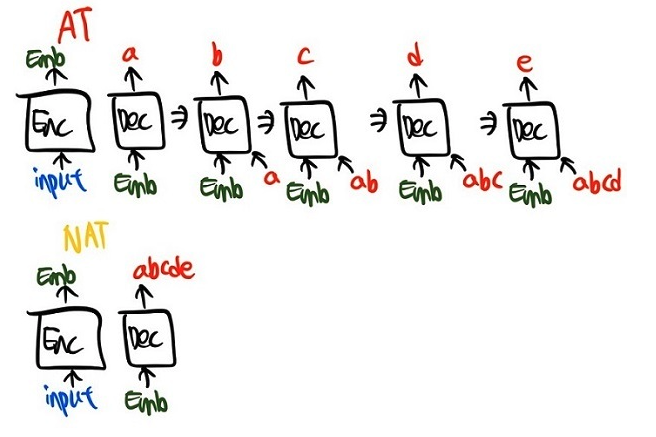
출처 : https://jimmy-ai.tistory.com/311

하지만, LTSF-Linear 모델을 보면, single-linear layer만으로 충분히 우수한 성능을 보여준다. 이 논문에서는 3가지 질문을 중심으로 논문을 전개한다. 1) feature extractor가 정말 효과적인가? 2)linear mapping 의 효율성을 설명하는 기본적인 방법은? 3) linear model들의 한계점은 무엇이고 그걸 어떻게 발전시켰는지.

Linear mapping이 시계열 예측에서 성능에 중요한 영향을 끼침.

Linear mapping이 periodicity를 학습하는데에 있어서 효율적이다.

Linear mapping의 한계점을 찾음.

이 한계점에 좀 더 집중해야한다.

이 논문에서는 심지어 학습되지않은 random feature extractor조차 시계열 예측에서 아주 우수한 성능을 보여준다고 한다. random feature extractor는 뭘 학습할까?

이 그림에서 이야기하고 싶은 것

맨 왼쪽 : Single linear layer한장의 weight

중간 : MLP와 projection layer(linear layer) 각각은 다른 weight를 보여주지만, 결국 마지막 layer에서는 맨 왼쪽과 유사해진다.

맨 오른쪽: Attention이 적용된 뒤에 projection layer를 적용해도 마찬가지로 맨 왼쪽의 weight와 유사해진다.

즉, 어떤 모델이든 linear layer한장과 유사한 결과를 만들어낸다. == 복잡한 모델 사용할 필요없이 간단한 single linear layer면 충분하다!

왜 Linear mapping의 성능이 우수할까?

이 논문에서는 linear mapping이 periodicity를 학습한다고한다. 많은 논문들에서 시계열 분해를 통해서 시계열 데이터를 트랜드, 계절성, 잔차로 나누었지만, 사실 single linear layer를 사용함으로써 그럴 필요가 없어진다. single linear layer가 이미 periodic pattern을 학습하기 때문에!

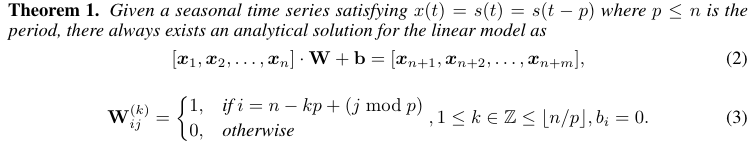
수식 3에서 linear mapping이 periodic signal을 예측할 수 있다는 것을 보여준다.

Section 4.1에서는 single linear layer가 시계열에서 periodicity를 잘 포착한다는 것을 보여준다. 하지만, single linear layer가 trend에서는 우수하지 않은 성능을 보여준다는 것도 실험적으로 보여준다. (수식적인 증명도)

수식 증명도 나중에 쭉 따라가 볼 필요가 있을 것 같다.