06_week_C_malloc_5

9.9.13 명시적 가용 리스트

묵시적 가용 리스트는 할당 시간이 전체 힙 블록의 수에 비례하기 때문에 범용 할당기에는 적합하지 않음 (힙 블록의 수가 사전에 알려져 있고, 작고 특수한 경우에는 더 좋을 수도 있음)

가용 블록 본체는 프로그램에서 필요하지 않기 떄문에 이 자료구조를 구현하는 포인터들은 가용 블록의 본체 내에 저장될 수 있음

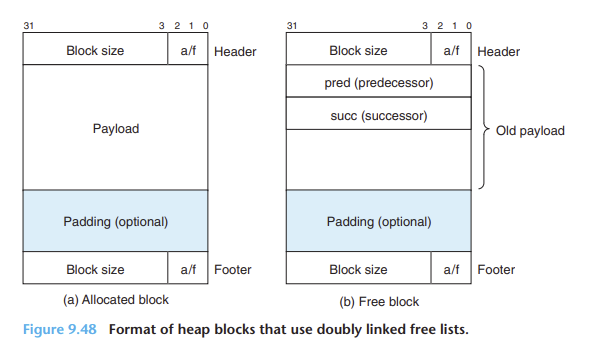
heap에 predecessor와 successor를 가용블록 본체 내에 저장하여 이중 연결리스트로 만들수 있음

묵시적 가용 리스트 대신에 이중 연결리스트를 사용하면 first fit 할당 시간을 전체 블록 수에 비례하는 것에서 가용 블록의 수에 비례하는 것으로 줄일 수 있음
여기에 블록을 정렬하는 정책을 어떤 것을 선택하는가에 따라 비례하거나 상수 시간을 가질 수 있음

1. 후입선출 순을 유지하는 방법
   LIFO 순서와 first fit 배치 정책을 사용하면, 할당기는 대부분 최근에 사용된 블록들을 먼저 조사함 --> 블록의 반환은 상수 시간에 수행--> 경계 태그를 사용하면 연결도 상수 시간에 수행가능

2. 리스트를 주소 순으로 관리하는 방법
   리스트 내 각 블록의 주소가 다음 블록의 주소보다 작다. --> 이 경우, 블록의 반환은 적당한 선행블록을 찾는 데 선형 검색 시간을 필요
   절충 방안 --> 주소 순서를 사용하는 first fit이 LIFO 순서를 사용하는 경우보다 best fit의 이용도에 근접하는 더 좋은 메모리 이용도를 가진다는 것

명시적 리스트의 단점
가용 블록들이 커서 모든 필요한 포인터뿐만 아니라 header, footer까지 포함해야 한다는 점
--> 최소 블록의 크기가 커지고 잠재적인 내부 단편화 가능성이 증가

9.9.14 분리 가용 리스트

단일 연결 가용 블록 리스트를 사용하는 할당기는 한 개의 블록을 할당하는 데 가용 블록의 수에 비례하는 시간이 필요
할당 시간을 줄이는 대표적인 방법 = segregated storage (분리 저장장치)
segregated storage - 각 리스트는 거의 동일한 크기의 블록들을 저장 (모든 가능한 블록 크기를 크기 클래스(Class Size)라고 하는 동일 클래스의 집합들로 분리하는 것)
크기 클래스를 정의하는 방법은 많이 있음

1. 블록 크기를 2의 제곱
   {1}, {2}, {3,4}, {5-8}, ... , {1,025-2,048}, {2,049-4,096}, {4,097 ~ ∞}
2. 크기가 작은 블록들은 자신의 크기 클래스에 할당하고 큰 블록들은 2의 제곱으로 분리
   {1}, {2}, {3}, ... , {1,023}, {1,024}, {1,025-2,048}, {2,049-4,096}, {4,097 ~ ∞}

할당기는 가용 리스트의 배열을 관리하고, 크기 클래스마다 크기가 증가하는 순서로 한 개의 가용 리스트를 가짐
할당기가 크기 n의 블록이 필요하면 적당한 가용 리스트를 검색
크기가 맞는 블록을 찾을수 없다면 다음 리스트를 검색하는 식으로 진행

간단한 예제 두 개
- 간단한 분리 저장장치
가용 리스트는 간간한 분리 저장장치로 동일한 크기의 블록들을 가지며, 각각은 크기 클래스의 가장 큰 원소의 크기를 갖음
ex) 어떤 크기 클래스가 {17~32} 정의되었다면, 이 클래스에 대한 가용 리스트는 전적으로 크기 32의 블록으로 구성

• 리스트가 비어 있지 않다면 첫 번째 블록 전체를 할당
• 가용 블록들은 할당 요청을 만족시키기 위해서 절대로 분할하지 않음
• 리스트가 비어 있다면 할당기는 운영체제로부터 추가적인 고정 크기의 메모리를 요청(대개 여러 개의 페이지 크기로)하고 이를 동일한 크기의 블록을 나누며 블록들을 함께 연결해서 새로운 가용 리스트를 만듦 --> 할당기는 블록을 반환할 때 이 블록을 해당 가용 리스트의 맨 앞에 삽입됨

장점 :
1. 블록을 할당하고 반환하는 것이 모두 빠른 상수 시간 연산
2. 각 메모리 블록 내의 동일한 크기, 분할 불가, 연결 불가 등이 연합해서 블록당 오버헤드가 거의 없음
3. 할당된 한 개의 블록 크기는 그 주소로부터 추정할 수 있음
4. 연결 작업이 없기 때문에 할당된 블록들은 헤더에 할당/가용 태그가 필요 없음
5. 할당된 블록들은 header가 필요 없으며 연결도 없기 때문에 footer도 필요 없음
6. 할당과 반환 연산이 가용 리스트의 시작 부분에서 삽입, 삭제하기 때문에 리스트는 단일 연결만 해도 됨

단점:
1. 내부와 외부 단편화에 취약함
2. 내부 단편화 : 가용 블록들이 분할되지 않기 때문에 발생
3. 외부 단편화 : 일부 참조 패턴은 가용 블록들이 절대로 연결되지 않기 때문에 발생

- 분리 맞춤(segregated-fit)
할당기는 가용 리스트의 배열을 관리
각 가용 리스트는 크기 클래스에 연관되며, 일종의 명시적 또는 묵시적 리스트로 구성
각 리스트는 잠재적으로 서로 다른 크기의 블록들을 포함하고 있으며, 이들의 크기는 해당 크기 클래스에 포함 됨
그리고 다양한 분리 맞춤 할당기들이 존재

블록을 할당하기 위해서 요청된 크기 클래스를 결정하고, 크기가 맞는 블록을 위해 해당 가용 리스트를 first-fit 방식으로 검색
→ 블록을 찾으면 블록을 분할하고, 나머지를 적당한 가용 리스트에 삽입
→ 블록을 찾지 못하면, 다음 크기의 클래스를 위한 가용 리스트를 검색하고 그래도 없으면, 추가적인 힙 메모리를 운영체제에 요청하고, 새 힙 메모리에서 이 블록을 할당하며, 나머지를 적절한 크기의 클래스에 배치

분리 맞춤 방식은 C 표준 라이브러리에서 제공되는 GNU malloc 패키지 같은 수준의 할당기에서 자주 선택 --> 분리 맞춤 방식이 빠르고 메모리 관리가 효율적이기 때문
검색 시간이 줄어드는 이유
--> 검색이 전체 힙이 아니라 힙의 특정 부분에 제한되기 때문
메모리 이용도 개선 이유
--> 단순한 first-fit 검색이 전체 힙을 best-fit 검색하는 것을 단순화 한 것이어서

버디 시스템

• 각 크기 클래스가 2의 제곱인 특수한 경우의 분리 맞춤 방식
• 기본 아이디어는 $2^m$ 개의 워드를 갖는 힙이 주어지면 각 블록의 크기가 $2^k$인 $0<=k <=m$ 분리 가용 리스트를 운영하는 것
• 요청된 블록의 크기들은 인접한 2의 제곱으로 올림
• 본래는 한 개의 $2^m$ 워드 크기의 가용 블록이 존재

ex) 2^k 의 블록을 할당하려면
k<= j <= m 인 크기의 2^j 인 첫 번째 가용 블록을 찾음
1. --> 만일 j=k이면, 할당
2. 재귀적으로 j=k 일 때까지 블록을 절반으로 분할
이와 같은 분항르 수행할 때, 각가의 나머지 절반(버디)은 해당 가용 리스트에 배치됨
크기 2^k의 블록을 반환하려면, free 가용 버디들은 계속해서 연결
할당된 버디를 만나면 중단

핵심 : 블록의 주소와 크기가 주어지면 이 블록의 버디 주소를 계산하는 것은 쉬움

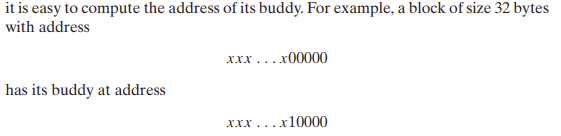
--> 블록과 이 블록의 버디 주소들은 정확히 한 비트 위치만 다름
장점 : 빠른 검색과 연결
단점 : 블록 크기가 2의 제곱이라는 사실은 상당한 내부 단편화를 유발 (특정 application에 국한된 부하에 대해서 블록 크기가 사전에 2의 제곱이라고 알려진 경우, 버디 시스템 할당기는 일정 효과를 거둘 수 있음)