전 게시물에서는 분할 정복에 대해 알아보았다. 이는 계속 배우고 있는 동적 프로그래밍의 한 종류인데, 이번에 배울 동적 프로그래밍은 Matrix-Chain Multiplication이다.
Matrix-Chain Multiplication이란?
해석하는 그대로 행렬들의 곱셈을 의미한다. 행렬들을 곱할 때는 주의 사항이 있는데,
행렬 A와 행렬 B를 곱할 수 있다는 것은, A의 가로 길이와 B의 세로 길이가 동일하다는 뜻이다
가 바로 그 주의사항이다.
m의 너비, l의 높이를 가진 행렬 A와 m의 높이, n의 너비를 가진 행렬 B를 곱하면,
l의 높이, n의 너비를 가진 행렬 C가 나온다.
우리는 단순히 이 2개의 행렬을 곱하는 연산을 하는 것이 아닌, 여러 행렬을 곱셈할 것이다. 이를 나타내주는 것이 Sequence(chain) <A1, A2, ..., An>이다.
Sequence(chain) <A1, A2, ..., An> = A1 A2 ... * An
이다.
예를 들어, chain <A1, A2, A3>가 있고, 각각 10 100, 100 5, 5 * 50의 크기를 가지고 있다고 가정하겠다. 우리는 이를 곱할 때, 2가지 방법을 생각할 수 있다:
((A1 A2) A3) or (A1 (A2 A3))
각각의 시간을 계산해보면
((A1 A2) A3) = 10 100 5 + 10 5 50 = 7500
(A1 (A2 A3)) = 100 5 50 + 10 100 50 = 75000
으로, 첫 번째 방법이 두 번째 방법보다 10배 빠르다는 것을 알 수 있다.
이처럼 배열의 수가 적으면 손으로 계산하는 것도 하나의 방법이겠지만, 배열의 수가 확 늘어나버리면 손으로 계산할 방도가 없어져 버린다. 그러므로, 우리는 여기에도 동적 프로그래밍을 적용할 것이다.
Chain<A1, A2, A3, A4, A5, A6>가 있고, 각각
30 35, 35 15, 15 5, 5 10, 10 20, 20 25
의 크기를 가진다고 가정하겠다.
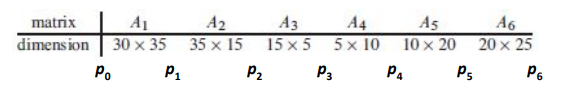
m[i, j] = minimum number of scalar multiplications needed to compute the matrix Aij이고, 점화식은 다음과 같이 나타낼 수 있다.
m[i, j] = 0 (i = j)
min{m[i, k] + m[k + 1, j] + pi-1pkpj} (i < j)
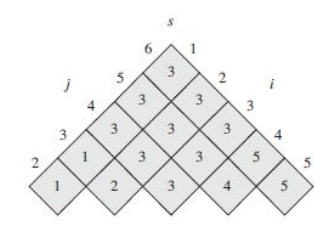
Ai에서의 pi-1은 가로, pi는 세로이다. 위 그림처럼, 사이사이의 값이라고 생각하면 편할 것이다. 이를 모두 이용하여, m에 대한 표와 s에 대한 표를 그릴 것이다.
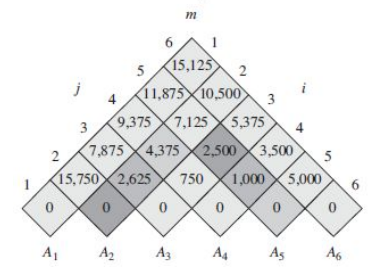
위의 표는 m에 대한 표이다. 위에서 말한 s란, 이 m에 대한 표를 만들 때 최소값이었던 k 값(최적의 k 값)을 적어놓은 표이다. 이에 대한 표도 같이 만들어보겠다.