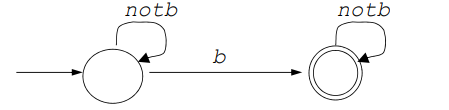전 게시글에서는 컴파일러가 전체적으로 하는 일의 과정, 각 과정에서 무엇을 하는지에 대해 맛보기 식으로 알아보았다. 이번 게시글에서는 토큰, 그리고 이를 정의하는 정규 표현(Regular Expression), DFA(Deterministic Finite Automata), NFA(Nondeterministic Finite Automata)에 대해 알아보겠다.
토큰이란?
소스코드에서 문자열들을 읽어올 때, 이들을 하나의 형태로 만들어야 한다. 이를 토큰이라고 하고, 토큰은 소스코드를 구성하는 가장 작은 구성원이라고 할 수 있다.
토큰은 여러 종류가 있는데,
- 키워드 / 저장된 단어들 : if, while 등등
- special symbols : +, *, >=, <>, ++, ....
- identifier : 문자로 시작하여 문자와 숫자로 구성된 문자열.
- 리터럴(literal) 또는 상수
가 있다.
정규 표현이란?
어떠한 규칙이 만들어내는 문자열의 집합을 표현하는데 사용되는 표현이다. 이를 구성하는 요소에는
- symbol
- alphabet : 상징들의 집합. 실제 알파벳이나 숫자, 한글도 포함될 수 있다.
- meta-symbol : 특정한 의미를 지니는 문자들
이 있다.
정규표현을 표현할 때는
L(r) = r이 만들어 내는 언어(문자열의 집합)
의 모양을 가지게 된다.
문자열 표현에는 null string을 나타내는 ε, 어떤 문자열에도 들어가지 않는 Φ가 있다. ε 표현은 아무런 문자열이 없는게 아닌 null string 하나가 존재한다는 뜻이지만, Φ는 아예 문자열이 없다는 표현이라는 차이점이 있다.
또한, 정규 표현은 선택(Choice), 연결(Concatenation), 반복(Repetition)을 만족한다.
선택 : r | s -> 정규 표현 r과 s 중 하나를 선택
연결 : rs -> 정규 표현 r과 s를 연결
반복 : r* -> 정규표현 r을 0번 이상 반복
우선순위 : 반복 > 연속 > 선택
반복은 0번 이상 반복이라는 것에 유의하자. r이라는 정규 표현이 아예 없는, ε이 나올 수도 있다는 뜻이다.
예를 하나 들어보겠다.
Σ = {a, b, c}에서 정확히 하나의 b만 포함하는 모든 문자열의 집합
= {b}, {ab], {abc}, {acaaccacbaccac}, ...
= (notb)b(notb), notb = (a|c)*
이런 식으로, 일정한 문자열을 만들기 위해 사용하는 표현이 정규 표현인 것이다.
DFA와 NFA란?
이를 알기 위해서는 유한 오토마타(FA, Finite Automata)에 대해 알아야 한다.
FA(Finite Automata)는 각 입력한 문자열에 대해 유한한 개수의 상태 변화가 있는 오토마타를 의미한다. 그 중 DFA는 각각의 입력 문자열 안의 각 심볼에 대하여 유일한 상태변화를 취하는 유한 상태 기계를 의미한다. 의미는 크게 상관이 없으니, 예제로 넘어가겠다.
Σ = {a, b, c}에서 정확히 하나의 b만 포함하는 모든 문자열의 집합
위에서 작성한 정규 표현을 DFA로 표현한 모습이다.
NFA는 DFA와 다르게, 각 입력 문자열 안의 심볼에서 여러 상태변화가 나올 수 있는 FA의 한 종류이다.

위 그림은 정규 표현이 어떻게 코드로 바뀌는지에 대한 다이어그램이다. 우리는 이 과정 중
- RE -> NFA
- NFA -> DFA
를 배울 것이다.
RE -> NFA
Thompson's Construction Algorithm이라는 것을 이용하여, 이 작업을 수행할 것이다.
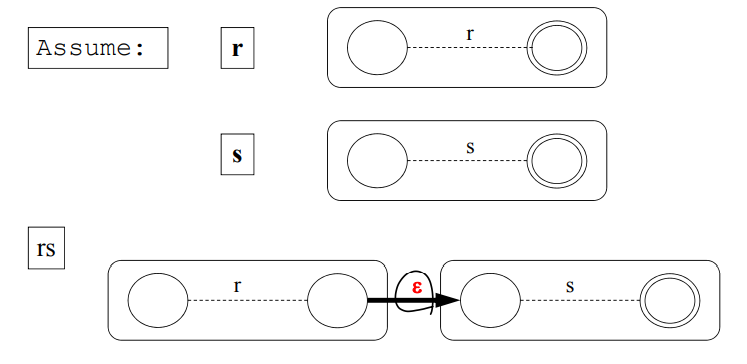
Concatenation(연결)의 표현 방법이다.
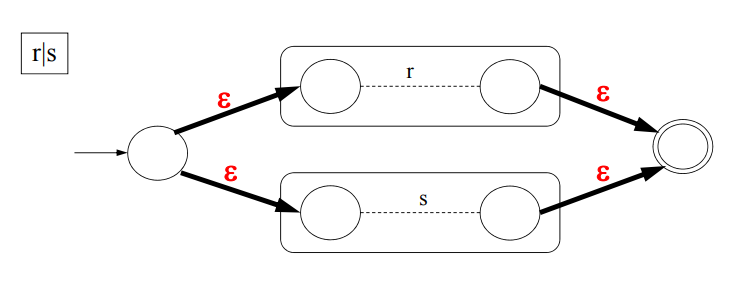
Choice(선택)의 연결 방법이다.
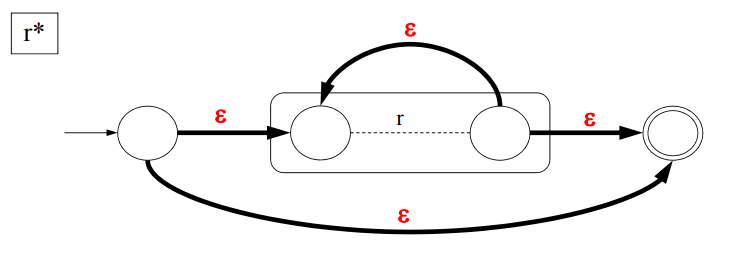
Repetition(반복)의 연결 방법이다.
위의 3가지 연결 방법을 이용하면, 간단하기 정규 표현을 DFA로 변환할 수 있다.
DFA -> NFA
Subset Construction Algorithm이라는 것을 이용하여, 이 작업을 수행할 것이다.
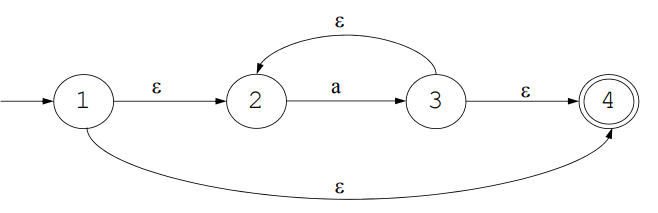
정규 표현 a*
위의 예를 이용하여 간단하게 설명해보겠다.
- 먼저 1(Starting Symbol)에서 ε를 받았을 때, 갈 수 있는 노드들을 조사한다. 이때, 자기 자신도 포함한다. 이를 ε-closure을 구한다고 한다.
ε-closure(1) = {1, 2, 4} - 위에서 구한 노드들의 집합 {1, 2, 4}에서 a를 받았을 때, 갈 수 있는 노드들을 조사한다. 이를 transition이라고 한다.
transition({1, 2, 4}, a) = {3} - 구한 3에서 1번 방법과 같이 ε-closure을 구한다.
ε-closure({3}) = {2, 3, 4} - 구한 {2, 3, 4}에서 2번 방법과 같이 transition을 구한다.
transition({2, 3, 4}, a) = {3}
이 과정을 계속하면 3번, 4번을 반복하게 된다. 반복되는 구간이 나왔으면, ε-closure의 결과들을 하나의 노드로 보고, transition의 결과를 ε-closure한 결과 노드에 연결하면 이런 모양이 나오게 된다:
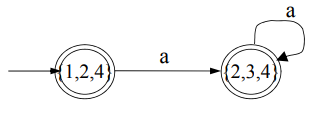
이런 방법으로 DFA를 NFA로 변환할 수 있다.