결측치 제거
summary()로 결측치가 몇개인지 확인할 수도 있다.
is.na( ) : 결측치를 true, false로 나타내는 함수
na.omit() : 결측치 처리하기(but 결측치를 전부 없애기 때문에 결측치 제거과정에서 가장 마지막에 시행해야된다)
정규성 검정
qqnorm(수치형데이터)
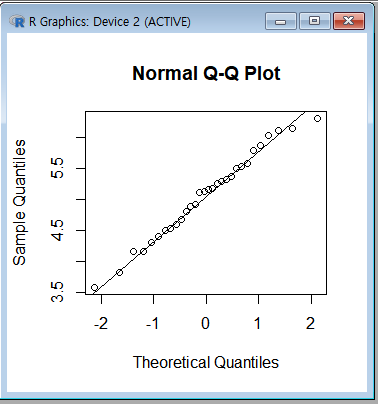
// 데이터의 정규성을 시각적으로 평가하는데 사용
// 정규분포를 따른다면 모든 점들이 45도 대각선을 따라서 직선에 근접하게 배열됨
qqline(수치형데이터) // qq플롯에 45도 대각선 직선을 그린다.
귀무가설 : 변화 X( ~대립가설)
대립가설 : 새로 주장하는 가설
shapiro.test(p$weight) —> p-value 확인
p-value > 0.05 —> 귀무가설 기각 X
제 1종오류 : 옳은 귀무가설을 기각하는 오류
제 2종오류 : 대립가설이 옳은데도 귀무가설을 기각하지 않는 오류
shapiro.test() → 정규성 검정
// 표본크기가 5000이상이면 실행X → 표본 크기가 30 이상이라 중심극한정리에 의해 정규적이다.

-> p-value > 0.05 이기때문에 (H0: 샘플은 정규적이다.)귀무가설을 기각할 수 없다. 따라서 샘플은 정규적이다.
mean-sd table
aggregate(종속변수 ~ 그룹변수, data = 데이터셋, FUN = 함수)
// 그룹별 통계량 계산(범주형 변수를 기준으로 수치형 변수의 통계값을 계산)
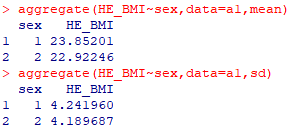
// 성별에 따른 BMI의 mean, sd table
T-검정

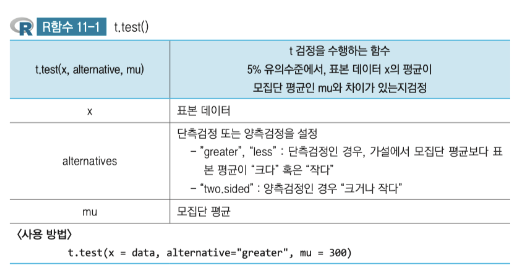


분산검정( var.test() )
분산의 동일성(등분산성) 여부에 따라 t-검정의 방식이 달라질 수 있습니다.
- var.test() 역할 (F-검정)
var.test()는 두 그룹 간의 분산이 동일한지(등분산성)를 비교하는 검정으로, F-검정을 기반으로 합니다.
귀무 가설(H₀): 두 그룹의 분산이 동일하다.
대립 가설(H₁): 두 그룹의 분산이 동일하지 않다.

-> p-value > 0.05 이기 때문에 H0 기각X
남자 그룹과 여자 그룹의 분산이 동일하다.
(Two-sample)t - 검정 : 두 그룹의 평균 비교
t-검정 선택:
분산이 동일할 경우(Student's t-test): t.test(..., var.equal = TRUE)를 사용.
분산이 다를 경우(Welch's t-test): t.test(..., var.equal = FALSE)를 사용.
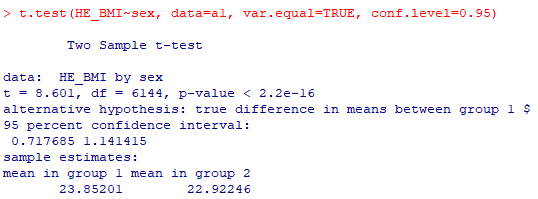
위의 var.test()에서 분산이 동일함을 보였기 때문에 var.equal = TRUE로 검정
p-value < 0.05 이기 때문에 (H0 : 두 그룹의 평균은 같다) 귀무가설을 기각한다.
따라서 t-검정 결과 남자 그룹과 여자 그룹의 BMI평균은 같다고 할 수 없다.
