ANOVA 검정 ->여러 그룹 간의 평균을 한꺼번에 비교할 때 사용한다.

여러개의 t-검정을 시행하는 것 보다 anova검정을 하는 것이 효율적이다.
anova검정은 그룹 간의 분산이 같다는 가정하에 시행됨

따라서 전처리로 그룹간의 분산이 동일한지 확인해주는 bartlett.test()를 먼저 시행!

Bartlett 검정

var.test()는 두 그룹 간의 분산만 비교하지만 bartlett.test()는 두 개 이상의 그룹 간 분산을 비교할 수 있다.

bartlett.test(weight~group,data=p) → 여기서의 H0 : 세 그룹의 분산은 같다.

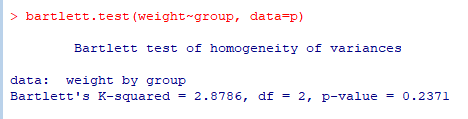
p-value > 0.05 이기에 H0기각X 따라서 세 그룹의 분산은 같다.

이제 그룹간의 분산이 동일한지 확인했으니 ANOVA검정을 한다.

만약 여기서 그룹간의 분산이 동일하지 않다는 결과가 나왔다면?

oneway.test(종속변수~독립변수, data=데이터셋) -> 시행

ANOVA 검정

여러 그룹 간의 평균 차이가 유의미한지 분석한다.
aov(weight~group, data=p)

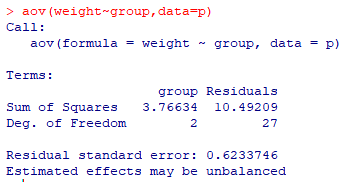
summary를 사용해서 결과를 요약할 수 있다.

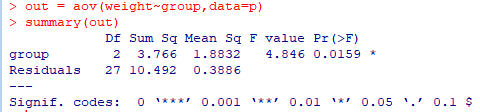
Df: 자유도 (Degrees of Freedom)
Sum Sq: 제곱합 (Sum of Squares)
Mean Sq: 평균제곱 (Mean Squares)
F value: F-통계량 (F-statistic)
Pr(>F): p-value (유의확률)

p-value < 0.05 따라서 (H0 : 그룹 간 유의미한 차이가 없다) 귀무가설을 기각한다.

-> 따라서 그룹 간 유의미한 차이가 있다.

TukeyHSD 사후검정

ANOVA 결과가 유의미하다는 결론이 나면, 어떤 그룹 간에 유의미한 차이가 있는지 구체적으로 알고 싶을 때 Tukey의 사후 검정(Tukey HSD)을 사용

-> 그룹 간의 쌍별 비교를 통해 각 그룹 간 평균 차이가 유의미한지 분석

out = aov(weight~group, data=p)
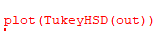
TukeyHSD(out)

diff: 두 그룹 간의 평균 차이.
lwr: 95% 신뢰구간의 하한값.
upr: 95% 신뢰구간의 상한값.
p adj: 조정된 p-value.

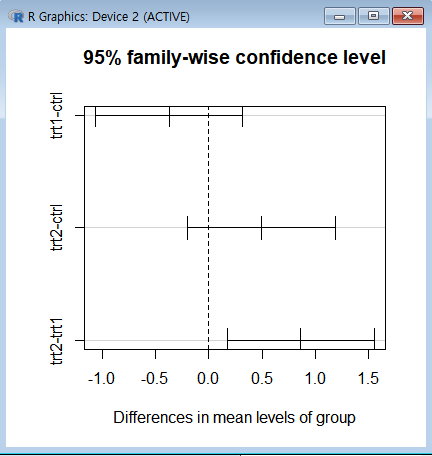
trtl1-ctrl(p-value) = 0.3908 > 0.05 유의미하지 않음
trtl2-ctrl(p-value) = 0.1979 > 0.05 유의미하지 않음
trtl2-trtl1(p-value) = 0.0120 < 0.05 유의미한 차이가 존재

결론:
trtl2-trtl1간의 차이가 유의미함.
다른 그룹 간에는 유의미한 차이가 없다고 볼 수 있음.

분석 절차 요약:

Bartlett 검정 (bartlett.test()): 그룹 간 분산이 동일한지 확인합니다. p-값이 0.05보다 크면 등분산성을 가정할 수 있습니다.

ANOVA 수행 (aov()): 여러 그룹 간의 평균 차이가 유의미한지 검정합니다. p-값이 0.05보다 작으면 그룹 간의 평균 차이가 유의미하다고 결론 내릴 수 있습니다.

Tukey HSD 사후 검정 (TukeyHSD()): ANOVA 결과에서 유의미한 차이가 나타났다면, 어떤 그룹 간의 차이가 있는지 구체적으로 확인합니다.