NumberOfDiscIntersections

🔗 문제 링크

https://app.codility.com/programmers/lessons/6-sorting/number_of_disc_intersections/start/

❔ 문제 설명

We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

A[0] = 1
A[1] = 5
A[2] = 2
A[3] = 1
A[4] = 4
A[5] = 0

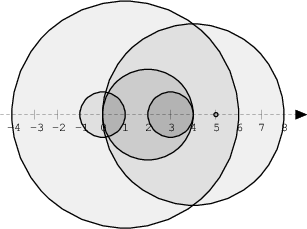
There are eleven (unordered) pairs of discs that intersect, namely:

discs 1 and 4 intersect, and both intersect with all the other discs;
disc 2 also intersects with discs 0 and 3.
Write a function:

def solution(A)

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Given array A shown above, the function should return 11, as explained above.

⚠️ 제한사항

• N is an integer within the range [0..100,000];

• each element of array A is an integer within the range [0..2,147,483,647].

---

💡 풀이 (언어 : Python)

풀이 방법이 전체 탐색외에는 떠오르지 않아 타인의 풀이를 참고했다. 풀이는 꽤 기발한 아이디어다. 한 flow로 교집합의 수를 모두 체킹하는 알고리즘이다. 왼쪽 끝과 오른쪽 끝 좌표를 나누고 이것들을 합친 후에 정렬해서 가장 왼쪽 좌표부터 카운트를 시작해 원의 열고 닫힘을 보면서 겹치는 원의 수를 카운트해주는 아이디어이다.

def solution(A):
    lis = []
    
    for i, a in enumerate(A):
        # -1은 왼쪽 원의 끝, +1은 오른쪽 원의 끝
        lis.append((i-a, -1))
        lis.append((i+a, 1))
    # 가장 왼쪽 기준(음수)에서 시작    
    lis.sort()
    # 교집합 수
    intersect = 0
    # 아직 열려있는 원(카운트 중인)의 수
    opened = 0
    
    for i in range(len(lis)):
        # 원의 오른쪽 끝 좌표만나면 열린 원의 개수 차감
        if lis[i][1] == 1:
            opened -= 1
        # 열린 원의 수만 큼 중첩해서 교집합 수 카운트
        # 원의 왼쪽 끝 좌표만나면 열린 원의 개수 증가
        if lis[i][1] == -1:
            intersect += opened
            opened += 1
    # 천만개 초과시에 -1 반환처리
    if intersect > 10000000:
        return -1
    
    return intersect