★ 트리
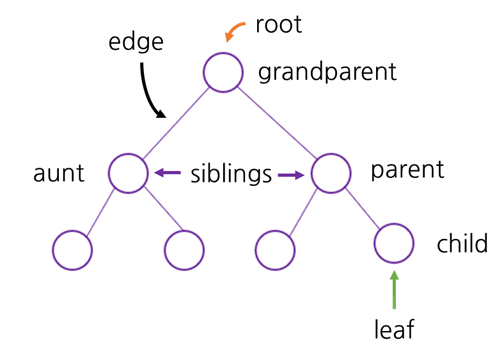
가계도처럼 노드를 나무 형태로 연결한 구조를 트리라고 합니다. 트리에 있는 각각의 요소는 노드입니다. 위 사진에서처럼 노드는 부모, 자식 형태로 이어집니다.
-
뿌리 (root): 트리의 시작 부분입니다. 뿌리를 통해 들어가서 트리를 탐색합니다.
-
잎 (leaf): 자식이 딸려있지 않은 부분입니다.
-
간선 (edge): 두 노드를 연결하는 선입니다. 뿌리로부터의 간선의 수에 따라 level을 나눕니다.
완전 트리와 정 트리
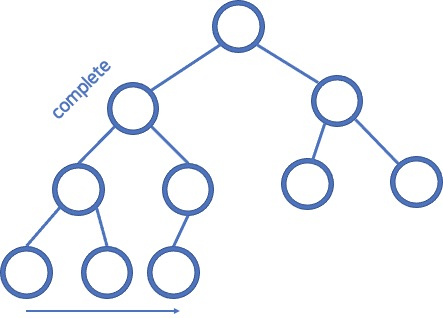
Every non leaf has two children except for the last row & the last row is filled left -> right
완전 트리 (Complete Tree) : 모든 잎이 아닌 노드가 2개의 자식 노드를 가지고 있고 마지막 줄은 왼쪽에서 오른쪽 순서로 채워져 있는 트리입니다.
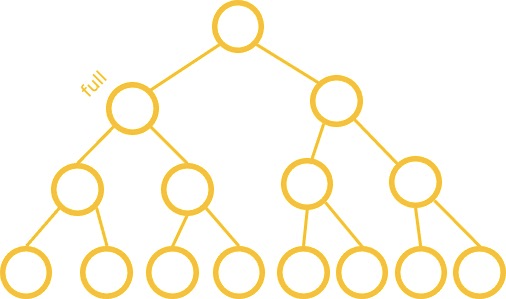
Every non leaf has two children & all the leaves are on the same level
정 트리 (Full Tree) : 모든 잎이 아닌 노드가 2개의 자식 노드를 가지고 있고 모든 잎이 같은 레벨에 있는 트리입니다.
트리 순회 방식
-
전위 순회 (Pre order traversal): 루트 노드에서 시작하여 왼쪽 자식 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법입니다. 다른 모든 노드를 지나기 전에 루트 노드를 방문하기 때문에 이름에 전(Pre)이 들어갑니다.
-
중위 순회 (In order traversal): 왼쪽 자식 노드에서 시작하여 루트 노드에 갔다가 오른쪽 자식 노드로 가는 순회 방법입니다.
-
후위 순회 (Post order traversal): 왼쪽 자식 노드에서 시작하여 오른쪽 자식 노드에 갔다가 루트 노드로 가는 순회 방법입니다.
-
너비 우선 선회/레벨 순서 순회 (Breadth first traversal/level order traversal): 가장 위에 있는 노드에서 시작하여 왼쪽에서 오른쪽으로 가는 순회 방법입니다.
트리 제거 방식
자식 노드의 개수에 따라 트리의 특정 요소를 제거하는 방법은 다음과 같습니다.
1. 잎 노드를 제거할 경우
그 노드의 부모 노드의 포인터를 null로 설정하면 됩니다.
2. 자식 노드가 하나인 노드를 제거할 경우
그 노드의 부모 노드의 포인터를 자식 노드로 향하게 하면 됩니다. 주의할 점은 부모 노드에서 사용했던 포인터와 같은 포인터(left, right 중 하나)를 사용해야 한다는 것입니다.
3. 자식 노드가 2개인 노드를 제거할 경우
중위 후속자와 중위 선임자 중 하나와 자리를 바꾼 후 그 잎 노드를 제거합니다.
중위 후속자(in order successor) : 제거하고자 하는 노드에서 시작하여 왼쪽으로 한 번 내려갔다가 계속 오른쪽으로 내려간 곳의 잎 노드입니다. 중위 후속자는 제거하고자 하는 노드보다 작은 노드들 중에서 가장 큰 노드입니다.
(중위 순회 방식으로 노드를 탐색할 때 루트 노드를 방문하기 직전에 만나게 되는 노드이기 때문에 중위 후속자라고 부릅니다.)중위 선임자(in order predessor) : 제거하고자 하는 노드에서 시작하여 오른쪽으로 한 번 내려갔다가 계속 왼쪽으로 내려간 곳의 잎 노드입니다. 중위 선임자는 제거하고자 하는 노드보다 큰 노드들 중에서 가장 작은 노드입니다.
트리의 회전
균형 잡힌 트리를 만들기 위해 트리의 노드 위치를 바꾸는 과정을 회전이라고 합니다.
연결 리스트처럼 한 방향으로 나열된 트리는 균형 잡혀 있지 않다고 표현합니다. 균형 잡힌 트리에서는 특정 요소를 탐색하는 시간 복잡도가 O(logn)이지만 균형 잡히지 않은 트리에서는 연결 리스트와 같은 O(n)이 됩니다. 따라서, 데이터를 효율적으로 관리하려면 트리를 균형 있게 만들어야 합니다.
조부모 노드, 부모 노드, 자식 노드의 크기 관계에 따라 우측 회전, 혹은 좌측 회전을 합니다. 트리를 재정렬하면 항상 중간 크기의 요소가 가장 위에 있는 루트가 됩니다.
1. 불균형이 왼쪽 서브트리에서 나타날 경우
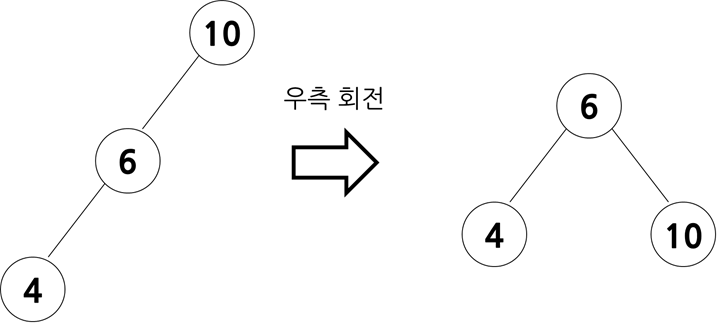
크기 관계는 (조부모 노드) > (부모 노드) > (자식 노드)입니다. 우측 회전을 하여 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮겨줍니다.
2. 불균형이 오른쪽 서브트리에서 나타날 경우
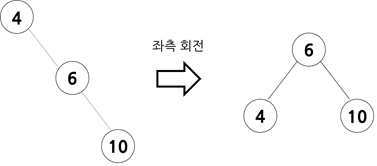
크기 관계는 (조부모 노드) < (부모 노드) < (자식 노드)입니다. 좌측 회전을 하여 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮겨줍니다.
3. 트리가 한 쪽으로 치우치지 않은 경우
- 불균형이 오른쪽 자식의 왼쪽 서브 트리에서 나타날 경우
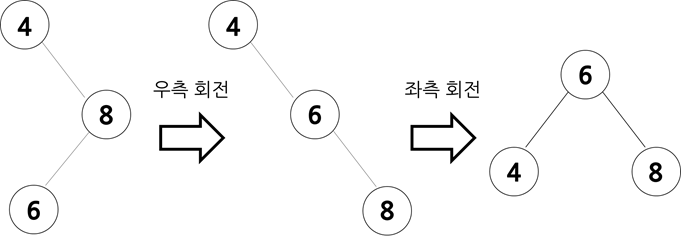
크기 관계는 (부모 노드) > (자식 노드) > (조부모 노드)입니다. 자식 노드에 대해 부모 노드를 우측 회전 후 좌측 회전을 하여 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮겨줍니다.
- 불균형이 왼쪽 자식의 오른쪽 서브 트리에서 나타날 경우
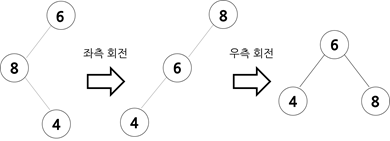
크기 관계는 (부모 노드) > (조부모 노드) > (자식 노드)입니다. 자식 노드에 대해 부모 노드를 좌측 회전 후 우측 회전을 하여 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮겨줍니다.
구현
public class Tree<E> {
class Node<E> {
E data;
Node<E> left, right;
public Node(E obj) {
this.data = obj;
left = right = null;
}
}
private Node<E> root;
private int currentSize = 0;
public void add(E obj, Node<E> node) {
if (((Comparable<E>) obj).compareTo(node.data) > 0) {
// 비교한 수보다 크면 오른쪽으로
if (node.right == null) {
node.right = new Node<E>(obj);
return;
}
add(obj, node.right);
}
// 위에서 오른쪽으로 안갔을 경우, 왼쪽
if (node.left == null) {
node.left = new Node<E>(obj);
return;
}
add(obj, node.left);
}
// 이 메서드를 통해서 위의 메서드를 접근
public void add(E obj) {
if (root == null)
root = new Node<E>(obj);
else
add(obj, root);
currentSize++;
}
// 특정 원소 포함됐는지 여부
public boolean contains(E obj, Node<E> node) {
// 끝에 도달했는데 null이면 없다
if (node == null)
return false;
// node의 data와 일치
if (((Comparable<E>) obj).compareTo(node.data) == 0)
return true;
// 비교해서 오른쪽 혹은 왼쪽 이동
if (((Comparable<E>) obj).compareTo(node.data) > 0)
return contains(obj, node.right);
return contains(obj, node.left);
}
// 좌측 회전: 조부모 노드를 부모 노드의 왼쪽 자식 노드 위치로 옮깁니다.
public Node<E> leftRotate(Node<E> node) {
Node<E> tmp = node.right; // set temp=grandparents right child
node.right = tmp.left; // set grandparents right child=temp left child
tmp.left = node; // set temp left child=grandparent
return tmp; // use temp instead of grandparent
}
// 우측 회전: 조부모 노드를 부모 노드의 오른쪽 자식 노드 위치로 옮깁니다.
public Node<E> rightRotate(Node<E> node) {
Node<E> tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}
// 우측 회전 후 좌측 회전
public Node<E> rightLeftRotate(Node<E> node) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
// 좌측 회전 후 우측 회전
public Node<E> leftRightRotate(Node<E> node) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
}
