힙(Heap)

HeeSeong·2021년 7월 18일

목록 보기

3/4

★ 힙

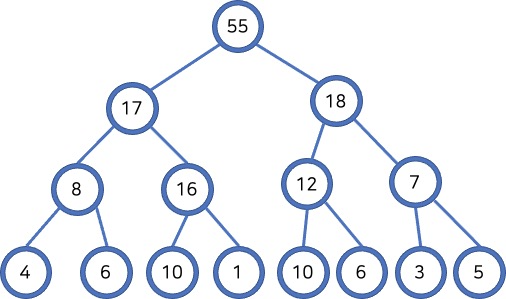
힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기반으로 한 자료구조입니다.

힙에는 최대 힙(max heap)과 최소 힙(min heap)이 있습니다. 부모 노드가 자식 노드보다 크면 최대 힙, 반대이면 최소 힙입니다. 가장 큰 숫자가 뿌리에 있게 하려면 최대 힙, 가장 작은 숫자로부터 시작하려면 최소 힙을 사용하면 됩니다.

종류

parent > children ⇒ MAX HEAP
parent < children ⇒ MIN HEAP

높이 계산

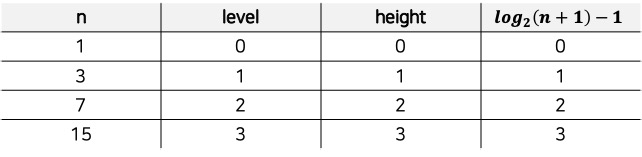
$log_2(n+1) - 1$ 은 height와 일치하므로, 트리에 요소가 몇 개 있는지 알면 트리의 높이를 계산할 수 있습니다.

추가와 제거

힙에 새로운 데이터를 추가하거나 제거할 때 힙의 규칙을 지켜야 합니다. 최대 힙이면 부모 노드가 자식 노드보다 커야 하고 최소 힙은 자식 노드가 부모 노드보다 커야 합니다.

노드 추가

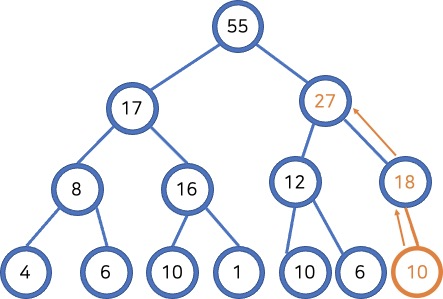
아래쪽에 노드를 추가합니다.
부모 노드보다 큰 숫자인지 확인하고 만약 그렇다면 두 노드를 바꿉니다.

노드 제거

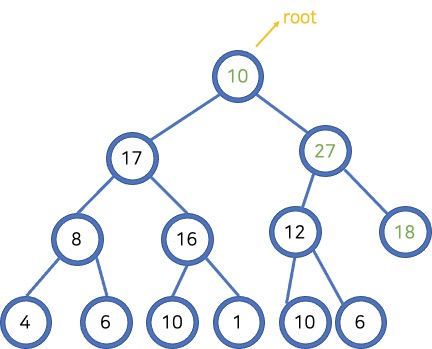
루트를 제거합니다.
트리의 마지막 요소를 루트에 넣어줍니다.
루트에서 시작하여 두 자식 중 큰 노드와 바꿔주어 힙의 규칙을 만족하게 합니다.

무언가를 제거할 때 힙에서는 항상 루트를 제거해야 합니다.

구현

// 힙 배열
E[] array = (E[]) new Object[size];
// 마지막 요소 위치 기록
int lastposition; 
// 힙 원소 추가
public void add(E obj) {
	array[++lastposition] = obj; // 1. 노드 추가
	trickleup(lastposition); // 2. trickle up
}
// 힙 원소 교환
public void swap(int f, int t) {
	E tmp = array[f];
	array[f] = array[t];
	array[t] = tmp;
}
// 힙 자식과 부모 크기 비교해서 정렬
public void trickleup(int position) {
	if (position == 0)
		return;
	int parent = (int) Math.floor((position-1)/2)
	if (((Comparable<E>) array[position]).compareTo(array[parent])>0) {
		swap(position, parent);
		trickleup(parent);
	}
}
// 힙 원소 삭제
public E remove() {
	E tmp = array[0];
    	// 마지막 인덱스를 줄여주어 실제 삭제한 값은 존재하지만 힙의 일부로 생각 안한다.
	swap(0, lastposition--); 
   	trickleDown(0);
	return tmp;
}
public void trickleDown(int parent) {
	int left = 2 * parent + 1;
	int right = 2 * parent + 2;
	// 마지막에 왼쪽 자식이 클 때
	if (left == lastposition && array[parent] < array[left]) {
		swap(parent, left)
		return;
	}
	// 마지막에 오른쪽 자식이 클 때
	if (right == lastposition && array[parent] < array[right]) {
		swap(parent, right)
		return;
	}
	// 마지막에 부모가 클 때
	if (left >= lastposition || right >= lastposition)
		return;
	// 왼쪽 자식이 클 때 혹은 오른쪽 자식이 클 때
	if (array[left] > array[right] && array[parent] < array[left]) {
		swap(parent, left);
		trickleDown(left);
	} else if (array[parent] < array[right]) { 
		swap(parent, right);
		trickleDown(right);
	}
}