문제 링크
문제
티어: 골드 3
알고리즘: 그리디
불면의 밤을 지새워 본 사람이라면 잠 못 드는 그 시간이 얼마나 괴로운지 알고 있다. 잠을 자지 못하는 것은 다음날 피로를 야기하고 삶에 전반적으로 악영향을 미친다. 이러한 이유 때문에 숙면을 신의 축복이라고 부르기도 한다.
하지만 바쁜 현대인들에게 숙면을 취한다는 것은 마냥 쉬운 일이 아니다. 이런 상황을 안타깝게 여긴 인하대학교의 잠마니 박사는 숙면을 취할 수 있는 몇 가지 조건을 제시했다. 아래는 잠마니 박사가 제시한 숙면의 조건 중 일부를 보여준다.
- 침대 주변을 어둡게 한다.
- 자려고 하는 시간보다 일어나는 시간을 조정하려 한다.
..... 이하 생략 .....
극심한 불면증에 시달려 심신이 피폐해진 준형이는 잠마니 박사가 제시한 숙면의 조건을 지켜 잃어버린 정상적인 삶과 건강을 되찾을 수 있게 되었다. 여행을 갈 수 있을 만큼 건강해진 준형이는 기념으로 특별한 여행을 하고 싶었고 인터넷을 통해 특별한 숙소를 예약했다. 하지만 숙소에 도착하고 경악을 금치 못했는데, 그곳에는 정말로 특별한 전구들이 있었기 때문이다.
특별한 전구들은 N개가 일렬로 놓아져 있었고 각각의 전구들은 꺼져있거나 켜져 있었다. 모든 전구를 다 끄고 싶었지만 정말로 특별한 전구들이기 때문에 각각의 전구를 개별적으로 끄거나 켤 수 있는 스위치는 없고 정확하게 연속된 K개의 전구의 상태를 반전시킬 수 있는 버튼만이 있었다. (상태를 반전시킨다는 것은 꺼져있는 전구는 켜지고 켜져있는 전구는 꺼지는 것을 의미한다.)
최대한 빨리 잠이 들고 싶었던 준형이는 최소한의 버튼 조작으로 모든 전구를 다 끄고 싶었지만 최소한은 고사하고 모든 전구를 끄는 것조차 번번이 실패를 하였다. 이대로라면 숙면의 첫 번째 조건을 만족하지 못해 다시 불면증에 빠질 것은 자명한일!! 준형이를 도와 최소한의 버튼 조작으로 모든 전구를 끌 수 있는 프로그램을 작성하자.
아래는 N = 6이고 K = 3일 때 세 번의 버튼 조작으로 모든 전구를 끄는 과정을 보여준다. 세 번의 버튼 조작은 최소한의 조작 횟수이며 이보다 더 적게 조작을 해서 전구를 모두 끄는 방법은 존재하지 않는다.

입력
입력의 첫 줄에는 특별한 전구의 개수 N(1 ≤ N ≤ 100,000)과 한 번의 버튼 조작으로 상태를 반전시킬 수 있는 전구의 개수 K(1 ≤ K ≤ N)가 주어진다.
다음 줄에는 N개의 Si가 공백을 기준으로 주어진다. Si는 i(1 ≤ i ≤ N)번째 전구의 상태를 나타내며 1은 전구가 켜져 있는 것을, 0은 전구가 꺼져있는 것을 의미한다.
출력
모든 전구를 끌 수 있는 최소한의 버튼의 조작 횟수를 출력한다. 한 번의 조작은 정확히 연속된 K개 전구의 상태를 반전시킬 수 있음에 유의한다. 만약 어떠한 조작으로도 모든 전구를 끄는 것이 불가능하다면 “Insomnia”(따옴표는 제외)를 출력한다.
풀이
구하고자 하는 것은 최소한의 버튼 조작으로 모든 전구를 껐을 때 그 횟수이다.
최소한의 버튼 조작은 불필요한 조작을 하지 않는 것이다.
그러니까 조작해서 꺼진 전구를 다시 키지만 않으면 이는 최소한의 버튼 조작이라 할 수 있다.
예를 들어
1 0 0 0 0 1이고 K = 3일 때
인덱스 0인 전구는 켜져있기 때문에 꺼야한다. 그러면
0 1 1 0 0 1이 된다.
이때 인덱스 0인 전구는 조작해서 껐기 때문에 다시 건들지만 않으면 된다.
그러니까 연속된 전구를 조작할 때 포함되지 않으면 되는 것이다.
다음 인덱스 1인 전구는 1이기 때문에 꺼야 되는데 이때 인덱스 0을 포함하지 않으면
그 범위는 1 - 2 - 3이 되는 것이다.
정리하자면, 앞에서 부터 순차 탐색으로 i번 전구가 켜있다면 i ~ i + K - 1를 toggle 해주면 된다.
그런데 N은 최대 100,000이고, K도 최대 100,000이다. 그러니까 위 방식으로 풀면 O(N * K)이기 때문에 시간 제한에 걸린다.
그래서 생각한 방식은 toggle을 해주는 것이 아닌 범위로만 표현하는 것이다.
이때 toggle 범위를 업데이트 해줄 때 새로 추가되는 범위도 통일해 주는 것이 핵심이다.
예를 들어
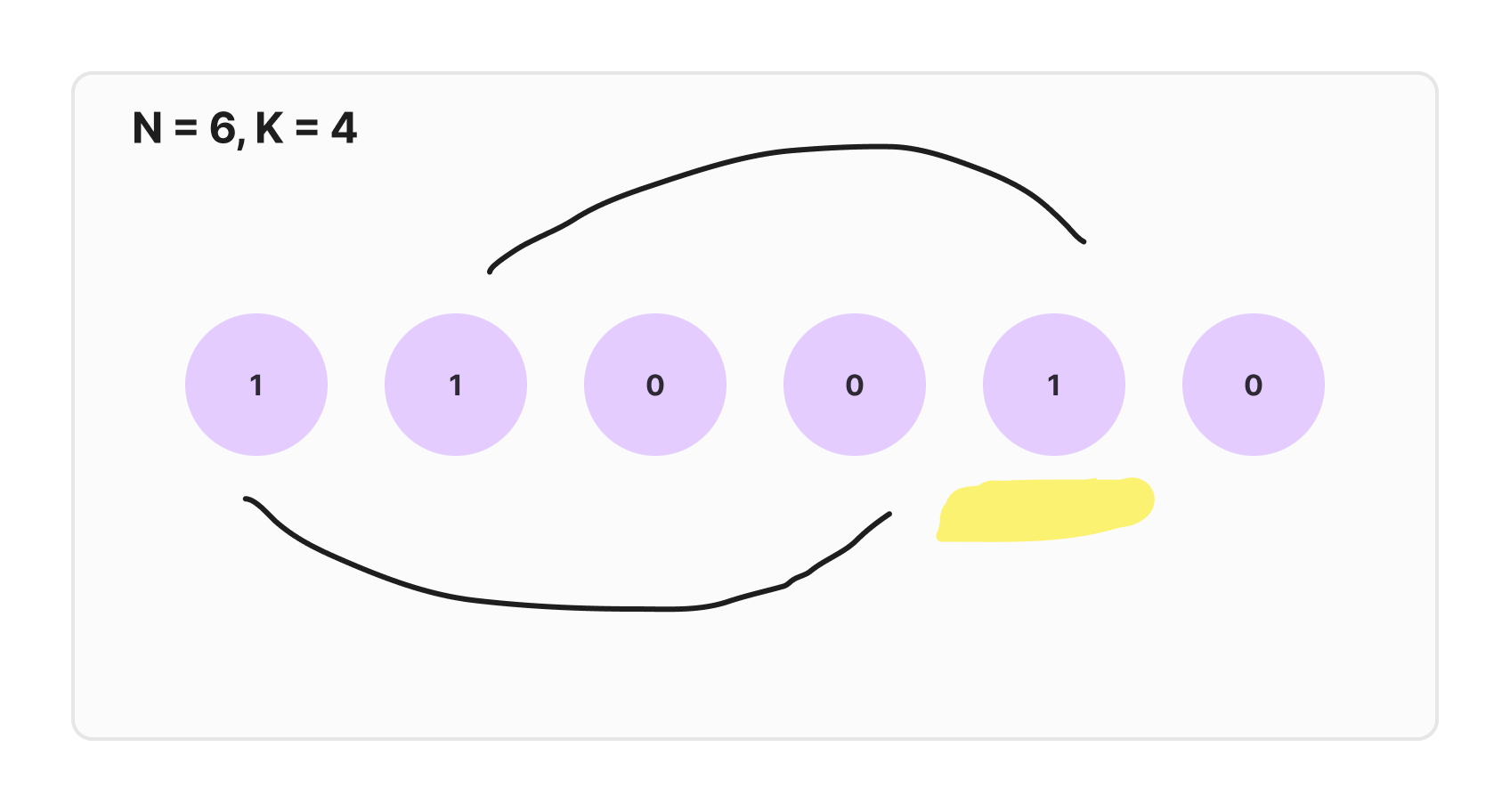
0 번째 인덱스에서 toggle 했다면 X <= 0 + 4 - 1
X 범위에 해당하는 인덱스는 toggle 해줘야 한다.
이때 X 범위에 해당하면서 또 toggle이 발생하면
기존 범위는 결국 toggle == false이고, 새로 추가되는 범위는 toggle == true가 된다.
이때 기존 범위인 <= 3은 toggle false이고, 새로 추가된 범위는 toggle true가 되는데 매번 이런 상황이 발생할 때마다 새로운 범위를 추가해 줄 수는 없다. 그러면 비교 횟수가 늘어나면서 시간 초과가 발생한다.
그러면 새로 추가되는 범위에 toggle을 기존 범위와 맞춰주는 것은 어떨까? 이 생각이 정답이다.
추가되는 범위는 기존 범위 밖이기 때문에 결국 직접 배열의 값을 변환해주는 횟수는 N번을 넘지 못한다.
정리하자면, 1번째 인덱스에서 토글하면 <= 3은 toggle false이고 새로 추가되는 범위인 4번째
인덱스는 toggle true이다. 그래서 4번째 인덱스의 값을 반전 시켜주면 (0 -> 1, 1 -> 0)
toggle false가 되면서, 범위를 업데이트 하면 <= 4는 toggle false가 된다.
이런 방식으로 N - K까지 반복해주고, 마지막 N - K + 1부터 N - 1에 해당하는 인덱스를 toggle과 toggle 범위를 이용해서 정답인지 체크해주면 된다.
시간 복잡도는 O(N + K)다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int N,K;
static int[] bulbs;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
bulbs = new int[N];
StringTokenizer st2 = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
bulbs[i] = Integer.parseInt(st2.nextToken());
}
// int si = 0; //통일된 범위
int ei = K - 1; //통일된 범위
int cnt = 0;
boolean toggle = false;
for(int i=0; i<=(N - K); i++) {
if(i<= ei) {
if(toggle && bulbs[i] == 0) {
//true인 경우에 스위치를 조작하면 기존 범위는 false, 새로 추가되는 범위는 true가됨 그렇기 때문에
//새로 추가되는 범위도 false로 통일해야됨 그래서 그 부분 toggle시키면 false 범위로 통일 가능
cnt += 1;
toggle = false;
for(int j = ei + 1; j <= i + K - 1; j++) {
bulbs[j] = bulbs[j] == 1 ? 0 : 1;
}
ei = i + K - 1; //통일된 범위 업데이트
} else if(!toggle && bulbs[i] == 1) {
//false인 경우 스위치를 누르면 이때는 새로 추가하는 범위도 true로 통일되기 때문에 ei만 업데이트
cnt += 1;
toggle = true;
ei = i + K - 1;
}
} else {
//ei를 벗어나는 경우는 이미 전구가 꺼져있기 때문에 업데이트를 하지 않은거임
if(bulbs[i] == 1) {
cnt += 1;
toggle = true;
ei = i + K - 1;
}
}
}
if(posible(ei, toggle)) {
System.out.println(cnt);
} else {
System.out.println("Insomnia");
}
}
static boolean posible(int ei, boolean toggle) {
for(int i=N-K + 1; i<N; i++) {
if(i <= ei) {
if(toggle && bulbs[i] == 0) {
return false;
} else if(!toggle && bulbs[i] == 1) {
return false;
}
} else {
if(bulbs[i] == 1) {
return false;
}
}
}
return true;
}
}