문제 링크
문제
티어: 골드 2
알고리즘: 그리디, 수학

입력
첫째 줄에 두 정수 x와 y가 주어진다. (0 ≤ x, y ≤ 1012)
출력
윤호가 최소 몇 번 이겨야 하는지 출력한다. 불가능한 경우에는 -1을 출력한다.
풀이
윤호의 점수가 x, 동혁이의 점수가 y가 되는 것이 가능한지 불가능한지 구하고, 가능한 경우 윤호가 최소 몇 번 이겨야 하는지를 구해야 한다.
먼저, 불가능한 경우는 어떤 경우일까?
1 번째 턴은 누군가 1점을 얻는다.
2 번째 턴은 누군가 3점을 얻는다.
3 번째 턴은 누군가 5점을 얻는다.
...
앞 명제를 보면, a1 = 1이고, d = 2인 등차수열임을 알 수 있다.
그러면 x + y는 a1 ~ an까지의 합일 것이고, 여기서 n이 정수가 아니라면 불가능한 경우가 된다.
이 식은 Sn을 구하는 공식이다.
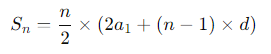
이 공식에 a1과 d를 대입해주면 Sn은 n^2으로 간단하게 변환할 수 있다.
Sn은 x + y이기 때문에 n은 Math.sqrt(x + y)로 간단하게 구할 수 있다.
그런데 n이 정수라고 해서 무조건 가능한 경우는 아니다. 그래서 윤호가 최소 몇 번 이기는지 구하는 과정에서 불가능한 경우를 판별해야 한다.
0에서 x를 만드는 과정에서 포함되는 수를 최소로 하려면, 직감적으로 가능한 큰 값을 포함하는 게 최선이라는 생각이 든다. 그렇지만 증명하기 전까지는 확신해서는 안된다.
결론적으로 가능한 큰 값을 우선적으로 포함하는 것이 최선의 선택이며, 증명 과정은 다음과 같다.
입력이 다음과 같을 때
17 8
n은 5다.
그래서 1 3 5 7 9 중에서 최소한의 요소를 활용해서 17을 만들어야 한다.
여기서 하나 이상의 조합으로 만들 수 있는 10이하의 수는 1 3 4 5 6 7 8 9 10이 된다.
2를 제외하고는 전부 만들 수 있는 것을 알 수 있다.
즉, 17에서 가장 큰 수인 9를 뺐을 때 10이하가 되는데 이 값이 2가 아니라면 무조건 가능하다는 의미다. 만약 2라면 다음 큰 수를 포함하는 것이 최선이 된다. (다음 큰 수를 포함하게 되면 2이상이 되기 때문에 가능한 경우가 존재함 그렇지만 남은 요소로 만들 수 없는 경우가 존재하기 때문에 항상 가능한 것은 아님)
그리고 큰 수를 포함하는 것이 최선인 이유는 빠르게 10이하로 만들 수 있기 때문이다.
그래서 n에서부터 1까지 돌면서 매번 최선의 선택을 해서 0이 되는지 체크하면 불가능한 경우를 구할 수 있고 가능한 경우 최소 몇 번을 이겨야 하는지도 구할 수 있다.
n의 최대 범위는 (10^12 + 10^12)의 제곱근이기 때문에 그리디 + 수학 풀이의 시간 복잡도는 O(약14만)이 된다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static long x, y;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
x = Long.parseLong(st.nextToken());
y = Long.parseLong(st.nextToken());
double sqrt = Math.sqrt(x + y);
if(sqrt != Math.floor(sqrt)) {
System.out.println(-1);
return;
}
int maxI = (int) sqrt;
int cnt = 0;
for(int i=maxI; i>=1; i--) {
if(x == 0) {
break;
}
if(x >= 2 * i - 1 && x - (2 * i - 1) != 2) {
x -= (2 * i - 1);
cnt += 1;
}
}
if(x != 0) {
System.out.println(-1);
} else {
System.out.println(cnt);
}
}
}