[백준 - 14943] 벼룩 시장 - Java

문제 링크

https://www.acmicpc.net/problem/14943

문제

티어: 골드 3
알고리즘: 그리디

벼룩시장에서 사람들이 벼룩을 사고 판다. 놀랍게도 각 사람들이 사려고 하는 벼룩의 합과 파는 벼룩의 합은 같다. 벼룩을 사거나 파는 사람들은 서로 일렬로 길게 서 있으며, 인접한 가게 사이의 거리는 1로 모두 동일하다. 사람들은 움직이지 않고 모든 벼룩 배달을 배달부 기영이에게 맡긴다. 기영이가 두 사람 사이에 벼룩을 배달하는 비용은 (벼룩의 수) * (두 사람 사이의 거리)이다. 모든 벼룩을 사려는 사람에게 배달했을 때, 기영이가 벼룩을 가장 저렴하게 배달하는 비용은 얼마인지 알아보자.

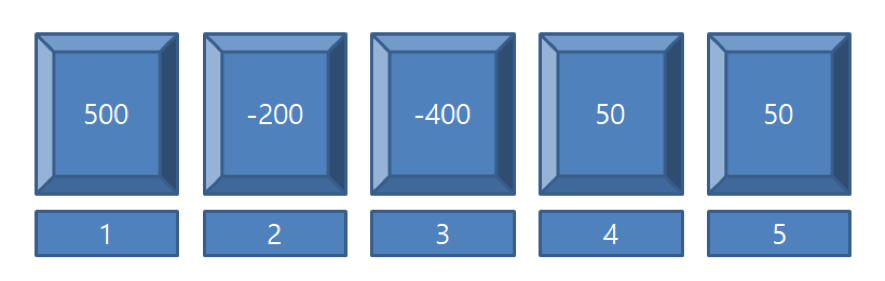
위 예시의 3번 사람은 벼룩 400개를 구하고자 하고, 1번 사람은 500개를 팔고자 한다. 이때 3번 사람이 1번 사람의 벼룩 400개를 살 경우, 벼룩을 옮기는데 드는 비용은 (두 사람 사이의 거리) 2 × (배달하는 벼룩의 수) 400 = 800이 된다.

기영이가 1번 사람에게서 2번 사람에게로 벼룩 200개를 배달하고, 1번, 4번, 5번 사람에게서 3번 사람에게로 각각 300개, 50개, 50개를 배달하면 최소 배달 비용은 200 + 300 × 2 + 50 + 50×2 = 950이다.

입력

첫째 줄에 시작에 존재하는 가게의 개수 N (1 ≤ N ≤ 100,000)가 주어진다.

둘째에는 각 사람이 거래하려는 벼룩의 수 L (-1000 ≤ L ≤ 1000)가 순서대로 주어진다. L이 양수일 경우 벼룩을 파는 사람이며, 음수일 경우 벼룩을 사는 사람이다.

출력

기영이가 벼룩을 전부 배달하는 최소 비용을 출력한다. 출력값은 최대 263-1이며, 이 경우 int 범위를 초과하기 때문에 int 대신 long long을 사용해 출력한다.

풀이

기영이가 벼룩을 가장 저렴하게 배달하는 비용을 구해야 한다.

가장 저렴하게 배달하려면 어떻게 해야 할까?

배달하는 비용의 공식을 보면 (벼룩의 수) * (두 사람 사이의 거리)이다.

벼룩의 합과 파는 벼룩의 합은 같다. 그렇기 때문에 조정할 수 있는 값은 두 사람 사이의 거리이다. 이 거리를 최소로 해서 배달한다면 가장 저렴한 배달 비용이 될 것이다.

예를 들어 입력이 다음과 같을 때

5
500 -200 -400 50 50

먼저, 판매자와 구매자를 나눠준다.

판매자: 500(1), 50(4), 50(5)
구매자: -200(2), -400(3)

구매자는 가까운 거리에 판매자로 부터 벼룩을 사야 한다.

이때 모든 판매자를 탐색하게 된다면 시간 초과가 발생한다.

잘 생각해 보면, 구매자에 인덱스 순서(2 -> 3)로 판매자 인덱스 순서대로 (1 -> 4 -> 5) 벼룩을 산다면, 총이동 거리를 최소화할 수 있다는 것을 알 수 있다.
(인덱스가 앞에 있는 구매자가 인덱스가 앞에 있는 판매자에 벼룩을 사면, 당장은 가장 가까운 판매자 거리가 아닐 수 있어도, 뒷번호 구매자는 뒷번호 판매자에 벼룩을 사게 된다. 그러니까 총거리는 최소가 된다.)

그래서 950이라는 최소 비용을 얻을 수 있다.

그리디 풀이의 시간 복잡도는 O(N)이다.

소스 코드

import java.io.*;
import java.util.*;

class Info {
    int d, l;
    Info(int d, int l) {
        this.d = d;
        this.l = l;
    }
}

public class Main {
    static int N;
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        ArrayList<Info> seller = new ArrayList<>();
        ArrayList<Info> buyer = new ArrayList<>();
        StringTokenizer st = new StringTokenizer(br.readLine());
        for(int i=1; i<=N; i++) {
            int l = Integer.parseInt(st.nextToken());
            if(l >= 0) {
                //벼륙을 파는 사람
                seller.add(new Info(i, Math.abs(l)));
            } else {
                //벼룩을 사는 사람
                buyer.add(new Info(i, Math.abs(l)));
            }
        }
        
        System.out.println(answer(seller, buyer));
    }
    
    static long answer(ArrayList<Info> seller, ArrayList<Info> buyer) {
        long result = 0;
        Stack<Info> stack = new Stack<>();
        for(int i=buyer.size() - 1; i>=0; i--) {
            stack.push(buyer.get(i));
        }
        
        for(int i=0; i<seller.size(); i++) {
            if(seller.get(i).l == 0) {
                continue;
            }
            
            Info byuerInfo = stack.pop();
            while(seller.get(i).l != 0) {
                if(byuerInfo.l >= seller.get(i).l) {
                    //사고도 남는 경우
                    result += (long) Math.abs(byuerInfo.d - seller.get(i).d) * (long) (seller.get(i).l);
                    byuerInfo.l -= seller.get(i).l;
                    seller.get(i).l = 0;
                    stack.push(byuerInfo);
                } else {
                    //다 못사는 경우
                    result += (long) Math.abs(byuerInfo.d - seller.get(i).d) * (long) (byuerInfo.l);
                    seller.get(i).l -= byuerInfo.l;
                    byuerInfo = stack.pop();
                }
            }
        }

        return result;
    }
}