문제 링크
문제
하나의 좌표평면은 다음과 같이 네 개의 사분면으로 나뉜다.!
그러면, 각각의 사분면을 다시 사분면으로 나누어 번호를 붙여 보면 어떨까? 예를 들어 1번 사분면의 1번 사분면은 11번 사분면, 3번 사분면의 2번 사분면은 32번 사분면이라고 하면 좋지 않을까? 물론 한 번 더 나눠 볼 수도 있겠다. 3번 사분면의 4번 사분면의 1번 사분면은 341번 사분면이다.
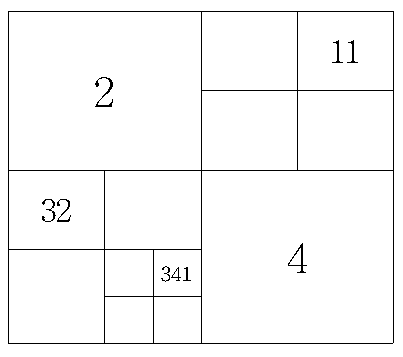
사분면의 번호 길이가 길어짐에 따라 각각의 사분면의 크기는 급격히 작아지며, 그 개수는 기하급수적으로 증가한다.
사분면에 번호를 붙이는 이러한 규칙을 상정하고서, 어떤 사분면 조각을 이동시켰을 때, 그 조각이 위치하게 되는 사분면의 번호가 궁금하다. 예를 들어, 341번 사분면을 오른쪽으로 두 번, 위쪽으로 한 번 이동시키면 424번 사분면에 온다.
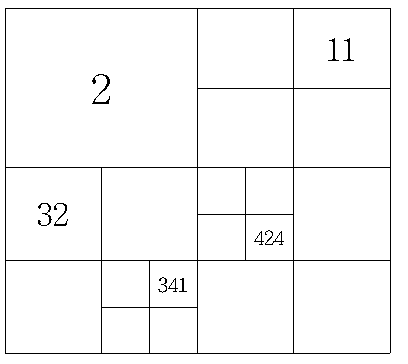
하나의 사분면 조각을 이동시켰을 때, 그 조각이 도착한 사분면의 번호를 알아내는 프로그램을 작성하라.
입력
첫 줄에 이동시키려는 사분면 조각 번호의 자릿수를 나타내는 정수 d와, 그 사분면 조각의 번호가 주어진다. (1 ≤ d ≤ 50) 둘째 줄에는 이동의 내용을 나타내는 두 정수가 x, y가 주어진다. (|x|, |y| ≤ 250) 오른쪽으로 이동한 경우 x가 양수, 왼쪽으로 이동한 경우 음수이며, 그 절댓값은 오른쪽 왼쪽 방향 이동 횟수를 나타낸다. 위쪽으로 이동한 경우 y가 양수, 아래쪽으로 이동한 경우 음수이며, 역시 그 절댓값은 아래위 방향 이동 횟수를 나타낸다.
출력
첫 줄에 도착한 사분면의 번호를 출력한다. 만약, 존재하지 않는 사분면인 경우에는 -1을 출력한다.
알고리즘: 수학, 분할정복
풀이
먼저 입력에 주어진 사분면 조각의 좌표를 찾아야 한다.
(좌표의 범위는 x -> 0 ~ side -1, y -> 0 ~ side //side = 2의 d 승임)
TC
3 341
2 1 로 예를 들면 341의 좌표를 먼저 찾아야 하는데, 맨 앞에 조각부터 본다.
341에 3분 면은 초기 좌표(0, 0)라 할 때 (0, 0 + side/2)에 존재한다.
target을 업데이트시켜준다. 그리고 side를 side/2로 업데이트해 준다.
위 방식을 반복하면서 side/2 == 0이 되면 반복을 종료시켜준다.
341의 2 1 만큼 이동시키면 그 좌표는 (5,5)가 된다. 이 좌표가 target 우리가 찾고자 하는 좌표이고 이 좌표값이 범위에 만족한다면, 이제 반대로 목표 좌표에 조각을 찾아야 한다.
(5, 5)를 side/2로 나눈다.(side는 max_side임) 그러면 (1,1)이 되고 (1,1)은 4분면에 해당한다. //(1,0)은 1분면, (0,0)은 2분면, (0,1)은 3분면, (1,1)은 4분면에 해당함
4를 추가해주고, 다음 조각을 찾기위해서 (5,5)를 (5-side/2, 5-side/2)로 side는 side/2로 업데이트해 준다. => 4분면은 위치상 x, y 값 둘 다 side/2만큼 빼줘야 함.
위 방식을 반복하면서 side/2 == 0이면 반복을 종료시키고 지금까지 찾은 조각을 출력한다.
소스 코드
import java.io.*;
import java.util.*;
class Coordinate {
long x,y;
Coordinate(long x, long y) {
this.x = x;
this.y = y;
}
}
public class Main {
static int d;
static int num[];
static String str_num;
static Coordinate target = new Coordinate(0,0);
static Coordinate w_cdn;
static long max_side;
static StringBuilder ans = new StringBuilder();
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
d = Integer.parseInt(st.nextToken());
max_side = (long) Math.pow(2, d);
num = new int[d];
str_num = st.nextToken();
for(int i=0; i<str_num.length(); i++) {
num[i] = str_num.charAt(i) - '0';
}
StringTokenizer sti = new StringTokenizer(br.readLine());
w_cdn = new Coordinate(Long.parseLong(sti.nextToken()), Long.parseLong(sti.nextToken()) * -1);
find_coordinate(0, max_side);
target = new Coordinate(target.x + w_cdn.x, target.y + w_cdn.y);
if((target.x >=0 && target.x <= max_side - 1) && (target.y >=0 && target.y <= max_side -1)) {
find_num(max_side);
System.out.println(ans.toString());
} else System.out.println(-1);
}
static void find_coordinate(int ind, long side) {
if(side/2 == 0) return;
if(num[ind] == 1) {
target = new Coordinate(target.x + side/2, target.y);
find_coordinate(ind+1, side/2);
} else if(num[ind] == 2) {
target = new Coordinate(target.x, target.y);
find_coordinate(ind+1, side/2);
} else if(num[ind] == 3) {
target = new Coordinate(target.x, target.y + side/2);
find_coordinate(ind+1, side/2);
} else {
target = new Coordinate(target.x + side/2, target.y + side/2);
find_coordinate(ind+1, side/2);
}
}
static void find_num(long side) {
if(side/2 == 0) return;
Coordinate s_cdn = new Coordinate(target.x/(side/2), target.y/(side/2));
if(s_cdn.x == 0 && s_cdn.y == 0) {
ans.append('2');
target = new Coordinate(target.x, target.y);
find_num(side/2);
} else if(s_cdn.x == 0 && s_cdn.y == 1) {
ans.append('3');
target = new Coordinate(target.x, target.y - side/2);
find_num(side/2);
} else if(s_cdn.x == 1 && s_cdn.y == 0) {
ans.append('1');
target = new Coordinate(target.x - side/2, target.y);
find_num(side/2);
} else if(s_cdn.x == 1 && s_cdn.y == 1) {
ans.append('4');
target = new Coordinate(target.x - side/2, target.y - side/2);
find_num(side/2);
}
}
}