문제 링크
문제
티어: 골드 3
알고리즘: 누적합, 그리디
킬로와 헥토는 좀비 떼로부터 탄약고를 사수하는 데에 성공했다. 포상 휴가나 조기 전역을 기대했으나 좀비 사태로 인해 계엄령이 선포되면서 오히려 전역이 연기되고 기관총 진지에 배치되었다.
전역이 연기된 킬로와 헥토에게 좀비 떼가 다가오기 시작했다.
기관총 진지 앞쪽 길의 거리는 L m이며, 진지로부터 i m 떨어진 곳에 있는 좀비의 체력은 Zi이다. 체력이 0 이하가 된 좀비는 영구적으로 죽는다.
기관총 진지에서 킬로와 헥토는 좀비가 1 m 이동할 때 기관총 또는 수평 세열 지향성 지뢰를 한 번 사용할 수 있다. 수평 세열 지향성 지뢰를 격발하는 경우 후폭풍을 피하기 위해 킬로와 헥토는 기관총 진지 밑으로 숨어야 한다. 즉, 수평 세열 지향성 지뢰 격발과 기관총 사격을 동시에 할 수는 없다.
- 기관총
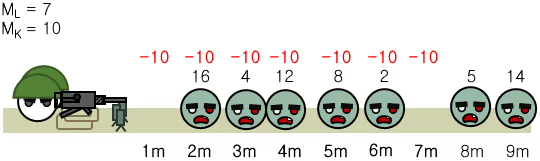
유효 사거리는 진지 앞으로부터 ML m이다. 유효 사거리 내의 각 1 m 마다 좀비의 체력을 MK만큼 낮춘다.
기관총 탄약은 엄청나게 많이 있으므로 신경쓰지 않아도 된다. 총열 교체나 장전, 총기 이상 등을 고려할 필요 없이 계속 사격할 수 있다고 가정한다.
- 수평 세열 지향성 지뢰
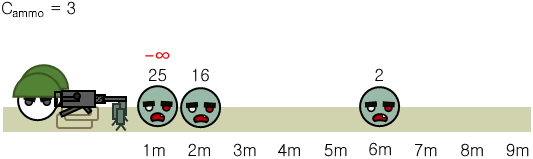
유효 사거리는 진지 앞으로부터 1 m이다. 하지만 진지 바로 앞 1 m의 좀비는 체력과 상관없이 제압할 수 있다.
수평 세열 지향성 지뢰는 Cammo개 있다.
기관총 진지라곤 하나 콘크리트로 지어진 토치카가 아니라 사대로 구축한 임시 진지이기 때문에 1 m 떨어진 길 위의 좀비를 제압하지 못한다면 사망한다.
과연 킬로와 헥토는 살아남을 수 있을까?
입력
첫 번째 줄에는 기관총 진지 앞쪽 길의 거리를 나타내는 정수 L (1 ≤ L ≤ 3 × 106)이 주어진다.
두 번째 줄에는 기관총의 유효 사거리를 나타내는 정수 ML (1 ≤ ML ≤ 3 × 106)과 각 1 m 당 살상력을 나타내는 정수 MK (1 ≤ MK ≤ 100)가 빈칸을 사이에 두고 주어진다.
세 번째 줄에는 수평 세열 지향성 지뢰의 개수 Cammo (0 ≤ Cammo ≤ 3 × 106)가 주어진다.
네 번째 줄부터 L개의 줄에 걸쳐서 정수가 하나씩 주어진다. 이 때 i (1 ≤ i ≤ L)번째 정수는 기관총 진지에서 i m 떨어진 곳의 좀비의 체력 Zi (0 ≤ Zi ≤ 3 × 108)이다. Zi가 0인 경우 i m 떨어진 곳에 좀비가 없다는 뜻이다.
출력
킬로와 헥토가 살아남을 수 있다면 YES, 살아남을 수 없다면 NO를 출력한다.
풀이
구하고자 하는 것은 킬로와 헥토가 살아남을 수 있는지다. 그러니까 최선의 선택을 통해 최대한 살아남을 수 있게 했을 때 결과를 출력하면 된다.
최선의 선택이란 폭탄 (수평 세열 지행성 지뢰)을 쓰는 타이밍을 말한다.
언제 사용하는게 좋을까?
만약 1m까지 왔는데 좀비의 체력이 0이 아니라면 이때는 폭탄을 써야하며 이 타이밍이 최선의 타이밍이라 할 수 있다.
아이디어는 매우 간단하지만, 폭탄을 사용할 타이밍에는 기관총을 사용하지 못하기 때문에 기관총에 누적 데미지 계산이 까다로워 진다.
예를 들어 7m에 좀비가 있고, 사거리 5에, 데미지 3이면 간단하게 기관총 누적 데미지를 구할 수 있다. (5 * 3 = 15) 하지만 폭탄을 사용하게 되면서 사용했을 때 기관총 유효 사거리에 있는 좀비들은 기관총을 맞지 않게 된다. 그래서 폭탄을 고려한 계산이 필요하다.
폭탄이 사용되면 기관총 유효 사거리만큼 기관총을 한대 덜 맞게 된다.
이를 다음과 같이 표현할 수 있다.
1m 2m 3m(zombi) 4m 5m
3m에 있는 zombi가 1m에 왔을 때 죽지 않는다면 폭탄을 사용해야 됨
폭탄이 사용되면 (3m ~ 3m + 유효 사거리 - 1) 이 범위에 좀비들이 기관총을 한대 덜 맞음
그러면 4m를 계산할 때는 3m에 폭탄 누적 개수 더해주고, 5m를 계산할 때는 4m에 폭탄 누적 개수를 더해준다. 여기서 누적합이 사용된다.
그리고 (3m ~ 3m + 유효 사거리 - 1) 이 범위외에는 폭탄에 영향 받지 않기 때문에 폭탄 누적 개수를 -1 해야 한다. 이때 누적합을 사용하기 때문에 전부 -1를 해줄 필요는 없고 sumCammo[3m + 유효 사거리] -= 1만 해주면 된다.
누적합, 그리디 알고리즘 풀이의 시간 복잡도는 O(L)이다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int L, Ml, Mk, Cammo; // Ml은 기관총의 유효 사거리, Mk는 1m당 살상력, Cammo 폭탄 개수
static int[] zombi; //좀비 체력
static int[] sumCa; //폭탄 누적합
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
L = Integer.parseInt(br.readLine());
zombi = new int[L + 1];
sumCa = new int[L + 1];
StringTokenizer st = new StringTokenizer(br.readLine());
Ml = Integer.parseInt(st.nextToken());
Mk = Integer.parseInt(st.nextToken());
Cammo = Integer.parseInt(br.readLine());
for(int i=1; i<=L; i++) {
zombi[i] = Integer.parseInt(br.readLine());
}
System.out.println(gameStart());
}
static String gameStart() {
for(int i=1; i<=L; i++) {
sumCa[i] += sumCa[i - 1]; //폭탄 개수 누적합
int w = i;
if(w > Ml) {
//유호사거리보다 길다면
w = Ml;
}
int damege = w * Mk - (sumCa[i] * Mk); //1m까지 좀비가 왔을 때 받는 총 데미지
int left = zombi[i] - damege;
if(left > 0) {
//죽지 않았다면 폭탄을 사용하는 것이 최선의 선택임
if(Cammo > 0) {
//폭탄 있으면 유효사거리까지만 폭탄이 누적되게
sumCa[i] += 1;
if(i + Ml <= L) {
sumCa[i + Ml] -= 1;
}
Cammo -= 1;
} else {
//폭탄이 없으면 게임 끝
return "NO";
}
}
}
return "YES";
}
}