문제 링크
문제
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.
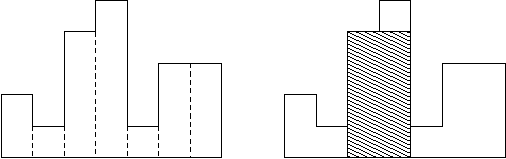
히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.
입력
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.
출력
각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.
알고리즘: 자료 구조
풀이
증명과 구현이 까다로운 문제다. 직사각형의 수가 최대 100,000개이기 때문에, n^2풀이는 정답을 될 수 없다. 그러면 nlogn이나, n풀이의 포커스를 두고 풀이를 생각해야 한다.
만약 직사각형의 높이가 오름차순으로 놓여있다고 생각해보자, 오름차순으로 직사각형이 놓여있다면, check하는 현재 막대의 높이와 n만으로 최대 넓이를 구할 수 있다. (O(n)으로 가능)
ex) 1번째 직사각형의 높이가 5이고 n이 10이면 1번째 직사각형을 포함한 최대 넓이는 50이다.
그러면 우리는 위 방법을 적극적으로 활용해야 한다. stack자료구조에 직사각형의 인덱스를 넣는데, stack안에 직사각형은 오름차순을 유지해야 한다. 즉 stack의 top부분 직사각형과 check하는 직사각형의 높이를 비교한다. 만약 check하는 직사각형이 더 크다면 그대로 넣어주고, 그렇지 않다면 stack안에 check하는 직사각형의 높이보다 큰 직사각형을 모두 pop해준다. -> (stack안에 직사각형을 오름차순으로 유지시키기 위해서) 그리고 pop을 해줄 때 그 넓이를 구해서, 최대 넓이를 갱신해주면 된다.
ex) stack = {1->(1), 2->(4), 3->(5)}, check 4->(1), 5 > 1이기 때문에 pop을 해준다.
높이가 5인 직사각형의 너비는 (3 - 2)다. -> (여기서 2는 어디서 나왔냐? 높이가 5인 직사각형보다 작은 직사각형의 인덱스가 peek를 했을 때 값이기 때문에 그 값이 2이다. 그래서 너비가 3-2가 되는 것이다.) 그래서 높이가 5인 직사각형을 포함한 최대 넓이는 5 * 1 = 5다.
이런 식으로 pop을 해주면서 최대 넓이를 갱신해주면 된다.
O(n)풀이기 때문에 TLE없이 통과할 수 있다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int N;
static long height[];
static ArrayList < Integer > list;
static long ans;
static StringBuilder sb = new StringBuilder();
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
while (true) {
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
if (N == 0) break;
height = new long[N];
list = new ArrayList < > ();
ans = 0;
for (int i = 0; i < N; i++) height[i] = Long.parseLong(st.nextToken());
for (int i = 0; i < N; i++) {
if (list.size() == 0) list.add(i);
else {
if (height[i] <= height[list.get(list.size() - 1)]) {
int max_width = list.get(list.size() - 1) + 1;
while (true) {
int ck_ind = list.get(list.size() - 1);
if (height[i] > height[ck_ind]) break;
list.remove(list.size() - 1);
if (list.size() == 0) {
ans = Math.max(ans, height[ck_ind] * (long) max_width);
break;
} else {
int peek = list.get(list.size() - 1) + 1;
ans = Math.max(ans, height[ck_ind] * (long)(max_width - peek));
}
}
}
list.add(i);
}
}
if (list.size() != 0) {
int max_width = list.get(list.size() - 1) + 1;
while (true) {
int ind = list.get(list.size() - 1);
list.remove(list.get(list.size() - 1));
if (list.size() == 0) {
ans = Math.max(ans, height[ind] * (long) max_width);
break;
} else {
int peek = list.get(list.size() - 1) + 1;
ans = Math.max(ans, height[ind] * (long)(max_width - peek));
}
}
}
sb.append(ans + "\n");
}
System.out.println(sb.toString().trim());
}
}