문제 링크
문제
티어: 골드 2
알고리즘: 그리디, 수학, 정수론

입력

출력
N에 도달하기 위한 최소 비용을 출력합니다.
풀이
N에 도달하기 위한 최소 비용을 출력해야 한다.
일단 불가능한 경우는 없다. 왜냐하면 1에서부터 N까지 도달하는 데 1씩 더할 수 있기 때문이다.
나는 이 문제를 탑 다운 방식으로 접근해 봤다.
N 바로 전에 어떠한 값이 최선의 선택이 될까?
일단 a는 b보다 크거나 같기 때문에 a는 최소 N/2만큼을 갖는다.
예를 들어 설명하겠다. N이 16이라면
16 전의 값은 N/2 이상을 가져야 된다. 그래서 a는 최소 4가되고, b는 최대 4가 된다.
a의 후보의 따른 b의 쌍을 나열하면 (a, b)
(4, 4) -> 1p
(8, 2) -> 4p
(16, 1) -> 16p
이 있는데 b가 클 수록 point는 최소가 된다.
그래서 직감적으로 b가 큰 경우를 선택하는 것이 최선이지 않을까? 생각했다.
그런데 한 가지 의문이 들었다.
b가 더 큰 것보다 작은 것을 선택했을 때 그 다음 point가 작아지는 경우가 있지 않을까?
증명해 본 결과 없다는 것을 알게됐다.
그 과정을 간략하게 설명하자면,
만약, (16, 1)을 선택하는 경우 N은 1이 감소하고, 16p를 얻는다.
여기서 b가 1씩 증가하면 a는 약1/2, 1/3 .. (그 보다 더 작은 값일 것이다)로 감소할 것인다.
그래서 b가 더 큰 값을 선택했을 때 더 작은 값을 선택했을 때의 경로까지 가는데 b=1로 가더라도
포인트는 무조건 작을 수 밖에 없다.
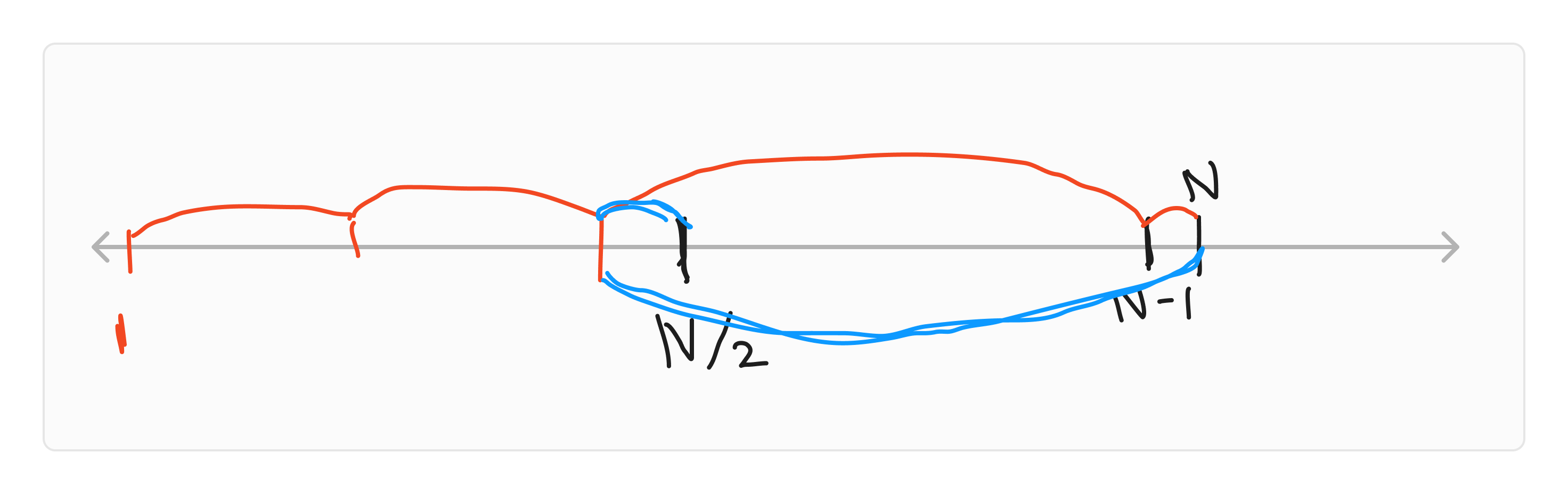
즉, 최선의 선택은 b가 가장 큰 것을 선택하는 것이다.
이 풀이의 시간 복잡도는 O(N)보다 작을 것이다. (a, b) 쌍을 모든 지점에서 찾는다 했을 때 O(N)이 되는데, 그럴 일이 없기 때문이다. (홀수 + 1은 짝수여서)
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int N;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
int cnt = 0;
while (N != 1) {
int c = N % 2 == 0 ? N / 2 : N / 2 + 1;
int a = N / 2;
while (c % a != 0) {
c += 1;
a -= 1;
}
N = c;
cnt += c / a;
}
System.out.println(cnt);
}
}