문제 링크
문제
티어: 골드 2
알고리즘: 그리디, 수학

입력
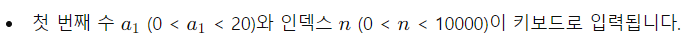
출력
an 값을 한 줄에 출력하세요.
추가 조건
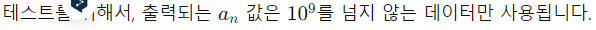
풀이
a1과 n이 주어졌을 때 조건을 만족하는 an을 구해야 한다.
ai는 ai-1과 같은 자릿수를 가질 수 있고, +1 자릿수를 가질 수 있다. (+2인 경우는 없다. x4이기 때문)
같은 자릿수인 경우부터 보면
일단 같은 자릿수에서 2번 째 조건을 만족하기 위해 빼야될 총 횟수를 구해야 한다.
예를 들어 a1 = 15라면 a2의 자릿수 합은 6이고 되고, a1의 자릿수는 2이기 때문에 총 빼야될 횟수는 9 * 2 - 6 = 12가 된다.
그래서 99에서 각 자릿수에서 차감시키는 횟수의 총합을 12로 만들면 자릿수의 합은 6이 되는 것이다.
그러면 가중치가 가장 큰 첫 번째 자릿수에서는 얼마나 빼야될까?
ai는 가장 작은 정수이고, ai-1보다는 커야되기 때문에 9 - (ai-1의 첫 번째 자릿수)가 된다.
이 값은 max로 뺄 수 있는 횟수이기 때문에 아직 답이 될 수는 없다.
그래서 일단 빼고, 남은 횟수가 0인지를 판단해야 한다.
12에서 8을 빼면 4가 남고, 현재 수는 19가 된다. 이제 두 번째 자릿수를 빼야 하는데 두 번째 자릿수는 마지막 자릿수이며 ai-1보다는 커야되기 때문에 9 - (ai-1의 두 번째 자릿수) - 1이 된다.
그래서 max로 뺄 수 있는 횟수는 3이 된다. (5보다 커야되기 때문에 4보다는 덜 빼야됨)
3을 빼면 16이 되고, 남은 횟수는 1이 되어서 이 경우 답이 될 수 없다.
그러면 이제 일의 자리에서 바로 앞 자릿수의 차감 횟수를 - 1 해야한다. 왜냐하면 일의 자릿수의 최대 차감 횟수가 9로 증가해서 가능성을 높일 수 있기 때문이다.
그래서 9 - (ai-1의 첫 번째 자릿수) - 1을 하면 max로 뺄 수 있는 횟수는 7이 되고,
29이며, 남은 횟수는 5가 남는다.
ai의 첫 번째 자릿수가 ai-1 첫 번째 자릿수보다 크기 때문에 그 뒷 자릿수는 어떠한 값이 와도 상관 없다. 그래서 두 번째 자릿수의 최대 차감 횟수는 9가 된다.
남은 횟수는 5이기 때문에 답은 24가 되며, 남은 횟수는 0으로 가능한 답이 된다.
그래서 a1이 15라면 a2는 24가 되는 것이다.
+1 자릿수인 경우는 어떻게 수를 배치해도 ai-1보다 크기 때문에 모든 자릿수의 최대 차감 횟수는 9가 된다. 당연히 가중치가 큰 자릿수부터 차감 횟수를 적용해 주면된다.
이 풀이의 시간 복잡도는 O(N)이다.
ai를 구할 때 최대 자릿수 * 자릿수만큼 반복하고, an의 값은 10^9를 넘지 않기 때문이다.
소스 코드
import java.io.*;
import java.util.*;
class Num {
String strNum;
int sum, len; //자릿수의 합
Num(String strNum) {
this.strNum = strNum;
this.sum = getDigitsSum(strNum);
this.len = strNum.length();
}
static public int getDigitsSum(String strNum) {
int result = 0;
for(int i=0; i<strNum.length(); i++) {
result += strNum.charAt(i) - '0';
}
return result;
}
}
public class Main {
static int a, n;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
Num before = new Num(st.nextToken()); //a1 -> ai - 1
n = Integer.parseInt(st.nextToken());
for(int r=2; r<=n; r++) {
//a2~an까지
StringBuilder sb = new StringBuilder();
int len = before.len;
int reqSum = Num.getDigitsSum(String.valueOf(Long.parseLong(before.strNum) * (long) 4)); //필요한 합 ai-1 * 4의 자릿수 함
int subCnt = len * 9 - reqSum; // 뺄 횟수 -> 이게 0이 되어야 자릿수의 합이 reqSum이 됨. 9 9 9..에서
if(subCnt >= 0) {
int spot = len - 1; //이 부분은 항상 전에 값의 자릿수보다 +1을 가져야됨 2번째 조건을 만족하기 위함
//spot + 1 이상부터는 최대 자리수 차감 횟수가 9가 된다.
while(spot >= 0) {
if(before.strNum.charAt(spot) == '9') {
//9인 경우에 +1하면 다음 자릿수가 +1되기 때문에 다음 자릿수로 넘겨준다.
spot -= 1;
continue;
}
int copySubCnt = subCnt;
for(int i=0; i<len; i++) {
int subDigMax = 9 - (before.strNum.charAt(i) - '0'); //각 자릿수마다 최대로 뺄 수 있는 횟수;
if(i == spot) {
subDigMax -= 1;
} else if(spot + 1 <= i) {
subDigMax = 9;
}
int subDigCnt = copySubCnt >= subDigMax ? subDigMax : copySubCnt; //실제로 뺄 횟수
copySubCnt -= subDigCnt;
sb.append(9 - subDigCnt);
}
if(copySubCnt == 0) {
break;
}
sb = new StringBuilder();
spot -= 1;
}
if(spot == -1) {
len += 1;
}
} else {
len += 1;
}
if(before.len + 1 == len) {
//이 경우는 ai-1보다 자릿수가 하나 더 있는 경우임 그래서 무조건 가능함.
subCnt = len * 9 - reqSum;
for(int i=0; i<len; i++) {
int subDigMax =9; //각 자릿수마다 최대로 뺄 수 있는 횟수;
if(i == 0) {
subDigMax -= 1; //가장 앞의 자릿수는 0이 될 수 없음
}
int subDigCnt = subCnt >= subDigMax ? subDigMax : subCnt; //실제로 뺄 횟수
subCnt -= subDigCnt;
sb.append(9 - subDigCnt);
}
}
before = new Num(sb.toString());
}
System.out.println(before.strNum);
}
}