문제 링크
문제
상근이는 감옥에서 죄수 두 명을 탈옥시켜야 한다. 이 감옥은 1층짜리 건물이고, 상근이는 방금 평면도를 얻었다.
평면도에는 모든 벽과 문이 나타나있고, 탈옥시켜야 하는 죄수의 위치도 나타나 있다. 감옥은 무인 감옥으로 죄수 두 명이 감옥에 있는 유일한 사람이다.
문은 중앙 제어실에서만 열 수 있다. 상근이는 특별한 기술을 이용해 제어실을 통하지 않고 문을 열려고 한다. 하지만, 문을 열려면 시간이 매우 많이 걸린다. 두 죄수를 탈옥시키기 위해서 열어야 하는 문의 개수를 구하는 프로그램을 작성하시오. 문을 한 번 열면 계속 열린 상태로 있는다.
입력
첫째 줄에 테스트 케이스의 개수가 주어진다. 테스트 케이스의 수는 100개를 넘지 않는다.
첫째 줄에는 평면도의 높이 h와 너비 w가 주어진다. (2 ≤ h, w ≤ 100) 다음 h개 줄에는 감옥의 평면도 정보가 주어지며, 빈 공간은 '.', 지나갈 수 없는 벽은 '*', 문은 '#', 죄수의 위치는 '$'이다.
상근이는 감옥 밖을 자유롭게 이동할 수 있고, 평면도에 표시된 죄수의 수는 항상 두 명이다. 각 죄수와 감옥의 바깥을 연결하는 경로가 항상 존재하는 경우만 입력으로 주어진다.
출력
각 테스트 케이스마다 두 죄수를 탈옥시키기 위해서 열어야 하는 문의 최솟값을 출력한다.
알고리즘: BFS, 다익스트라
풀이
먼저 이 문제는 최단 거리가 아니고, 문의 최솟값을 구하는 문제이다. 즉 빠르게 나가는 게 중요한 게 아니다. 문의 최솟값은 다익스트라 알고리즘을 이용하는데, 여기서 죄수가 두 명이기에 문제가 많이 까다로워진다.
결론만 말하자면, 제3자 상근이가 필요하다.
그리고 상근이, 죄수1, 죄수2 각각 BFS를 돌리고, 다익스트라로 구한 좌표별 최소값을 다 더해주면 된다. 먼저 이 풀이가 왜 가능하냐?
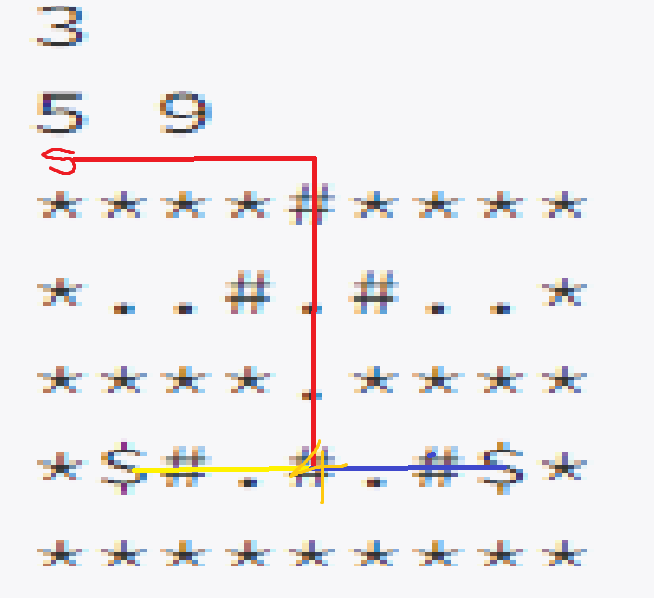
상근이라는 제3자를 감옥 밖에서부터 다익스트라를 이용해 최소 비용 경로를 구하면 상근이는 감옥 밖에서 감옥안으로 들어왔기 때문에 그 경로 자체가 탈출구가 된다. 그리고 상근이와 죄수1 죄수2가 만나는 부분 중 최솟값을 구하면 그 값이 문의 최솟값이 된다.
그래서 만나는 부분을 어떻게 구하냐? 만나는 부분은 죄수1 죄수2도 각각 다익스트라로 최소 비용 경로를 구하고, 상근 + 죄수1 + 죄수2의 최소 비용 거리를 다 더해주면 그 값이 만나는 부분 중 최소 비용이 되는 것이다. 주의할점은 문이 있는 좌표의 값은 -2를 해야한다. 왜냐하면 문은 한 번 열면 열린 상태로 있기 때문에 열린 문은 카운트하면 안 된다. 여기서 문이 아닌 좌표 또한 독립적으로 문을 열고 카운트를 해줬는데 최소 비용 거리를 다시 구해야 하는 거 아니냐고 의문이 들 수 있다. 하지만 어차피 문이 존재하면 그 좌표가 최솟값이 되고, 문이 없다고 하면 문을 열지 않았기 때문에 -해줄 값 또한 없다. 그렇기 때문에 문이 있는 좌표만 -해주는 것이다.
소스 코드
import java.io.*;
import java.util.*;
class Node {
int x,y,c;
Node(int x, int y, int c) {
this.x = x;
this.y = y;
this.c = c;
}
}
public class Main {
static final int dx[] = {-1, 0, 1, 0};
static final int dy[] = {0, -1, 0 ,1};
static int T, H, W;
static char map[][];
static int dks[][];
static int dks_sum[][];
static ArrayList<Node> list;
static int ans;
public static void main(String args[])throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
T = Integer.parseInt(br.readLine());
for(int c=0; c<T; c++) {
StringTokenizer st = new StringTokenizer(br.readLine());
H = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
map = new char[H+2][W+2];
dks = new int[H+2][W+2];
dks_sum = new int[H+2][W+2];
list = new ArrayList<>();
list.add(new Node(0,0,0)); //상근이
for(int i=0; i<map.length; i++) {
if(i==0 || i== map.length-1) {
for(int j=0; j<map[i].length; j++) {
map[i][j] = '.';
}
} else {
String input = br.readLine();
for(int j=0; j<map[i].length; j++) {
if(j==0 || j== map[i].length-1) map[i][j] = '.';
else {
map[i][j] = input.charAt(j-1);
if(map[i][j]=='$') list.add(new Node(j,i,0)); //죄수
if(map[i][j]=='#') dks_sum[i][j] = -2;
}
}
}
}
//최솟값 구하기
for(int i=0; i<list.size(); i++) {
dks_init(); //초기화
BFS(list.get(i));
for(int j=0; j<dks.length; j++) {
for(int k=0; k<dks[i].length; k++) {
dks_sum[j][k] += dks[j][k];
}
}
}
ans = 10001;
for(int i=0; i<dks_sum.length; i++) {
for(int j=0; j<dks_sum[i].length; j++) {
ans = Math.min(ans, dks_sum[i][j]);
}
}
System.out.println(ans);
}
}
static void BFS(Node start) {
Queue<Node> que = new LinkedList<>();
que.add(start);
dks[start.y][start.x] = 0;
while(que.size()!=0) {
Node n = que.poll();
for(int i=0; i<4; i++) {
int nx = n.x + dx[i];
int ny = n.y + dy[i];
if((nx>=0 && nx<=W+1) && (ny>=0 && ny<=H+1)) {
if(map[ny][nx]=='.' || map[ny][nx]=='$') {
//빈공간
if(n.c<dks[ny][nx]) {
que.add(new Node(nx, ny, n.c));
dks[ny][nx] = n.c;
}
} else if(map[ny][nx]=='#') {
//문
if(n.c+1<dks[ny][nx]) {
que.add(new Node(nx, ny, n.c+1));
dks[ny][nx] = n.c+1;
}
}
}
}
}
}
static void dks_init() {
for(int i=0; i<dks.length; i++) {
Arrays.fill(dks[i], 10001);
}
}
}