문제 링크
문제
N×M 보드 위에서 할 수 있는 게임이 있다. 보드는 크기가 1×1인 정사각형 칸으로 나누어져 있다. 보드의 각 칸은 빈 칸 또는 장애물이다. 장애물은 아래 그림에선 어두운 사각형으로 표시되어져 있다.
게임을 시작하려면 보드의 빈 칸 위에 공을 하나 놓아야 한다. 아래 그림에서 공은 회색 점으로 표시되어져 있다. 게임은 단계로 이루어져 있고, 각 단계는 아래와 같이 구성되어져 있다.
- 위, 아래, 오른쪽, 왼쪽 중 방향 하나를 고른 다음, 그 방향으로 공을 계속해서 이동시킨다.
- 공은 장애물, 보드의 경계, 이미 공이 지나갔던 칸을 만나기 전까지 계속해서 이동한다.
게임은 공이 더 이상 이동할 수 없을 때 끝난다. 이 때, 모든 빈 칸을 공이 방문한 적이 있어야 한다.
아래 그림은 총 10단계 만에 모든 칸을 방문하는 방법이다.
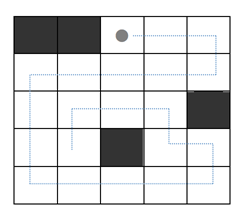
보드의 상태가 주어졌을 때, 모든 칸을 방문하기 위한 이동 횟수의 최솟값을 구하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다.
각 테스트 케이스의 첫째 줄에는 보드의 크기를 나타내는 N과 M이 주어진다. N은 세로 크기, M은 가로 크기이고, 두 값은 30보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 상태가 주어진다. 보드의 상태는 장애물을 나타내는 '*'과 빈 칸을 나타내는 '.'으로 이루어져 있다.
입력으로 주어진 보드가 장애물로만 이루어진 경우는 없다.
출력
각 테스트 케이스마다 보드의 모든 빈 칸을 방문하는 최소 이동 횟수를 출력한다. 출력 형식은 예제를 참고한다.
만약, 모든 빈 칸을 방문할 수 없다면 최소 이동 횟수는 -1이다. 가능한 이동 경로의 수는 1,000,000개를 넘지 않는다.
알고리즘: 구현, 백트래킹
풀이
모든 빈칸에 공을 놓아보고, 그 위치에서 갈 수 있는 모든 경우의 수를 구하면 된다.
시간 복잡도를 대략 짐작해보면 한 번 방향을 정하면 약 30만큼 이동한다.
그러면 약 30번 반복하고, 갈 수 있는 방향은 최대 두 방향이고, 대부분의 방향이 한 방향으로 예상된다. 대충 두 방향인 경우를 반으로 잡아도 2^15으로 시간 초과 브루트 포스 방식으로 충분히 가능하다.
어림잡아서 계산했기 때문에 오차가 있을 수 있지만, 확실한 건 모든 경우의 수를 구해도 통과 가능함
소스 코드
import java.io.*;
import java.util.*;
class Coordinate {
int x, y;
Coordinate(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
static final int dx[] = {
-1,
0,
1,
0
};
static final int dy[] = {
0,
-1,
0,
1
};
static int N, M;
static char board[][];
static int ans = 1000001;
static ArrayList < Coordinate > blank = new ArrayList < > ();
static StringBuilder sb = new StringBuilder();
static int count = 1;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
while (true) {
String str_input = br.readLine();
if (str_input == null) break;
else {
StringTokenizer st = new StringTokenizer(str_input);
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
board = new char[N][M];
for (int i = 0; i < N; i++) {
String input = br.readLine();
for (int j = 0; j < M; j++) {
board[i][j] = input.charAt(j);
if (board[i][j] == '.') blank.add(new Coordinate(j, i));
}
}
for (int i = 0; i < blank.size(); i++) {
int x = blank.get(i).x;
int y = blank.get(i).y;
board[y][x] = '*';
DFS(x, y, 0);
board[y][x] = '.';
}
if(ans == 1000001) {
sb.append("Case " + String.valueOf(count) + ": -1\n" );
blank = new ArrayList<>();
} else {
sb.append("Case " + String.valueOf(count) + ": " + String.valueOf(ans) + "\n");
blank = new ArrayList<>();
ans = 1000001;
}
count += 1;
}
}
System.out.println(sb.toString().trim());
}
static void DFS(int x, int y, int cout) {
if (check()) {
if (ans > cout) ans = cout;
return;
}
for (int i = 0; i < 4; i++) {
int nx = x;
int ny = y;
ArrayList < Coordinate > back = new ArrayList < > ();
while (true) {
nx += dx[i];
ny += dy[i];
if (((nx >= 0 && nx <= M - 1) && (ny >= 0 && ny <= N - 1)) && board[ny][nx] == '.') {
board[ny][nx] = '*';
back.add(new Coordinate(nx, ny));
} else {
if (back.size() == 0) break;
else {
DFS(nx - dx[i], ny - dy[i], cout + 1);
for (int j = 0; j < back.size(); j++) {
board[back.get(j).y][back.get(j).x] = '.';
}
break;
}
}
}
}
}
static boolean check() {
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[i].length; j++) {
if (board[i][j] == '.') return false;
}
}
return true;
}
}