[프로그래머스] 카드 짝 맞추기 - Java

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/72415

문제

링크 참조

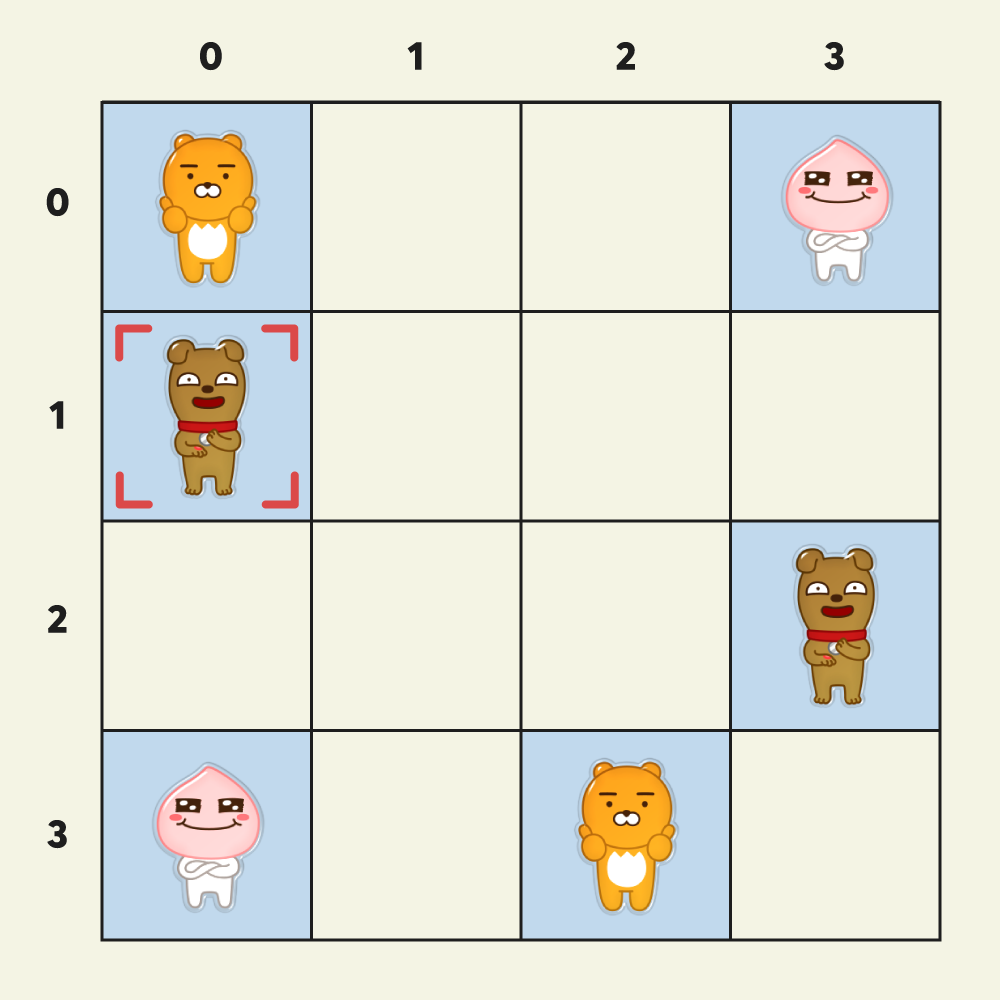
제한사항

링크 참조

알고리즘: BFS, 비트 마스킹

풀이

카드를 모두 제거하기 위한 최소 연산 횟수를 구하는 게 문제의 목표다.
연산은 총 3개 존재하고, 모든 연산의 가중치는 1이다. 즉 가장 먼저 목표에 도달한 노드가 최소 연산 횟수가 된다는 의미다. -> BFS를 이용한다.

하지만 각 노드에서 모든 연산을 중복 처리 없이 한다면 당연히 시간 초과가 발생한다.
중복 처리 아이디어가 이 문제의 핵심이다.

내가 생각한 아이디어는 이렇다.
1. 카드는 앞면이거나, 뒷면이다. -> (짝을 맞추어 사라진 카드 또한 앞면이라고 가정한다.)
2. 그러면 4x4 모든 좌표는 2가지 상태로 존재 한다. 이 말은 즉 비트 마스킹을 이용해서 중복 처리가 가능 하다는 의미다. -> (이 경우의 수는 2^0 ~ 2^15의 합으로 약 60000이다.);
3. 또 한가지 고려해 줄 점은 현재 커서의 위치다. 보드가 같은 상태라도 커서 위치에 따라 다르다.

중복 처리를 했을 때 모든 경우의 수는 60000 4 4로 충분히 가능한 풀이다.

그러면 위 아이디어로 중복 처리를 하고, BFS를 구현하면 된다.

소스 코드

import java.util.*;
class Node {
    int x, y, c, set, select;
    Node(int x, int y, int c, int set, int select) {
        this.x = x;
        this.y = y;
        this.c = c;
        this.set = set;
        this.select = select;
    }
}
class Point {
    int x, y;
    Point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}
class Solution {
    static final int[] dx = {-1, 0, 1, 0};
    static final int[] dy = {0, -1, 0, 1};
    static boolean[][][] visited;
    static int max_set = 0;
    static int answer = 0;
    public int solution(int[][] board, int r, int c) {
        for(int i=0; i<=15; i++) max_set = max_set | (1 << i);
        visited = new boolean[4][4][max_set + 1];
        Node start = new Node(c, r, 0, 0, -1); //-1 -> 선택하지 않음.
        for(int i=0; i<board.length; i++) {
            for(int j=0; j<board[i].length; j++) {
                if(board[i][j] == 0) start.set = start.set | (1 << conversion_point(j, i));
            }
        }
        BFS(start, board);
        return answer;
    }
    
    static void BFS(Node start, int[][] board) {
        Queue<Node> que = new LinkedList<>();
        que.add(start);
        visited[start.y][start.x][start.set] = true;
        while(que.size() != 0) {
            Node n = que.poll();
            if(n.set == max_set) {
                answer = n.c;
                break;
            }
            //enter 연산
            int next_set = n.set | (1 << conversion_point(n.x, n.y));
            if(board[n.y][n.x] != 0 && n.set != next_set) {
                if(n.select == -1) {
                    //아직 선택한 카드가 없을 때.
                    if(!visited[n.y][n.x][next_set]) {
                        que.add(new Node(n.x, n.y, n.c + 1, next_set, board[n.y][n.x]));
                        visited[n.y][n.x][next_set] = true;
                    }
                } else {
                    //선택한 카드가 있을 때
                    if(!visited[n.y][n.x][next_set] && n.select == board[n.y][n.x]) {
                        //카드의 값이 같을 때
                        que.add(new Node(n.x, n.y, n.c + 1, next_set, -1));
                        visited[n.y][n.x][next_set] = true;
                    }
                }
            }
            //이동 연산
            //기본 이동 연산
            for(int i=0; i<4; i++) {
                int nx = n.x + dx[i];
                int ny = n.y + dy[i];
                if((0 <= nx && nx <= 3) && (0 <= ny && ny <= 3)) {
                    if(!visited[ny][nx][n.set]) {
                        que.add(new Node(nx, ny, n.c + 1, n.set, n.select));
                        visited[ny][nx][n.set] = true;
                    }
                }
            }
            //ctrl 이동 연산
            for(int i=0; i<4; i++) {
                Point next_p = ctrl_move(new Point(n.x, n.y), i, n.set, board);
                if(!visited[next_p.y][next_p.x][n.set]) {
                    que.add(new Node(next_p.x, next_p.y, n.c + 1, n.set, n.select));
                    visited[next_p.y][next_p.x][n.set] = true;
                }
            }
        }
    }
    
    static Point ctrl_move(Point p, int dir, int set,int[][] board) {
        while(true) {
            int nx = p.x + dx[dir];
            int ny = p.y + dy[dir];
            if((0<= nx && nx <= 3) && (0 <= ny && ny <= 3)) {
                if(board[ny][nx] != 0) {
                    int next_set = set | (1 << conversion_point(nx, ny));
                    if(set != next_set) {
                        //카드가 존재할 때
                        return new Point(nx, ny);
                    }    
                }
            } else return new Point(p.x, p.y);
            p = new Point(nx, ny);
        }
    }
    
    static int conversion_point(int x, int y) {
        return y * 4 + x;
    }
}