[프로그래머스] 합승 택시 요금 - Java

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/72413

문제

링크 참조

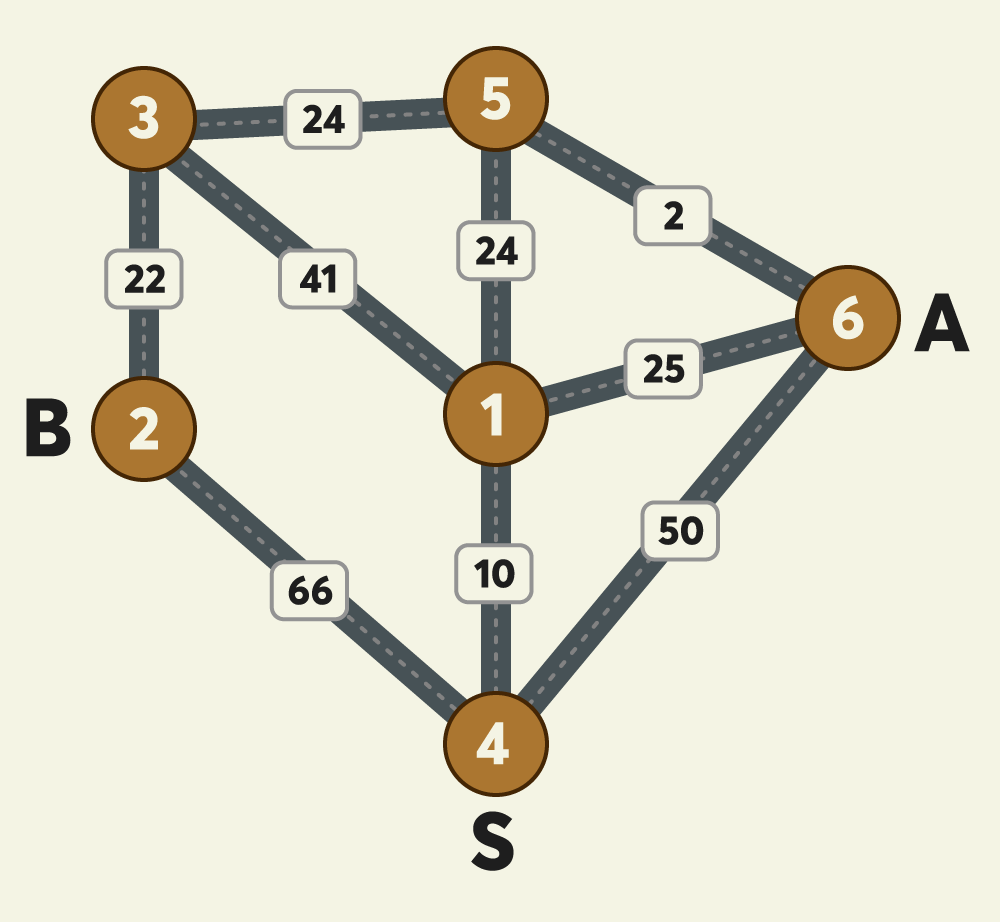
제한사항

링크 참조

알고리즘: 데익스트라

풀이

전형적인 데익스트라 문제다.
문제의 목표는 두 사람이 모두 귀가하는 데 소요되는 최저 택시요금을 계산해야 한다.
처음 S에서 A, B 두 사람이 출발하기 때문에 S에서 각 지점까지 최소 거리를 구한다. 이때 데익스트라를 이용한다. S에서 C까지 이동했다는 뜻은 C까지 합승했다는 의미다. 즉 말로 풀어보면 (S부터 C까지 최소 거리 + C부터 A까지 최소 거리 + C부터 B까지 최소 거리) 값 중 최솟값을 구하면 된다. S에서 C까지 최소 거리는 구했고,
이제 각 지점에서 모든 지점까지의 최소 거리를 구하면 된다. -> 이때도 데익스트라를 이용한다.

전체 시간 복잡도를 계산해 보면 데익스트라의 시간 복잡도는 O((V+E) logE)고, 총 200번 반복하기 때문에 O(200 (V+E) * logE)다. 그래서 위 풀이로 충분히 효율성 체크를 통과할 수 있다.

소스 코드

import java.util.*;
class Node implements Comparable<Node>{
    int p, w;
    Node(int p, int w) {
        this.p = p;
        this.w = w;
    }
    public int compareTo(Node o) {
        return this.w - o.w;
    }
}
class Solution {
    static ArrayList<ArrayList<Node>> graph = new ArrayList<>();
    static int N;
    public int solution(int n, int s, int a, int b, int[][] fares) {
        int answer = Integer.MAX_VALUE;
        N = n;
        for(int i=0; i<=n; i++) graph.add(new ArrayList<>());
        for(int i=0; i<fares.length; i++) {
            int p1 = fares[i][0];
            int p2 = fares[i][1];
            int w = fares[i][2];
            graph.get(p1).add(new Node(p2, w));
            graph.get(p2).add(new Node(p1, w));
        }
        int[] c_dp = dijkstra(s);
        for(int i=1; i<=n; i++) {
            if(c_dp[i] != Integer.MAX_VALUE) {
                int[] ab_dp = dijkstra(i);
                answer = Math.min(answer, c_dp[i] + ab_dp[a] + ab_dp[b]);
            }
        }
        return answer;
    }

    static int[] dijkstra(int start) {
        int[] dp = new int[N+1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        boolean[] visited = new boolean[N+1];
        PriorityQueue<Node> pq = new PriorityQueue<>();
        dp[start] = 0; //시작점
        pq.offer(new Node(start, 0));
        while(!pq.isEmpty()) {
            Node n = pq.poll();
            if(visited[n.p]) continue; //이미 방문했다면
            visited[n.p] = true;
            for(int i=0; i<graph.get(n.p).size(); i++) {
                int next_p = graph.get(n.p).get(i).p;
                int next_w = n.w + graph.get(n.p).get(i).w;
                if(dp[next_p] > next_w) {
                    dp[next_p] = next_w;
                    pq.offer(new Node(next_p, next_w));
                }
            }
        }
        return dp;
    }
}