문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/42890
문제 설명
후보키
프렌즈대학교 컴퓨터공학과 조교인 제이지는 네오 학과장님의 지시로, 학생들의 인적사항을 정리하는 업무를 담당하게 되었다.
그의 학부 시절 프로그래밍 경험을 되살려, 모든 인적사항을 데이터베이스에 넣기로 하였고, 이를 위해 정리를 하던 중에 후보키(Candidate Key)에 대한 고민이 필요하게 되었다.
후보 키에 대한 내용이 잘 기억나지 않던 제이지는, 정확한 내용을 파악하기 위해 데이터베이스 관련 서적을 확인하여 아래와 같은 내용을 확인하였다.
- 관계 데이터베이스에서 릴레이션(Relation)의 튜플(Tuple)을 유일하게 식별할 수 있는 속성(Attribute) 또는 속성의 집합 중, 다음 두 성질을 만족하는 것을 후보 키(Candidate Key)라고 한다.
- 유일성(uniqueness) : 릴레이션에 있는 모든 튜플에 대해 유일하게 식별되어야 한다.
- 최소성(minimality) : 유일성을 가진 키를 구성하는 속성(Attribute) 중 하나라도 제외하는 경우 유일성이 깨지는 것을 의미한다. 즉, 릴레이션의 모든 튜플을 유일하게 식별하는 데 꼭 필요한 속성들로만 구성되어야 한다.
제이지를 위해, 아래와 같은 학생들의 인적사항이 주어졌을 때, 후보 키의 최대 개수를 구하라.
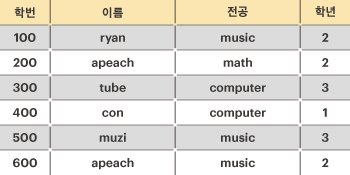
위의 예를 설명하면, 학생의 인적사항 릴레이션에서 모든 학생은 각자 유일한 "학번"을 가지고 있다. 따라서 "학번"은 릴레이션의 후보 키가 될 수 있다.
그다음 "이름"에 대해서는 같은 이름("apeach")을 사용하는 학생이 있기 때문에, "이름"은 후보 키가 될 수 없다. 그러나, 만약 ["이름", "전공"]을 함께 사용한다면 릴레이션의 모든 튜플을 유일하게 식별 가능하므로 후보 키가 될 수 있게 된다.
물론 ["이름", "전공", "학년"]을 함께 사용해도 릴레이션의 모든 튜플을 유일하게 식별할 수 있지만, 최소성을 만족하지 못하기 때문에 후보 키가 될 수 없다.
따라서, 위의 학생 인적사항의 후보 키는 "학번", ["이름", "전공"] 두 개가 된다.
릴레이션을 나타내는 문자열 배열 relation이 매개변수로 주어질 때, 이 릴레이션에서 후보 키의 개수를 return 하도록 solution 함수를 완성하라.
제한사항
- relation은 2차원 문자열 배열이다.
- relation의 컬럼(column)의 길이는 1 이상 8 이하이며, 각각의 컬럼은 릴레이션의 속성을 나타낸다.
- relation의 로우(row)의 길이는 1 이상 20 이하이며, 각각의 로우는 릴레이션의 튜플을 나타낸다.
- relation의 모든 문자열의 길이는 1 이상 8 이하이며, 알파벳 소문자와 숫자로만 이루어져 있다.
- relation의 모든 튜플은 유일하게 식별 가능하다.(즉, 중복되는 튜플은 없다.)
알고리즘: 집합, 구현, 조합
풀이
이 문제는 후보 키의 개수를 출력하는 문제다.
후보 키란 문제에서 정의하듯이 유일성과 최소성을 만족해야 한다.
즉 후보 키를 이루는 속성 집합은 다른 후보키를 포함해서는 안된다.
위 예시를 볼 때 ["이름", "전공", "학년"]이 key는 후보키인 ["이름", "전공"]을 포함하기 때문에 후보키라고 할 수 없는 것이다.
이제 위 사실을 알았다면, 모든 속성 조합을 뽑는다. (컬럼이 4라면 1개로 이루어진, 2개로 이루어진, 3개로 이루어진, 4개로 이루어진 모든 속성 조합을 뽑음)
그러한 경우의 수는 최대 8C1 + 8C2 + 8C3 ... 8C8이기 때문에 총 255개 존재한다.
그리고 각 조합마다 후보 키가 가능한지 판단하는데
최소성은 후보 키 list를 돌면서 현재 조합에 후보 키가 포함돼 있는지 검사하면 된다. (HashSet 이용) 주의할점은 적게 뽑는 순으로 후보 키 list를 먼저 구성해야 한다.
ex) 하나를 뽑는 경우 -> 두 개를 뽑는 경우 -> ....
유일성은 relation을 돌면서 중복되는 tuple이 없는지 검사하면 된다. (String 이용) 주의할 점은 컬럼 사이를 ,나 공백으로 구분해 줘야 한다.
구분해 주지 않으면 10110은 10 110, 101 10을 구분할 수 없기 때문이다.
시간 복잡도를 계산하면 모든 조합 255 후보 키 list 약 255 릴레아션 검사 약 400으로 26,010,000이다. (worst case)
소스 코드
import java.util.*;
class Solution {
static HashSet<Integer> result = new HashSet<>();
static ArrayList<HashSet<Integer>> cd_key_list = new ArrayList<>();
static int answer = 0;
public int solution(String[][] relation) {
for(int i=1; i<=relation[0].length; i++) {
DFS(i, relation, 0);
}
return answer;
}
static void DFS(int depth, String[][] relation, int ind) {
if(result.size() == depth) {
if(included_set()) {
if(isCdKey(relation)) {
HashSet<Integer> set = new HashSet<>();
set.addAll(result);
cd_key_list.add(set);
answer += 1;
}
}
return;
}
for(int i=ind; i<relation[0].length; i++) {
result.add(i);
DFS(depth, relation, i + 1);
result.remove(i);
}
}
static boolean isCdKey(String[][] relation) {
ArrayList<String> tuple_list = new ArrayList<>();
for(int i=0; i<relation.length; i++) {
StringBuilder tuple = new StringBuilder();
Iterator<Integer> it = result.iterator();
while(it.hasNext()) tuple.append(relation[i][it.next()] + " ");
//check
for(int j=0; j<tuple_list.size(); j++) {
if(tuple.toString().trim().equals(tuple_list.get(j))) return false;
}
tuple_list.add(tuple.toString().trim());
}
return true;
}
static boolean included_set() {
for(int i=0; i<cd_key_list.size(); i++) {
if(result.containsAll(cd_key_list.get(i))) return false;
}
return true;
}
}