Tensor and Tensor decompositions
1. Tensor
1.1. Definition
- An array containing multidimentional elements.
- N-order or N-way or N-mode tensor is an element of the tensor product of N vector spaces.
1.2. Examples
- A first order tensor is a vector, and a second order tensor is a matrix.
- A Third order tensor is
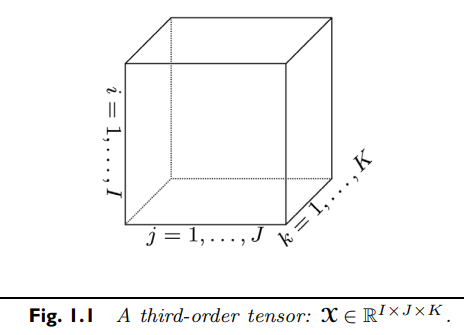 Each index is an element of I vector space, J vector space, K vector space.
Each index is an element of I vector space, J vector space, K vector space.
2. Notations
- The order of a tensor : The number of dimensions a.k.a. ways, mods
- Vectors : Boldface lowercase letters, e.g., a
- The ith element of a vector a is ai.
- Metrices : Boldface capital letters, e.g., A
- An element (i,j) of a matrix A is aij.
- Tensors : Boldface LaTex letters, e.g., X
- An element (i,j,k) of a tensor X is denoted by xijk.
- The nth element of a sequence is denoted by a superscript in parentheses.
e.g. A(n): nth matrix in a sequence
- Fibers : Fixing every index but one
e.g. A matrix column : mode-1 fiber
A matrix row : mode-2 fiber
For a 3-order tensor: 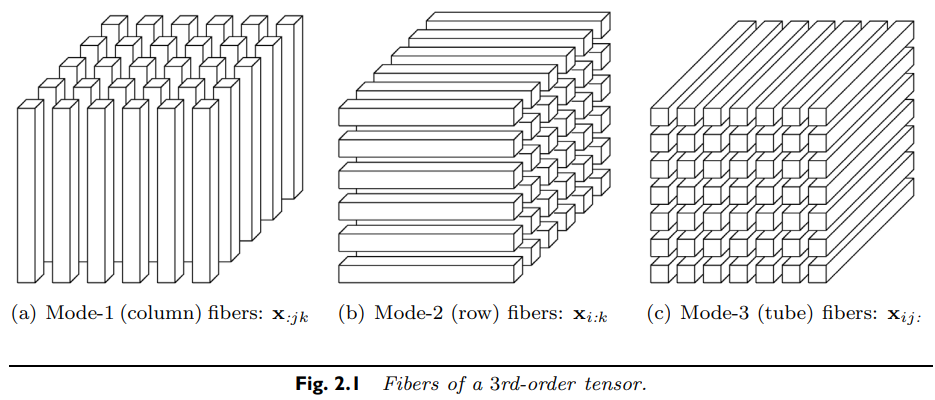
- Slices : Fixing all but two indices, two-dimentional sections of a tensor.
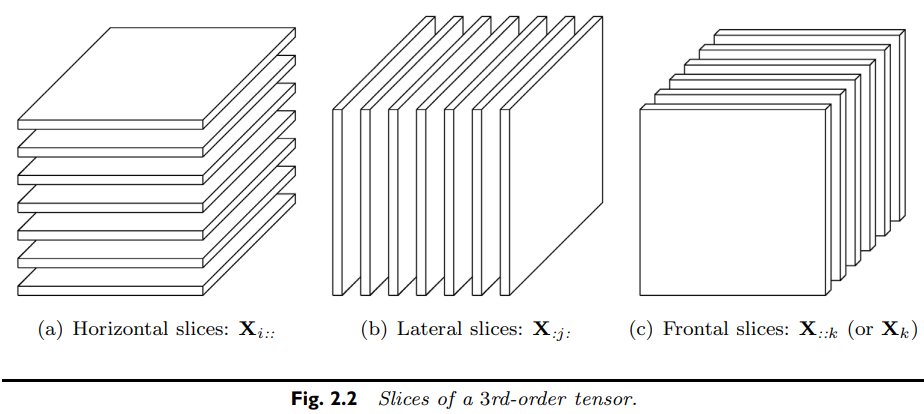
- Norm : The norm of a tensor X∈RI1×I2×⋯×IN ,
denoted by ∥X∥=i1=1∑I1i2=1∑I2⋯in=1∑INxi1i2⋯iN2
- a.k.a unfolding or flattening, is reordering elements of an N-way Tensor into a matrix.
- The mode-n matricization of a tensor X∈RI1×I2×⋯×IN is denoted by X(n) and arranges the mode-n fibers to be the columns of the resulting matrix.
- Tensor element (i1,i2,…,iN) maps to matrix element (in,j), where
j=1+k=1k=n∑N(ik−1)Jk with Jk=m=1m=n∏k−1Im
Describing mode-n fibers being the columns of the resulting matrix.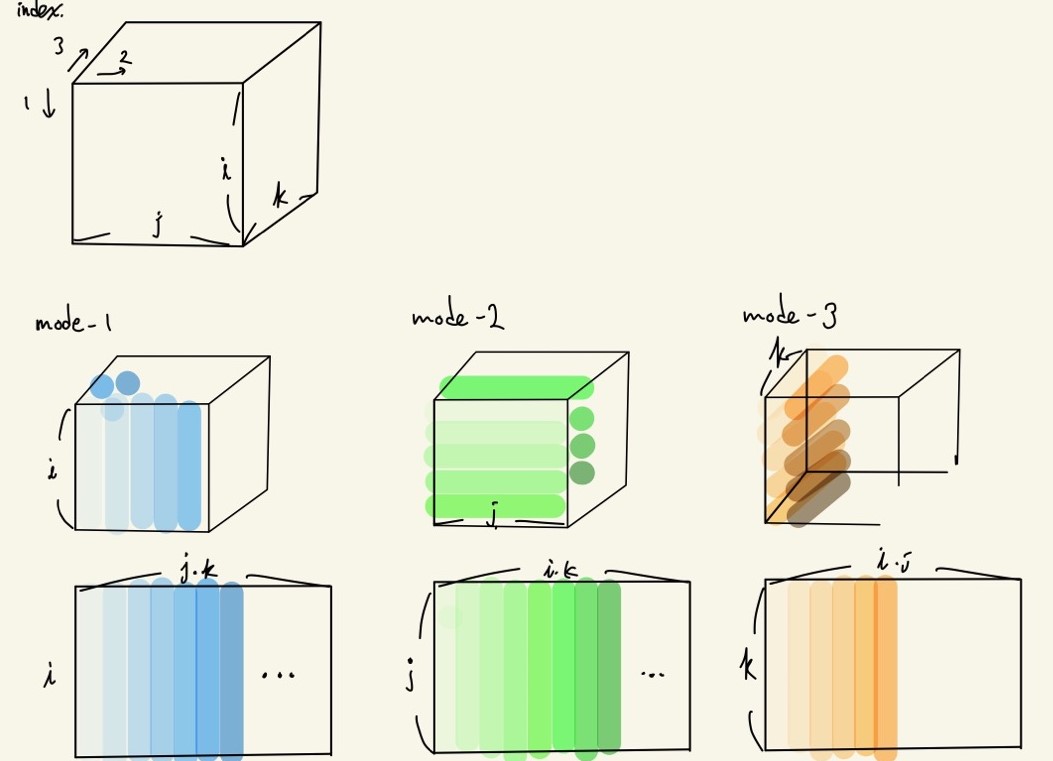
Each index is an element of vector space, vector space, vector space.



