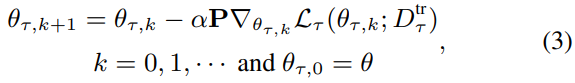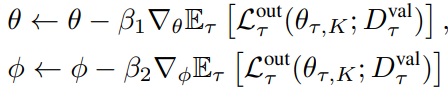1. Introduction

• MAML, one of the most popular optimization based meta-learning algorithm.
• Preconditioned MAML
  - Imporved by Preconditioned Gradient Descent(PGD) for inner loop optimization
  - Meta learns not only initialization parameters of models but also meta-parameters of preconditioner $P$.
  - $P$ was adapted with innder-step k or with individual task separately, thus Riemman metric condition cannot be satisfied.
  • Riemman metric : A condition that the steepest gradient descent can be achieved on a given parameter space.
• Proposing Geometry Adaptive Preconditioned gradient descent (GAP), which includes two unconsidered properties.
  -$P_{GAP}$ is adapted with individual task and optimization path(path dependent i,e, innder-step dependent).
  -$P_{GAP}$ is a Riemman metric.

2. Background

2.1. MAML

Inner loop

Outer loop

        Note that, $\Sigma_{\tau\sim P(\tau)}L_\tau$ has used instead of $E_{\tau}[L_{\tau}^{out}]$, on the MAML paper.

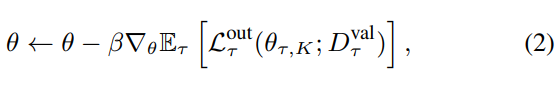
2.2. PGD

Preconditioned gradient update

       $\bullet$ PGD often reduces the effect of pathological curvature and speed up the optimization.

2.3. Unfolding: reshaping a tensor into a matrix

       Tensor and Tensor decompositions link

2.4. Riemmannian manifold

       Riemannian manifold and metric

3. Methodology

Setting

• $L$ : number of layers of NN
• $\theta = \{\mathsf{W}^1,\cdots,\mathsf{W}^l,\cdots,\mathsf{W}^L\}$ : CNN parameters
• $\phi = \{\mathbf{M}^1,\cdots,\mathbf{M}^l,\cdots,\mathbf{M}^L\}$ : preconditioner parameters
• $\mathcal{T}_i\sim p(\mathcal{D})$, $\mathcal{T}_i$ : batch of tasks
• $\tau\in \mathcal{T}_i$ , $\tau$ : a task
• $K$ : number of samples

3.1. GAP: Geometry-Adaptive Preconditioner

3.1.1 Inner-Loop Optimization

• L-layer neural network $f_\theta(\cdot)$ with parameters $\theta =\{$W$^1,\cdots,$W$^l,\cdots,$W$^L\}$

• Let gradient G$_{\tau,k}^l=\nabla$W$_{\tau,k}^l L_{\tau}^{in}(\theta_{\tau,k};D^{tr})$

• Reshape G$_{\tau,k}^l$ witn unfolding mode-1 into $G_{\tau,k}^l$. (mode-1 performs the best)

• Define additional parameters $\phi = \{M^l\}_{l=1}^L$ where $m_i^l \in R, \; Sp(x)=\frac{1}{2}log(1+exp(2*x))$

• SVD $G_{\tau,k}^l$ into $U_{\tau,k}^l\Sigma_{\tau,k}^l(V_{\tau,k}^l)^T,$
  and $\widetilde{G}_{\tau,k}^l = U_{\tau,k}^l(M_{\tau,k}^l\Sigma_{\tau,k}^l)(V_{\tau,k}^l)^T$

• Reshape $\widetilde{G}_{\tau,k}^l$ back to it's original tensor form

• Preconditioned gradient descent of GAP becomes:

3.1.2 Outer-loop Optimization

• GAP learns two parameter sets $\theta,\phi :$

3.1.3 Training precedure

3.1.4 Desirable properties of GAP

• 1. Fully adaptive in both task-specific($\tau$) and path-depend($k$) way
• 2. Riemannian metric
  • Steepest descent learning