⏱ 시간 복잡도
시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 가리킨다. - 출처
시간 복잡도는 한마디로, 내가 짠 코드가 얼마나 효율적인지, 코드의 실행 시간을 예측한 개념입니다. 이 실행 시간은 코드의 연산이 많아질 수록 증가합니다.
단순한 덧셈, 뺄셈 등 기본적인 연산 외에, 개발자라는 직함을 갖고 일하기 위해선 코드가 잘 작동하는 것은 기본이고, 이 코드를 얼마나 효율적으로 짤 수 있는지 항상 고민해야 합니다.
시간 복잡도는 통상적으로 빅 오 표기법(Big O)으로 표현합니다. 입력으로 들어온 데이터의 증가율에 따른 알고리즘 성능을 예측하는 데 사용됩니다.
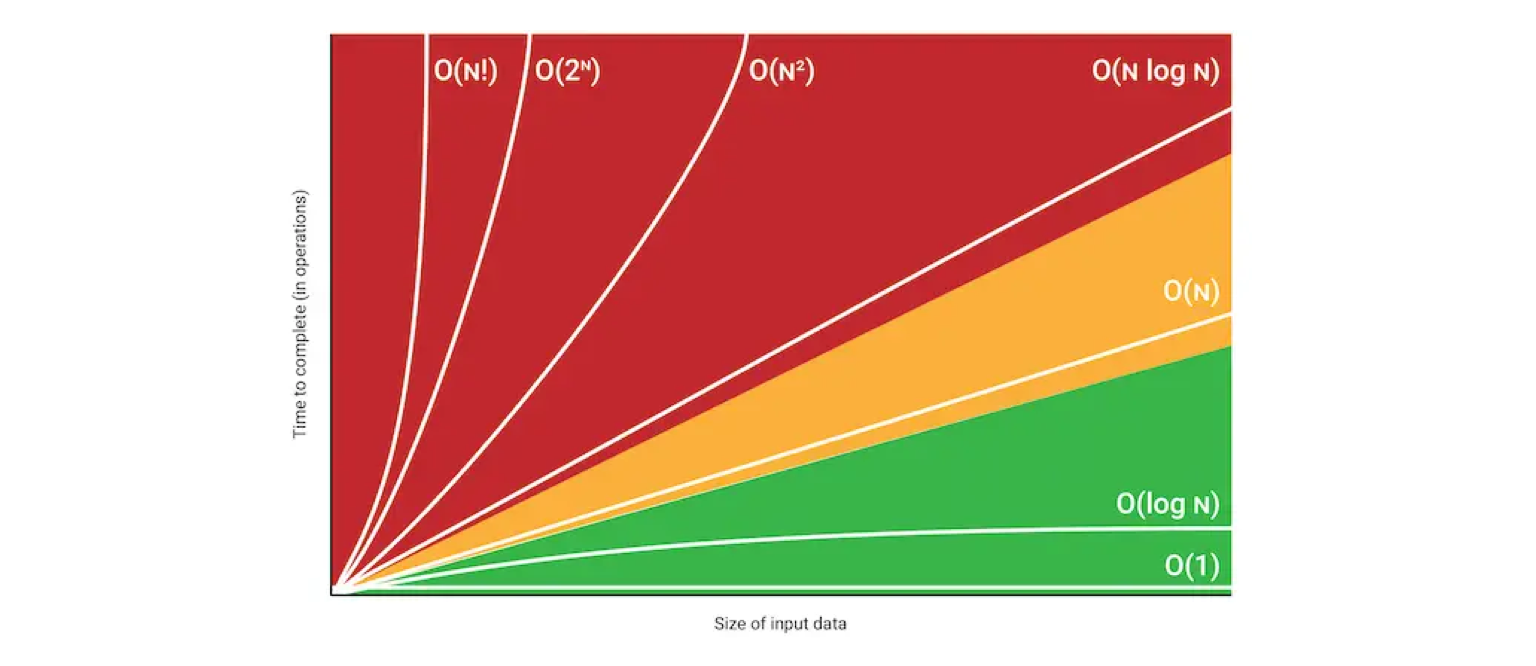
위 도표는 입력 데이터의 크기의 증가에 따른 알고리즘 구현 시간을 시각화한 자료입니다.
입력 데이터의 크기가 늘어날 수록 시간이 기하 급수로 증가하는 그래프가 있는가 하면, 완만하거나 아예 변화가 없는 그래프가 있습니다.
빅 오 표기법으로 표기된 알고리즘의 시간 복잡도에 대한 상세 설명은 아래 링크에서 더 확인하실 수 있습니다.
시간 복잡도를 고려하지 않은 피보나치 수열
- O(2ⁿ) (Exponential)
데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘이다. 대표적으로 피보나치 수열이 있으며, 재귀가 역기능을 할 경우도 해당된다.
우리는 반복문, 또는 재귀를 이용하여 피보나치 수열을 구현할 수 있습니다.
// 재귀를 이용한 피보나치 수열
let fibonacci = function (n) {
let base = [0, 1];
if(n < 2) {
return n
}
return fibonacci(n - 2) + fibonacci(n - 1);
}// 반복문을 이용한 피보나치 수열
function fibonacci(num) {
let result = [0,1]
if (num ===0){
return [0]
}
if (num ===1){
return [0,1]
}
let getFiboNum;
for(let i = 3; i <= num; i++){
getFiboNum = result[i-2] + result[i-1];
result.push(getFiboNum)
}
return result
}위와 같이 재귀와 반복문을 이용해 원하는 피보나치 수열의 자릿수를 알 수 있습니다.
그러나, 처리해야할 데이터가 많아진다면? 예를 들어 피보나치 수열의 50번째 값을 알기 위해 우리는 이미 그 이전의 수를 알고있어도 같은 작업 getFiboNum = result[i-2] + result[i-1]; 를 반복해야합니다.
수열의 50번째 값을 알기 위해, 49, 48번째 값을 알아야하고, 49, 48번째 값을 모르기 때문에 계산을 또 반복하고... 컴퓨터는 무한 츠쿠요미에 걸려버립니다...
시간 복잡도를 개선한 피보나치 수열
처리해야할 데이터량이 많아, 처리 시간이 급격하게 늘어나는 것을 방지하기 위해 선배 개발자님들은 불철주야 고민하십니다. 이 비효율적인 피보나치 수열을 구하는 함수의 시간 복잡도를 개선하는 방법이 무엇일까요?
했던 계산은 메모해두고, 또 안하면 될 것 같습니다!
이를 동적 계획법 또는 Dynamic with memoization 기법으로 구현할 수 있습니다.
이미 해결한 문제의 정답을 따로 기록해두고, 다시 해결하지 않는 기법입니다.
let fibonacci = function (n) {
let memo = [0, 1];
let aux = function(n) {
if(memo[n] !== undefined){
return memo[n] // 피보나치 배열 memo에 입력한 숫자의 값이 존재한다면 반환합니다.
}
else { // 존재하지 않다면, 피보나치 계산을 수행하여 그 값을 memo에 추가합니다.
memo[n] = aux(n - 2) + aux(n - 1);
return memo[n]
}
}
return aux(n)
}위와 같이, 이미 수행했던 연산을 피보나치 배열에 메모해두고, 해당 값을 배열에서 호출하는 것으로 수행했던 연산을 재수행하지 않습니다. 이 때 시간복잡도는 한번 연산했던 값은 연산으로 구하지 않으므로 O(N)이 됩니다.
틀린 부분이 있다면 적극 피드백 주시길 바라며, 이만 글 줄이겠습니다! 긴 글 읽어주셔서 감사드립니다. 🙇

