Auto Filmer: Autonomous Aerial Videography Under Human Interaction 논문 리뷰

신희준·2024년 12월 7일

Paper Review

목록 보기

30/30

Paper : Auto Filmer: Autonomous Aerial Videography Under Human Interaction (Zhiwei Zhang; Yuhang Zhong; Junlong Guo; Qianhao Wang; Chao Xu; Fei Gao / IEEE RAL 2023)

code: https://github.com/ZJU-FAST-Lab/Auto-Filmer/tree/main?tab=readme-ov-file

video : https://www.youtube.com/watch?v=Lrk9MVJEMpo

Highlights

Customized shot (shooting rules)과 drone dynamics (motion)를 결합한 자율 비행 interactive videography system 제시 → Real-time으로 원하는 촬영 구도를 설정할 수 있음
Shooting demands를 만족하면서 충돌과 가려짐이 없는 초기 경로를 찾는 front-end process
Stable video frame을 가능케하도록 drone과 gimbal을 동시에 최적화

→ 기존의 trajectory planning 연구에서 shot constraint를 추가한 것이 핵심

Introduction

Aerial videography는 cinematography 등 여러 분야에서 사용되지만, 실제로 uav를 통해 대상을 촬영하는 것은 매우 어려움 → 예를 들어 조종기로 조작 시에 움직임은 linear하지만 circular motion 등은 실제로 non-linear trajectory를 구현해야 함 → 짐벌을 같이 조종하는 것은 더 어려운 일. → 동시에 대상까지 추적해야 한다.

최근에는 여러 vision recognition 연구와 motion planning 연구를 통해서 UAV가 자동으로 따라다니면서 촬영하는 시도가 많이 있었지만, 아직 촬영의 미적인 요소나 human interaction을 고려한 연구는 많이 없음 (Elastic-Tracker 등의 aerial tracker도 매우 성능이 좋긴 함)
이러한 사람들의 촬영 요소에 대한 요구를 robot motion으로 반영하는 것이 어려운 일
- robot의 움직임에는 여러 공간적 제약이 존재 (장애물, 가려짐 등)
- robot의 motion 자체로 인해 촬영 구도가 변할 수 있음 (image 에서 보이는 타겟의 위치 등)
해당 연구인 Auto Filmer은 촬영자의 촬영 조건 등을 실시간으로 고려하여 robot trajectory planning을 수행하는 interative videography system
이 trajectory planning은 hierarchical planning scheme을 가짐
- front-end process
  - robot의 initial path를 생성하기 위한 몇 개의 점들을 추출
  - Initial path 주변으로 드론이 위치해야하는 region을 정의 → 이 region은 videography requirements를 만족하면서 drone의 safety와 target에 대한 visibility를 고려한 region
- back-end trajectory optimization
  - 위에서 생성한 potential region을 바탕으로 최적의 trajectory 생성

Prerequisites

Videography Interaction

videography에서 중요한 세 가지 factors
- shot length
- perspective
- image composition (촬영 화면 안에서 물체들의 layout과 관련된 것들)
- + transition time (얼마나 빠르게 한 촬영 패턴에서 다른 촬영 패턴으로 넘어가는지)
이러한 videography 요소들을 수학식으로 표현하기 위해서 아래의 parameter들이 필요

이미지 상에서 물체의 위치와 속도

P_{img}=\begin{bmatrix} U_{img} \\ V_{img} \end{bmatrix}, \dot{P}_{img}

드론과 타겟의 상대적인 각도 $\mathcal{\Theta}$
카메라와 타겟의 거리 $\mathcal{D}$
Transition Time $\mathcal{T}$

→ 이는 아래의 GUI처럼 표현할 수 있음

해당 방법론의 계획 단계에서, 위의 videography parameter $\mathcal{S}=\{P_{img}, \dot{P}_{img}, \Theta, \mathcal{D} \}$ 는 매 time stamp마다 할당되는 값 → 이 파라미터들이 촬영 모드를 정의한다고 볼 수 있을 듯

특히 이 과정은 두 단계로 나뉨
1. Stable stage : 드론이 타겟을 고정된 패턴을 유지하면서 타겟을 촬영
  
  → $P_{img}, \theta, \mathcal{D}$ 는 constant, $\dot{P}_{img}$ 는 0을 가짐
2. Transition state : 이전 촬영 configuration에서 새로 지정된 config로 촬영 frame이 변화하는 과정.
  
  → 이 state에서 parameter들은 시간에 따라 interpolate됨
  
  → $\dot{P}_{img}$ 는 constant

Hardware

Videography platform은 같은 연구실의 FAST-TRACKER를 따랐다고 한다.
자율주행 videography 시스템에서 visual perception은 두 가지 중요한 역할을 수행
- Environment sensing : 장애물 회피 등을 위해 mapping하는 역할
- Target tracking : 타겟을 추적하는 역할
해당 연구에서는 mapping을 위한 depth camera와 촬영을 위한 monocular camera를 따로 사용했다고 한다.

또한 짐벌은 yaw방향 회전을 하는 것을 사용

 → 구현해놓은 것 보면 드론의 heading은 velocity방향이고, 실제로 타겟을 tracking하는 것은 짐벌의 몫. (Depth camera가 앞을 바라보고 있어야 mapping하면서 장애물 회피 가능하므로)

안정적인 frame을 담기 위해 gimbal motion도 함께 계획

Front-End Process

제안된 framework의 front-end 파트는 trajectory optimization에 필요한 여러 조건들을 설계한다.
- Videography 조건을 만족하면서 Kinodynamic constraints를 만족하는 path를 탐색 (collision-free motions with dynamic limits)
- 타겟의 visibility를 보장하기 위해, initial path를 따라 view regions를 생성
- 드론의 안전성을 보장하기 위해 safe flight corridors 생성

Kinodynamic Path Searching

Hybrid A* path search 알고리즘을 사용
각 node는 robot state를 represent하며, A star와 비슷하게 각 node에는 출발지부터 현재까지의 effort인 cost function $g(n)$ 과 도착지까지 effort estimate인 heuristic function $h(n)$ 이 할당됌
하지만 목적지까지 가장 짧은 경로를 찾는 대신, 해당 연구의 videography kinodynamic search는 주어진 videography parameter와 차이를 가장 적게하는 경로를 찾음
- safe & occlusion-free path
- 즉, videography parameter를 만족하도록 하는 drone state를 goal point로 여기고 최적의 path를 찾는다고 이해하자.
여기서 planner는 target motion의 미래 information을 필요로 한다.
이때 target의 motion을 예측하는 prediction module이 필요한데, 이는 motion model을 활용한 kalman filter를 활용하든, deep learning model을 활용하면 될 것 같다.

→ 이 논문의 scope는 아님.

어쨋든 prediction module은 아래의 정보를 줄 수 있어야 한다.
- target의 predicted position $\{ {\xi}_n \in \mathbb{R}^3, t_n \},\; n=0,1,...,N \;, 0 <t_n \le T_{pre}$
- target의 predicted velocity $\{ \dot{\xi}_n \in \mathbb{R}^3, t_n \}, \; n=0,1,...,N \;, 0 <t_n \le T_{pre}$
- $N$ 은 prediction points, $T_{pre}$ 는 horizon (→ 즉 현재로부터 앞으로 정해진 time 동안 예측)
경로 탐색을 하는 동안, node들은 이 prediction과 같은 시간 간격으로 확장되어간다.

→ 그러므로 각 노드 $n$ 에 대해 현 시간 $t_n$ 에서 드론의 state뿐만 아니라 target의 위치 $\xi_n$ 이 필요하다.

그러면 현재 드론의 position으로부터 target을 가르키는 벡터를 아래와 같이 정의할 수 있다.

r=[r_x,r_y,r_z]^T=\xi_n-p_n

그리고 관련된 videography factor들은 아래와 같이 계산된다. ( $\phi$ 는 타겟을 볼 때의 tilt angle)

d_n=||r|| \\ \theta_n=atan2(r_y,r_x) \\ \phi_n=arctan \frac{r_z}{r_x^2+r_y^2}

위의 값들을 Prerequisites에서 언급했던 videography parameter들이 각 time $t_n$ 마다 할당되어 있으므로, 각 node의 cost function은 user-assigned shooting parameter와의 차이로 정의할 수 있다.

g(n)=\lambda_d(D_n-d_n)^2+\lambda_\theta(\Theta_n-\theta_n)+\lambda_\Phi(\Phi_n-\phi_n)

$\lambda$ 는 cost weights
여기서 desired tilt angle $\Phi$ 는 아래와 같이 구해줄 수 있다. ( $C, F$ 는 camera intrinsic)

\Phi_n=arctan\frac{\mathcal{V}^n_{img}-C_y}{F_y}

Search process는 graph가 target prediction $T_{pre}$ 에 도달하면 종료.
Heuristic function은 searching을 빠르게 하기 위해서 시간 차로 설정

h(n)=T_{pre}-t_n

또한, 이 연구에서는 velocity control input을 사용하는데, primitives $\{ u_{max}, 0, -u_{max} \}$ 값을 활용하여 각 $x,y,z$ 방향으로 확장 가능한 노드들을 선별 (예를 들어, $x$ 방향으로 최고 속도 $u_{max}$ , 나머지 방향 y, z로는 0 velocity를 가지는 경우가 한 노드라고 생각) → 즉, 한번의 node expansion에 $3 \times 3\times 3=27$ 가지의 새 node (state)들을 고려 → 물론 장애물 등을 고려해서 불가능한 state는 제외

View Region Selection

Kinodynamic search를 통해 얻은 경로 (waypoint)는 아직 optimal solution을 제공하지는 못함 → visibility를 보장하기 위해 view region이라는 영역을 추출

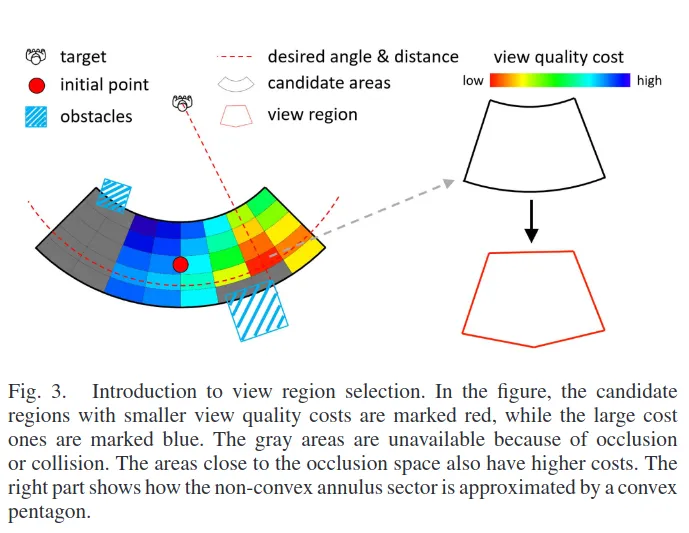
View Region을 생성하기 위해서 다음의 작업이 수행된다. (위 그림 참조)
먼저, 드론의 dynamic limit을 기반으로 각 time $t_n$ 에서 initial point로부터 adjustable한 영역을 추출한다.
Videography 특성상 video quality는 distance와 perspective의 영향을 크게 받으므로, voxel이 아닌 고리 형태로 이 영역을 여러 후보로 잘게 나눈다. (예를 들어 후보 영역 중 빨간색 영역은 그림에서 보다시피 특정 거리와 각도를 포함하는 영역)
각 영역은 타겟에 상대적으로 특정 거리와 각도를 가지게 되는데, 이 값들의 medium 값을 기반으로 아래의 evaluation 함수 $Q_i$ 를 계산할 수 있다.

Q_i=\lambda_d ||D_n-d_i|| + \lambda_\theta ||\Theta_n-\theta_i||+ \lambda_{occ} min_j||\theta^j_{occ}-\theta_i||

여기서 마지막 term이 장애물에 가려지는 것에 대한 visibility를 측정해주며, occlusion angle $\theta^j_{occ}$ 는 ray-casting을 통해 정해질 수 있는 각
장애물 등에 의해서 가려지는 영역은 후보는 제외하고, 최소의 $Q_i$ 를 갖는 후보 area가 view region으로 선택된다.
선택된 view region은 이후 최적화를 위해 convex area로 approximate된다.
이 연구에서는 이를 polytope로 표현

\mathcal{V}=\{ p \in \mathbb{R}^3 | A_v \cdot p - b_v \le 0\}

Corridor Construction

View region은 특정 prediction time에서 촬영 위치를 결정하지만, 전체적인 경로의 safety가 보장되지는 않음 → Elastic-Tracker의 safe flight corridor construction 방법을 사용 (추후 요 논문도 정리하려고 함)
A*를 이용해 각 view region의 center를 연결하고, 이를 바탕으로 obstacle-free한 polyhedron을 생성한다. (아래 그림과 같은 식이라고 보면 될 것 같다.)

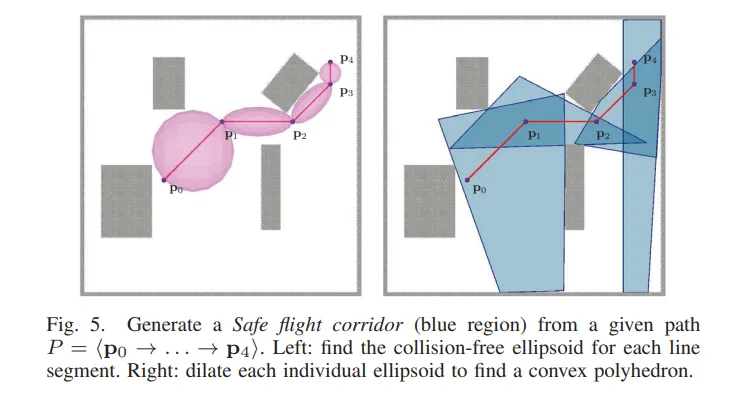
출처: Planning Dynamically Feasible Trajectories for Quadrotors Using Safe Flight Corridors in 3-D Complex Environments

이러한 flight corridor는 polyhedra로 표현

\mathcal{F}=\{p \in \mathbb {R}^3 | A_f \cdot p - b_f \le 0 \}

Trajectory Optimization

Trajectory Representation

이 연구에서는 MINCO trajectory class를 활용하여 드론의 trajectory를 표현하고 최적화한다.
MINCO는 Trajectory with Minimum Control (논문 ref: Geometrically Constrained Trajectory Optimization for Multicopters)로, 드론의 motion을 polynomical segments로 표현하며, 최소 control을 사용하는 optimal trajectory를 최적화하는 방법론. (나중에 공부!!)

\mathcal{T}_{MINCO} =\{ s(t):[0,T] \to \mathbb{R}^m | c=\mathcal{M}(q,T),q\in \mathbb{R}^{m(M-1)}, T \in \mathbb{R}^M_{>0} \}

$M$ 개의 polynomial trajectory (segments) = $s(t)$
$q=[q_1,...,q_{M-1}]$ : intermediate points
$T=[T_1,...,T_M]$ : 각 polynomial의 time duration
$c$ : trajectory polynomial의 coefficient → $c=\mathcal{M}(q,T)$ 의 함수로 구할 수 있음 → 이렇게 표현하면 전체 trajectory를 intermediate point $q$ 와 time interval $T$ 로 표현할 수 있게 되서 computational efficiency가 향상

** 최적화에서 최적화하는 변수는 $q$ 와 $T$ !!

$i$ 번째 segment trajectory는 그러면 아래와 같이 $2l-1$ 의 degree를 갖는 polynomial

s_i(t)=c_i^T\beta(t), t\in[0,T_i]

여기서 $c_i \in \mathbb{R}^{2l\times m}$ 은 계수 행렬
$\beta(t)=[1,t,...,t^{2l-1}]^T$ 는 natural basis
이러한 trajectory의 생성 과정은 아래의 multi-objective 최적화 문제를 풀어서 진행

min_{q,T}J(c,T)=\rho_sJ_s(c,T)+\sum_*\sum^M_{i=0}\rho_*J^*_i+\sum_+\sum^M_{i=0}\rho_+J^+_j

$J$ 는 각각의 constraint violation을 포함하는 cost function
$\rho$ 는 cost term의 weight
$M$ 은 polynomial pieces의 갯수
$N$ 은 prediction points의 갯수
$J_s$ : smoothness cost로, trajectory로부터 바로 계산되는 값
뒤의 두개 term은 해당 방법론에서 최적화의 inequality constraint $(\mathcal{G}\le0)$ 에 관련되는 term들
$\mathcal{G}>0$ 일 때만 cost가 적용되고 아니면 0
이러한 constraint는 두 가지로 나뉨
- drone 자체로 인한 constraints ( $*$ )
- target과 관련된 constraints ( $+$ )
Drone Induced constraints
- 시간에 따른 적분을 통해 penalty를 계산. $\bar{w}$ 는 사다리꼴 공식으로 적분하기 위한 계수들
- $\kappa$ 는 sampling된 points
- max() 를 보면 $\mathcal{G} >0$ 일 때만 계산된다는 것을 알 수 있음

J_i^*(c_i,T_i)=\frac{T_i}{\kappa_i}\sum^{\kappa_i}_{k=0}\bar{w}_jmax[\mathcal{G}_*(c_i,T_i,\frac{k}{\kappa_i}),0]^3

Target-associated Constraints
- absolute time에서 penalty를 계산

J^+_j(c_i,T_0,...,T_i)=max[\mathcal{G}_+(c_i,t_j),0]^3

$t_j$ 는 $(i+1)$ 번째 polynomial piece에 위치한 $j$ 번째 prediction time $\sum^i_{h=0}T_h\le t_j \le \sum^{i+1}_{h=0}T_h$

해당 연구에서는 robot translation $p(t)=[x(t), y(t),z(t)]^T$ 를 표현하기 위해 $MINCO|_{l=4,m=3}$ trajectory를 활용하였고, drone yaw angle $\psi(t)$ 와 gimbal angle $\phi(t)$ 를 표현하기 위해 $MINCO|_{l=2,m=2}$ 를 활용했다고 한다.
이제 각각의 constraint에는 어떤 것이 있는지 확인해보자.

Dynamic Constraints

Quadrotor의 differential flatness에 의하면 드론의 state와 input은 flat output들에 의해 표현될 수 있기 때문에, vel, acc, att, bodyrate가 직접적으로 trajectory로부터 계산될 수 있다고 한다.

\begin{bmatrix} v \\ a \\ q \\ w \end{bmatrix} = \Psi(x,y,z,\psi)

$\Psi$ 는 differential flatness mapping 함수로, 최적화 시, 이 함수의 역함수로 gradient를 propagate시킬 수 있다.

** Differential flatness

한 시스템에서 어떤 flat output이 있어서, 시스템의 모든 state와 input을 이 flat output들과 이의 미분들의 smooth function으로 표현할 수 있다면 differentially flat하다고 한다.
Quadrotor에서 이러한 flat output은 position (x,y,z)와 yaw와 그 미분들 (vel, acc, jerk, yaw rate), 이를 통해 state 와 input (torque, thrust, …)를 표현할 수 있음
이렇게 하면, 내가 원하는 output을 specify하면 이를 달성하기 위한 control input을 직접적으로 구할 수 있게 된다.
즉, planning이나 optimize 시, 드론의 nonlinear dynamic를 explicit하게 다룰 필요가 없어진다.
또한 optimization을 수행 시, cost function에 대한 state나 input의 gradient를 flat output들로 propagate할 때, flatness mapping 함수의 역함수를 활용할 수 있는것이다.

quarotor와 gimbal rate의 physical constraint는 아래와 같이 쓸 수 있다.

\mathcal{G}_r=||r(t_k)||^2-r^2_{max}, r\in\{v,a,w\}

\mathcal{G}_\phi=||\dot{\phi}(t_K)||^2-\dot{\phi}_{max}^2

Safety Constraints

먼저, trajectory가 collision free해야 하기 때문에, 드론의 position이 frone-end에서 구한 polyhedon안에 위치해야한다.

\mathcal{G}_c=A_f \cdot p(t_k)-b_f

또한, mapping이 되지 않은 영역을 탐색할 때에 mapping을 하기 위해서 드론의 heading이 velocity direction과 align되어야 한다. (특정 threshold보다 차이가 작도록)

\mathcal{G}_\psi = || \psi(t_k)-\psi_v(t_k)||^2-\psi^2_{thr}

\psi_v=atan2(v_y,v_x)

Videography Constraints

위에서 View Region에서 언급했듯이, shooting angle $\Theta$ 와 distance $\mathcal{D}$ 는 view region $\mathcal{V}$ 에 의해 handling. → 그러므로 최적화 중에는 드론의 position이 아래와 같은 polyhedron으로 constrained

\mathcal{G}_{view}=A_v \cdot p(t_j)-b_v

또 다른 videography parameter인 $\{ \mathcal{P}, \dot{\mathcal{P}} \}$ 는 state variables $p,v,q,w,\phi, \dot{\phi}$ 에 의해 결정된다.
Camera frame에서 물체의 위치 $\pi=[\pi_x, \pi_y, \pi_z]^T$ 는 아래와 같이 구해질 수 있다.

\phi=R^c_b(\phi)[R^b_w(q)(\xi-p)-p^b_c)

$R^b_w(q)$ 는 body attitude quaternion $q$ 로부터 구해질 수 있고,
$R^c_b(\phi)$ 는 gimbal rotation $\phi$ 로부터 구해질 수 있다.
$p^b_c$ 는 이미 알고 있는 값 (translation)
Pinhole camera model을 가정하면, (Intrinsic known)

\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} F_x\pi_x/\pi_z + C_x \\ F_y\pi_y/\pi_z + C_y \end{bmatrix}

\begin{bmatrix} \dot{u} \\ \dot{v} \end{bmatrix} = \begin{bmatrix} F_x(\dot{\pi}_x\pi_z - \dot{\pi}_z\pi_x) / \pi_z^2 \\ F_y(\dot{\pi}_y\pi_z - \dot{\pi}_z\pi_y) / \pi_z^2 \end{bmatrix}

위의 식에서 projected velocity $\dot{\pi}$ 를 구하기 위해 $\pi$ 를 미분하면, ( $S$ 는 skew-symmetric matrix)

\dot{\pi}=S(\dot{\phi})^TR^c_b(\phi)[R^b_w(q)(\xi-p)-p^b_c] \\+R^c_b(\phi)[S(w)^TR^b_w(q)(\xi-p)+R^b_w(q)(\dot{\xi}-v)]

이때, pixel value에서 발생하는 너무 큰 cost로 인한 문제를 해결하기 위해 sigmoid 함수를 사용 → 그러면 image position과 image velocity에 대한 cost는 아래와 같이 쓸 수 있음

J^p_j(c_i,T_0,...,T_i)=\sigma(||\begin{bmatrix} u-\mathcal{U}_{img} \\ v-\mathcal{V}_{img} \end{bmatrix} ||)

J^v_j(c_i,T_0,...,T_i)=\sigma(||\begin{bmatrix} \dot{u}-\dot{\mathcal{U}}_{img} \\ \dot{v}-\dot{\mathcal{V}}_{img} \end{bmatrix} ||)

Code study

https://github.com/ZJU-FAST-Lab/Auto-Filmer/tree/main?tab=readme-ov-file

FASTLAB의 연구들 코드 베이스는 거의 다 비슷하다.
보통 크게는 아래와 같은 구조로 이루어져 있다.
- Target motion prediction model : 보통 bbox 기반으로 위치 추정
- mapping : Depth map을 기반으로 gridmap을 생성한다.
- planning : 가장 메인이 되는 파트로, 드론과 타겟의 odometry, 여러 정보 (map 등)를 추합하여 trajectory planning을 수행
- traj_server : planning에서 만들어진 trajectory를 적절한 position cmd로 바꿔준다.
- uav_simulator : so3_quadrotor & so3_controller로 이루어져 있으며, 시뮬레이션 드론을 만들어 쓴다. position cmd를 받고 실제로 움직임을 simulate해서 odom을 보내준다.
- odom_visualization : rviz에 odom 보여주기 위한 파트
다른 부분은 거의 공통적이고, planning이 연구의 메인

Planning_nodelet.cpp

Core code → planning_nodelet.cpp : front-end planning + back-end optimization + mapping + target tracking
Subscribed topics
- odom
- gimbal
- gridmap_inflate
- trigger
- shot
- target
plan_timer_callback() → main trajectory planning function

Shared pointers

planning_nodelet.cpp에 사용되는 여러 모듈들

gridmapPtr_ = std::make_shared<mapping::OccGridMap>();
envPtr_ = std::make_shared<env::Env>(nh, gridmapPtr_);
pathPtr_ = std::make_shared<path::PathSearch>(nh, gridmapPtr_);
visPtr_ = std::make_shared<visualization::Visualization>(nh);
trajOptPtr_ = std::make_shared<traj_opt::TrajOpt>(nh);
prePtr_ = std::make_shared<prediction::Predict>(nh);
shotPtr_ = std::make_shared<shot::ShotGenerator>(nh);

plan_timer_callback() : planning process

planning_nodelet.cpp의 main 함수

subscribed topics 확인
- odom : odom_p, odom_v, odom_q → yaw = atan2(odom_q .y, odom_q .x)
- gimbal : gimbal_states (angle, rate)
- map : gridmapPtr
- target : target_p, target_v
- shot : shot configuration
ReplanState
- planning 상태를 tracking하기 위한 메세지
- 아래의 정보를 담고 있음
  - drone의 current state
  - target의 predicted state
  - gridmap

Shotconfig generation
- predict_n만큼 shotconfig를 생성
```
shotPtr_ -> generate(shotcfg_list, predict_n);
```
- 설정한 transition time동안 n개의 configuration을 생성
- 기존의 config부터 desired config까지 interpolation해서 n-prediction동안 필요한 configuration을 설정
Predict target state
- predict_n 만큼 predict
```
prePtr_->predict(target_p, target_v, target_predcit, target_vels); 
```
: prePtr은 target prediction module
- target의 위치와 속도를 예측
- predict target yaw : target의 예측된 속도를 이용해 target yaw를 계산, 이를 target_headings로 $yaw=atan2(v_y,v_x)$

Kinodynamic A-star

generate_new_traj_success = pathPtr_->findPath(target_predcit, target_headings, shotcfg_list, 
                                                                                    iniState.col(0), iniState.col(1), kAstar_path);

kAstar_path 라는 3d vector에 담김
target의 predicted position, heading 과 shotconfig를 input으로 받고, A-star trajectory를 계산
Astar topic → x,y,z positions

A-star cost

논문 내용과 동일하게 타겟과 드론의 상대적인 벡터를 기반으로 distance, tilt, angle을 계산하여 사용

여기서, angle은 상대적인 위치 벡터를 기반으로 고려하기 때문에 orientation은 아직 영향을 주지 않음

inline double score(const Eigen::Vector3d& p, const Eigen::Vector3d& target, const double& target_yaw, const shot::ShotConfig& shotcfg)
  {
    double d, angle, des_d, des_angle, delta_angle, best_tilt, des_z;
    Eigen::Vector3d dp = p - target;
    // 1. distance
    des_d = shotcfg.distance;
    d = dp.norm();
    // 2. tilt
    best_tilt = atan((shotcfg.image_p(1) - cy_) / fy_);
    des_z = target.z() + shotcfg.distance * sin(best_tilt);
    // if ground limits, then best_z is clearance_d_
    // if(des_z < clearance_d_)
    //     des_z = clearance_d_;

    // des_tilt = asin((des_z - target.z()) / shotcfg.distance);
    // tilt = asin(dp(2) / d);
    // 3. pan
    angle = std::atan2(dp(1), dp(0));
    des_angle = shotcfg.view_angle + target_yaw;
    delta_angle = fabs(des_angle - angle);
    while(delta_angle > 2*M_PI)
        delta_angle -= 2*M_PI;
    delta_angle = std::min(delta_angle , 2*M_PI - delta_angle);
    return lambda_cost * (fabs(d - des_d) + lambda_theta * delta_angle + lambda_z * fabs(p.z() - des_z)); 
  }

View Region Construction
```
generate_new_traj_success = envPtr_->generate_view_regions(target_predcit, target_headings, shotcfg_list, 
                                            kAstar_path, visible_ps, view_polys);
```
- initial path를 기준으로 visible_ps, view_polys 를 생성
- visible_ps를 기반으로 view_polys (ploytope)를 만드는 것
- 여기서도 마찬가지로 target에 대한 visibility를 보장하는 view region에 대해 드론의 position을 constraint하는 부분이기 때문에, orientation은 영향을 주지 않음

replan decision
- 현재까지의 과정에서 replan 여부 결정
  - 드론의 속도와 타겟 속도가 낮을 때
  - visible ps와 현재 드론 위치가 충분히 가까울 때
Corridor Generation
```
envPtr_->pts2path(visible_ps, path);
envPtr_->generateSFC(path, 2.0, hPolys, keyPts);
```
- visible_ps를 기반으로 path를 생성
- 그 path를 기반으로 safe flight corridor (polyhedron) 생성 → hPolys

Trajectory Optimization

generate_new_traj_success = trajOptPtr_->generate_traj(iniState, 
                                                       finState,
                                                       iniAngle,
                                                       target_predcit,
                                                       target_vels,
                                                       view_polys,
                                                       des_pos_image,
                                                       des_vel_image,
                                                       hPolys, traj);
pub_traj(traj, replan_stamp);

initial path를 기반으로 MINCO polynomial trajectory 생성
initState는 [odom_p, vel, acc , jerk] (column vector 4개 → 3x4 mat)
initAngle은 [[now_yaw, 0],[gimbal angle, gimbal rate]] (2x2 mat)
finState는 [path.back(), target_v, 0, 0] (col vec 4개 → 3x4 mat)
des_pos_image & des_vel_image 는 shot config로부터 받아온 값
output : traj → x,y,z,psi,theta,duration 의 sequence

Optimization

trajOptPtr 의 main 함수인 generate_traj 에서 initial trajectory와 input states를 통해 최적화된 경로 계획

bool TrajOpt::generate_traj(const Eigen::MatrixXd& iniState,
                            const Eigen::MatrixXd& finState,
                            const Eigen::MatrixXd& iniAngle,
                            const std::vector<Eigen::Vector3d>& target_predcit,
                            const std::vector<Eigen::Vector3d>& target_vels,
                            const std::vector<Eigen::MatrixXd>& view_polys,
                            const std::vector<Eigen::Vector2d>& des_pos_image,
                            const std::vector<Eigen::Vector2d>& des_vel_image,
                            const std::vector<Eigen::MatrixXd>& hPolys,
                            Trajectory& traj) {
                            
...

setBoundConds(iniState, finState, iniAngle);

...

int opt_ret = optimize();

...

mincoOpt_.setParameters(P, psi_, theta_, T);
mincoOpt_.getTrajectory(traj);

...

setBoundConds 함수 : 최적화시 initial, final boundary condition을 설정
- 먼저 initState와 finState의 velocity, acceleration이 정해진 limit을 넘어가지 않도록
- initial & final yaw 설정 : setAngleInitValue()
  - drone yaw : control point position을 기반으로 $atan2$ 를 활용한 velocity direction으로 interYaw를 계산
  - gimbal yaw : target에 heading을 맞추기 위해 target의 위치와 내 위치의 각도를 atan2로 interTheta 계산
    
    → iniAngle과 finAngle도 똑같이 선언
- mincoOpt_ 에 condition set


void TrajOpt::setBoundConds(const Eigen::MatrixXd& iniState,
                            const Eigen::MatrixXd& finState,
                            const Eigen::MatrixXd& iniAngle) {
  ...
  
  initS.col(1) *= tempNorm > vmax_ ? (vmax_ / tempNorm) : 1.0;
  tempNorm = finalS.col(1).norm();
  finalS.col(1) *= tempNorm > vmax_ ? (vmax_ / tempNorm) : 1.0;
  tempNorm = initS.col(2).norm();
  initS.col(2) *= tempNorm > amax_ ? (amax_ / tempNorm) : 1.0;
  tempNorm = finalS.col(2).norm();
  finalS.col(2) *= tempNorm > amax_ ? (amax_ / tempNorm) : 1.0;

  ...
  
  setAngleInitValue(iniAngle, T, P, finPos, iniAngleAdjust, finAngleAdjust, interAngle);
  
  ...
  
  mincoOpt_.setConditions(initS, finalS, iniAngleAdjust, finAngleAdjust, N_);

  ...
}

Optimize 함수
- optimize 수행
- L-BFGS (limited-memory broyden-fletcher-goldfarb-shanno) solver는 flat array x_를 필요로 함
- t, p, psi, theta는 x_를 각각 특정 slice별로 map시킨 변수들
- 초기값은 t_, p_, psi_, theta_로 넣어줌
- optimize를 마친 후, x_ 값을 t_, p_, psi_, theta_에 넣어줌
- objectiveFunc 함수에 cost, grad 정의
- grad propagate를 통한 최적화 변수 update

int TrajOpt::optimize(const double& delta) {

  ...
  
  Eigen::Map<Eigen::VectorXd> t(x_, dim_t_);
  Eigen::Map<Eigen::VectorXd> p(x_ + dim_t_, dim_p_);
  Eigen::Map<Eigen::VectorXd> psi(x_ + dim_t_ + dim_p_, dim_psi_);
  Eigen::Map<Eigen::VectorXd> theta(x_ + dim_t_ + dim_p_ + dim_psi_, dim_theta_);
  t = t_;
  p = p_;
  psi = psi_;
  theta = theta_;
  
  ...
  
  auto ret = lbfgs::lbfgs_optimize(dim_t_ + dim_p_ + dim_psi_ + dim_theta_ + 1, x_, &minObjective,
                                   &objectiveFunc, nullptr,
                                   &earlyExit, this, &lbfgs_params);
  ...
  
  
  t_ = t;
  p_ = p;
  psi_ = psi;
  theta_ = theta;
  return ret;
}

objectiveFunc
- optimize하기 위한 cost를 계산하기 위한 함수
- cost를 바탕으로 각 variable의 gradient를 계산

static inline double objectiveFunc(void* ptrObj,
                                   const double* x,
                                   double* grad,
                                   const int n) {
  ...

  obj.dbg_msg.cost_smooth = cost;
  obj.mincoOpt_.getEnergy(cost, obj.rhoSmooth_);
  
  ...
  
  // this function add intergral penalty like pos, vel and acc
  obj.addTimeIntPenalty(T, b, b_angle, cost, obj.partialGradByTimes, 
                            obj.partialGradByCoeffs, obj.partialGradByCoeffsAngle, obj.flatmap_);
  
  obj.addTimeCost(T, b, b_angle, cost, obj.partialGradByTimes, obj.partialGradByCoeffs, 
                            obj.partialGradByCoeffsAngle, obj.flatmap_);

  obj.mincoOpt_.propogateGrad(obj.partialGradByCoeffs, obj.partialGradByCoeffsAngle, obj.partialGradByTimes, 
                                        obj.gradByPoints, obj.gradByAngles, obj.gradByTimes);

  ...
}

addTimeIntPenalty : 논문에서 time integral penalty에 해당
- corridor cost (cost_corridor) : drone이 polyhedron안에 위치하도록 (related : clearance_d)
- velocity, acceleration, angular rate (cost_v, cost_a, cost_omg) : limit 값을 지키도록 (related : vmax, amax, ratemax)
- safety (cost_mapping) : 드론의 yaw와 heading이 같은 방향을 가르키도록 (related : rhoMapping)
addTimeCost : 논문에서 absolute time penalty에 해당
- view region cost (cost_view) : view region안으로 들어오도록 (related : rhoViewPos
- actor safety (cost_actor_safe) : drone이 target와 일정 수준의 거리를 유지 하도록 (related : rhoNoKilling)
- visiblity (cost_visibility) : image plane 내에서 보이는 타겟이 원하는 위치와 속도를 가지도록 (related : rhoVisibilityPos, rhoVisibilityVel)

Discussion

shot parameter를 만족하도록 경로를 최적화하는 연구.
ZJU FASTLAB의 다양한 uav tracker (Elastic Tracker, Fast Tracker 등) 여러 연구와 framework가 비슷해서 한번 코드 structure를 알아두면 재 사용하기가 편하다.
그리고 해당 연구들은 trajectory를 표현하고 최적화하는데 있어서 MINCO trajectory class (Geometrically Constrained Trajectory Optimization for Multicopters) 를 사용하는데, 나중에 각잡고 공부해보는 것도 좋을 것 같다. (너무 어려워서…)
https://github.com/ZJU-FAST-Lab/GCOPTER
https://arxiv.org/pdf/2103.00190

전반적으로 intuitive하고 ros로 실제 적용해보기 어렵지 않기 때문에 좋은 연구라고 생각한다.
또한 cost function을 잘 설계해서 내가 원하는 constraint을 잘 부여해보는 것도 재미있을 것 같다.

신희준

공부하고 싶은 사람

이전 포스트