PAMPC: Perception-Aware Model Predictive Control for Quadrotors 리뷰

신희준·2024년 11월 27일
ControlUAV

Paper Review

목록 보기
29/30

Paper : [PAMPC: Perception-Aware Model Predictive Control for Quadrotors] (https://arxiv.org/abs/1804.04811 (Davide Falanga, Philipp Foehn, Peng Lu, Davide Scaramuzza / IEEE IROS 2018)

code: https://github.com/uzh-rpg/rpg_mpc

video : https://www.youtube.com/watch?v=9vaj829vE18

Highlights

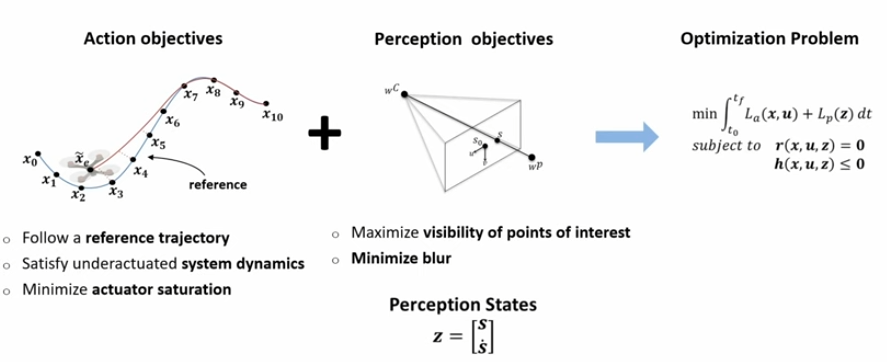
  • Perception-Aware Model Predictive Controller를 제안
  • Action과 Perception objectives를 하나의 MPC optimization problem으로 unify
    → 즉, MPC에 camera sensing에 관련된 objective를 추가했다고 볼 수 있겠음
    → 여기서 objectives라 함은
    • Quadrotor system dynamics and input limits를 고려
    • Image plane에서 point of interest의 visibility를 향상
    • Point of interest의 projected velocity를 감소 (이미지 상에서 POI의 속도를 최소화)

→ 이를 통해 생성된 trajectory는 POI를 image centre에 잘 유지할 수 있음

  • Onboard low-power ARM computer에서 real-time으로 잘 작동

Introduction

  • Perception algorithm의 발전으로, 카메라를 활용한 vision-based 조종이 빠르게 발전

  • 하지만 vision-based perception은 몇 가지 한계가 있음

    • texture distribution이나 light condition과 같은 환경에 크게 영향을 받음

    • robot motion에도 영향을 많이 받음 (motion blur, camera pointing direction, 등)

      → perception과 action이 항상 함께 고려되어야만 함

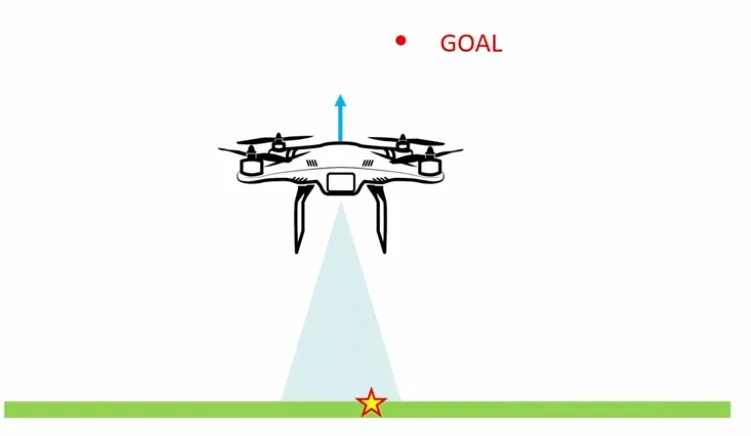
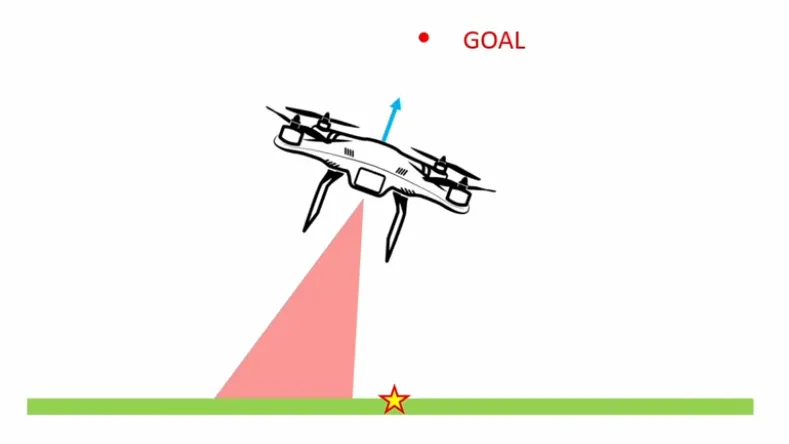
  • 예를 들어, 어떤 좁은 통로를 지나기 위해 camera sensor로 localization하기 위해서는 이 통로가 계속해서 보일 수 있도록 action을 취해줘야 함.

MPC 간단 정리

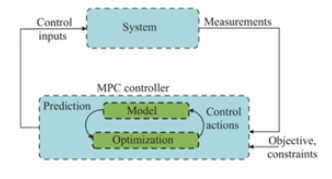
  • MPC (Model Predictive Control)는 Optimization-based feedback controller.

    → Dynamics 모델을 이용해 short time horizon에 대한 미래 state를 예측

    → reference trajectory 또는 desired pose에 대한 cost를 최소화하도록 control을 반복적으로 갱신

    ✅ 위 그림에 비교하여 설명

    • measurement는 현재 state
    • system dynamics model을 활용하여 미래 state를 예측
      xk+1=f(xk,uk)x_{k+1}=f(x_k,u_k)
    • Objective + constraints를 만족하는 control sequence 계산 → optimization
    • Control sequence 중 가장 첫번째 control을 system에 입력

  • 이를 위해 MPC는 quadrotor의 dynamic model과 optimization process를 필요로 함

  • 일반적인 MPC는 다음과 같은 process를 진행

    1. 현재 state를 입력으로 받음

    2. 정해진 timestep horizon의 최적화 문제를 solve

      → 이때 dynamics + cost + constraints 고려

    3. 최적의 control sequence 계산

    4. 첫 control만 적용하고 다시 반복

  • 특히 PAMPC에서 활용한 Nonlinear RTI-SQP문제의 경우 내부적으로는

    1. 현재 state를 초기 조건으로 두고 최적화 과정에서 future trajectory 계산
    2. 비선형 dynamics와 cost를 현재 trajectory 주변에서 선형화/이차 근사하여 Quadratic Programming을 구성
    3. 이전 iteration의 solution을 초기값으로 사용하여 reference, cost, constraints를 포함한 QP를 solve
    4. 계산된 solution은 현재 linearization 기준에서 근사해이며, 이를 매 timestep 반복하여 실제 optimum 추종 (시간이 흘러가면서 점차 최적화)
    5. 위 과정 반복

  • optimization이 constraints들을 다룰 수 있기 때문에, actuator limitation과 같은 외부 요인들을 다룰 수 있게 됌 → classical controller에 비해서 갖는 장점

  • 미래 horizon 전체에 대해 cost를 평가할 수 있기 떄문에 여러 목적을 하나의 cost function으로 통합하기에 용이

Contributions

  • Action과 Perception objective를 동시에 최적화하는 MPC 알고리즘 제안 → 이를 통해 생성된 trajectory는 robot dynamic을 만족시키면서 POI의 visibility를 보장

  • Action objective와 Perception objective의 potential conflict를 numerical optimization으로 해결

    • perception objective를 constraint가 아닌 optimization component로 여김
    • perception을 cost function으로 합치는 것이 computational complexity를 줄여줌

  • 또한, 이러한 방법을 통해 vision-based localization, target tracking 등의 성능을 높일 수 있다.

    • land mark visibility가 높아지고, image plane velocity가 낮아지기 때문

Problem Formulation

  • 자율로봇항법을 위해서는 두 가지 요소가 필수적

    • Perception : ego-motion과 surrounding environment
    • Action : combination of motion planning and control algorithm

  • 이때 perception과 action의 coupling은 상당히 중요함

    • 안전한 비행을 위해서 정확하고 robust한 perception이 필수적인데, vision-based perception의 quality는 camera motion에 많이 영향을 받음
    • 또한 image로부터 충분한 정보를 추출할 수 있도록 해줘야 적절한 action을 취할 수 있음

  • 시스템은 아래와 같이 정의할 수 있음

    • xx와 uu는 robot의 state와 input vector라고 하자.
    • 로봇의 dynamic은 미분방정식으로 표현 x˙=f(x,u)\dot{x}=f(x,u)
    • zz는 perception system의 state vector (e.g., image plane으로의 3D point projection)
    • σ\sigma는 perception 특성 parameter의 vector (e.g., camera의 focal length나 FOV)

  • perception state와 robot state는 robot dynamic를 통해 coupled

z=fp(x,u,σ)z=f_p(x,u,\sigma)
  • 특정 action objective가 주어진 상황에서 action cost La(x,u)\mathcal{L}_a(x,u)와 perception cost Lp(z)\mathcal{L}_p(z)를 정의할 수 있고, 이를 통해 최적화 문제로 이 coupling을 공식화할 수 있음
minu∫t0tfLa(x,u)+Lp(z)dtsubjected to   r(x,u,z)=0,  h(x,u,z)≤0min_u \int^{t_f}_{t_0} \mathcal{L}_a(x,u)+\mathcal{L}_p(z)dt \\ \text{subjected to } \; r(x,u,z)=0, \; h(x,u,z) \leq 0
  • rr과 hh는 perception, action이 동시에 만족해야하는 제약 조건을 의미
    • 보통 equality constraints는 system dynamics를 의미. 여기서는 perception 추가되었을 것
    • 보통 inequality constraints는 입력 제한이나 상태 제한 등.

Methodology

  • robot의 navigation을 위한 computer vision 알고리즘은 두 가지 기본적인 requirements가 존재

    • 알고리즘에 사용될 Point of interest가 이미지에 항상 보여야한다. 예를 들어 visual odometry알고리즘의 pose estimation을 위해서 landmark와 같은 point들이 필요

    • 그런 point of interest들이 image에서 명확하게 recognizable해야함. camera의 motion이나 scene까지의 거리로 인해 motion blur 등이 생길 수 있음

      → 그러므로 camera의 motion은 robust한 visual perception을 보장할 수 있도록 계획되어야 함

  • 이러한 고려를 바탕으로 이 연구에서는 perception object로써 다음의 두 가지를 고려

    • visibility of point of interest
    • minimization of the velocity of their projection onto the image plane

  • 이를 위해 quadrotor에 장착된 카메라의 motion과 3d 공간의 point의 image plane으로 projection 사이의 관계를 파악해야함

    → quadrotor의 state와 input vector의 함수를 통해 image plane으로의 projection dynamic을 표현하여, perception과 action을 하나의 optimization으로 couple

Nomenclature

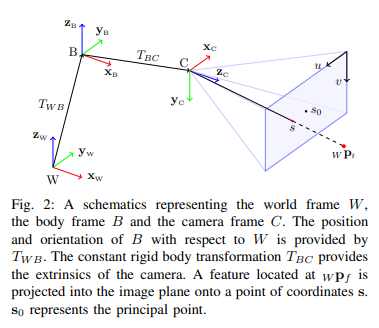
  • 먼저, world frame WW, quadrotor frame BB, camera frame CC를 정의

  • 벡터의 표현의 경우, WPWB_WP_{WB}는 body frame BB를 world frame에 대한 position을 world frame에서 표현한 것

  • 강체의 orientation을 표현하기 위해서는 quaternion 사용

  • 쿼터니언 q=(qw,qx,qy,qz)Tq=(q_w,q_x,q_y,q_z)^T의 시간 미분은 아래와 같이 정의

q˙=12Λ(w)⋅q\dot{q}=\frac{1}{2}\Lambda(w) \cdot q
  • 벡터 w=(wx,wy,wz)Tw=(w_x,w_y,w_z)^T의 skew-symmetric matrix Λ(w)\Lambda(w)는 아래와 같이 표현
Λ(ω)=[0−ωx−ωy−ωzωx0ωz−ωyωy−ωz0ωxωzωy−ωx0]\Lambda(\omega) = \begin{bmatrix} 0 & -\omega_x & -\omega_y & -\omega_z \\ \omega_x & 0 & \omega_z & -\omega_y \\ \omega_y & -\omega_z & 0 & \omega_x \\ \omega_z & \omega_y & -\omega_x & 0 \end{bmatrix}
  • operator ⊙\odot은 quaternion과 vector의 곱으로 사용. → 이는 벡터 vv를 quaternion qq만큼 회전시키는 것을 의미 즉, 회전한 새 벡터 v′v'는 아래와 같이 구할 수 있음
v′=v⊙q=Qvv'=v \odot q=Qv
Q=[1−2qy2−2qz22(qxqy+qwqz)2(qxqz−qwqy)2(qxqy−qwqz)1−2qx2−2qz22(qyqz+qwqx)2(qxqz+qwqy)2(qyqz−qwqx)1−2qx2−2qy2]Q = \begin{bmatrix} 1 - 2q_y^2 - 2q_z^2 & 2(q_xq_y + q_wq_z) & 2(q_xq_z - q_wq_y) \\ 2(q_xq_y - q_wq_z) & 1 - 2q_x^2 - 2q_z^2 & 2(q_yq_z + q_wq_x) \\ 2(q_xq_z + q_wq_y) & 2(q_yq_z - q_wq_x) & 1 - 2q_x^2 - 2q_y^2 \end{bmatrix}

Quadrotor Dynamics

  • world frame에서 표현된 body의 position과 orientation
pWB=(px,py,pz),  qWB=(qw,qx,qy,qz)Tp_{WB} = (p_x,p_y,p_z), \; q_{WB}=(q_w,q_x,q_y,q_z)^T
  • world frame에서 표현된 body의 linear velocity
vWB=(vx,vy,vz)Tv_{WB}=(v_x,v_y,v_z)^T
  • body frame에서 표현된 angular velocity
ΩB=(wx,wy,wz)T\Omega_B=(w_x,w_y,w_z)^T
  • mass-normalized thrust vector (fif_i는 i번째 모터의 출력)
c=(0,0,c)Tc=(f1+f2+f3+f4)/mc=(0,0,c)^T \\ c= (f_1+f_2+f_3+f_4)/m
  • 그러면 아래와 같이 quadrotor의 dynamic model을 정의할 수 있음
p˙WB=vWBv˙WB=wg+qWB⊙cq˙WB=12Λ(ΩB)⋅qWB\dot{p}_{WB}=v_{WB} \\ \dot{v}_{WB}=wg+q_{WB} \odot c \\ \dot{q}_{WB} = \frac{1}{2} \Lambda(\Omega_B) \cdot q_{WB}
  • state vector와 input vector는 다음과 같음
x=[pWB,vWB,qWB]T,  u=[c,ΩBT]Tx=[p_{WB},v_{WB}, q_{WB}]^T ,\; u=[c, \Omega^T_B]^T

Perception Objectives

  • Point of interest (landmark)의 3D 위치를 world frame에서 표현한 점
Wpf=(Wpfx,Wpfy,Wpfz)_Wp_f=(_Wp_{fx}, _Wp_{fy}, _Wp_{fz})
  • constant rigid body transformation (camera의 extrinsic parameter)
TBC=[pBC,qBC]T_{BC}=[p_{BC},q_{BC}]
  • Wpf_Wp_f는 camera frame에서 표현할 수 있다.
Cpf=(qWBqBC)−1⊙(Wpf−(qWB⊙pBC+pWB))_Cp_f=(q_{WB}q_{BC})^{-1}\odot (_Wp_f-(q_{WB}\odot p_{BC}+p_{WB}))
  • camera frame에서의 점 Cpf_Cp_f은 pinhole camera model에 의해 image coordinate s=(u,v)Ts=(u,v)^T로 projection 가능
u=fxCpfxCpfz,  v=fyCpfyCpfxu=f_x\frac{_Cp_{fx}}{_Cp_{fz}}, \; v=f_y\frac{_Cp_{fy}}{_Cp_{fx}}

  • Robust한 vision-based perception을 위해서는 POI wpf_wp_f의 projection ss가 최대한 이미지의 center에 위치해야한다.

    • 외란에 대해 높은 safety margin을 가질 수 있기 때문
    • 이미지의 외각에서 보통 많은 왜곡이 발생

  • POI가 이미지에서 계속 보이게 하기 위해서, 이들의 image plane으로의 projection들의 velocity가 줄어야 한다.

  • POI가 정적이라고 가정했을 때, projection들의 속도를 quadrotor의 state와 input vector로 표현할 수 있다. 이를 위해서 ss를 시간에 대해 미분한다.

u˙=fxCp˙fxCpfz−CpfxCp˙fzCpfz2\dot{u}=f_x\frac{_C\dot{p}_{fx} {_C}p_{fz}-_Cp_{fx} {_C}\dot{p}_{fz}}{_Cp^2_{fz}}
v˙=fyCp˙fyCpfz−CpfyCp˙fzCpfz2\dot{v}=f_y\frac{_C\dot{p}_{fy} {_C}p_{fz}-_Cp_{fy} {_C}\dot{p}_{fz}}{_Cp^2_{fz}}
  • 정리하면
s˙=[u˙v˙0]=[0−fxCpfz20fyCpfz200000](Cpf×Cp˙f)\dot{s} = \begin{bmatrix} \dot{u} \\ \dot{v} \\ 0 \end{bmatrix} = \begin{bmatrix} 0 & -\frac{f_x}{_Cp^2_{fz}} & 0 \\ \frac{f_y}{_Cp^2_{fz}} & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} (_Cp_f \times _C\dot{p}_f)
  • Cp˙f_C\dot{p}_f를 계산하기 위해서는 Cpf_Cp_f를 시간에 대해 미분
Cp˙f=−12Λ(ΩC)Cpf−CvWC_C\dot{p}_f = -\frac{1}{2} \Lambda(\Omega_C) _Cp_f - _Cv_{WC}
CvWC=(qWBqBC)−1⊙[12Λ(ΩB)qWB⊙pBC+vWB],ΩC=qBC−1⊙ΩB._Cv_{WC} = (q_{WB} q_{BC})^{-1} \odot \left[ \frac{1}{2} \Lambda(\Omega_B) q_{W B} \odot p_{B C} + v_{W B} \right], \\ \Omega_C = q_{B C}^{-1} \odot \Omega_B.

Action Objectives

  • Quadrotor가 3d space에서 원하는 위치에 도달하게 하기 위해서는 적절한 trajectory 계획이 필요한데, 이를 위해서 두 가지의 objective가 고려되어야 함
    • System의 available bounded inputs : motor의 thrust가 upper & lower bound를 지켜야 한다. → limited input vector uu
    • Underactuated nature of a quadrotor : control inputs (thrust, roll, pitch, yaw)가 독립적으로 모든 degree of freedom을 가지고 control할 수 없다는 system dynamics를 고려해야 한다.

Challenges

  • Perception과 Action을 동시에 고려하는 것은 conflict가 발생할 수 있기 때문에 challenging.

  • 예를 들어, quadrotor가 reference trajectory를 track하기 위해서는 원하는 acceleration의 방향으로의 추력을 주기 위해 rotate해야하지만, perception objective가 POI의 visibility를 최대화하기 위해 그러한 rotation을 minimize해야할 수도 있다.

  • 그러므로 system dynamics를 통해 이 둘을 coupling시켜 둘 다 고려할 수 있는 model-based optimization framework가 필요하다.

Model Predictive Control

  • Perception과 action의 coupled된 문제를 optimization 문제로 푸는 것은 기존의 classical control (PID)에 비해서 몇 가지 장점을 가진다.

    1. System dynamics를 고려할 수 있다. (underactuated dynamics)
    2. Input constraint를 고려할 수 있다. (Input bound)
    3. Dynamic한 trajectory를 생성할 수 있다.
    4. Future cost prediction을 고려하여 최소화할 수 있다.

  • 이러한 optimization의 기본적인 공식은 위에서 언급했듯이 아래와 같으며,

minu∫t0tfLa(x,u)+Lp(z)dtsubjected  to  r(x,u,z)=0,  h(x,u,z)≤0min_u \int^{t_f}_{t_0} \mathcal{L}_a(x,u)+\mathcal{L}_p(z)dt \\ subjected \; to \; r(x,u,z)=0, \; h(x,u,z) \leq 0

  • 이러한 quadratic cost를 가지는 non-linear program은 sequential quadratic program (SQP)에 의해 근사될 수 있다. (iterative approximation)

  • 이를 위해서 system dynamics를 time horizon tht_h안에서 time step dtdt로 discretize

xi  ∀i∈[1,N],  ui  ∀i∈[1,N−1]x_i \; \forall i \in [1,N], \; u_i \; \forall i \in [1,N-1]

  • time-varying state cost matrix Qx,i  ∀i∈[1,N]Q_{x,i} \; \forall i \in [1,N] 과 time-varying perception, input cost matrixs를 정의 Qp,i,Ri    ∀i∈[1,N−1]Q_{p,i}, R_i \; \; \forall i \in [1,N-1]. 최종적으로 perception function z=[s,s˙]z=[s,\dot{s}]를 정의

    • 여기서 zz는 quadrotor의 state와 input variable의 함수

  • 그러면 cost function은 아래와 같이 쓸 수 있다.

L=xˉN⊤Qx,NxˉN+∑i=1N−1(xˉi⊤Qx,ixˉi+zˉi⊤Qp,izˉi+uˉi⊤Riuˉi),L = \bar{x}_N^\top Q_{x,N} \bar{x}_N + \sum_{i=1}^{N-1} \left( \bar{x}_i^\top Q_{x,i} \bar{x}_i + \bar{z}_i^\top Q_{p,i} \bar{z}_i + \bar{u}_i^\top R_i \bar{u}_i \right),

  • 여기서 xˉ,zˉ,uˉ\bar{x}, \bar{z}, \bar{u}는 reference와의 차이를 의미.

    • 우리의 경우에는 zz의 reference는 null vector (keep POI center of image와 zero velocity)
    • xx와 uu의 경우에는 precomputed trajectory나 target pose로부터 정해지는 값 (이것이 꼭 필요한 것 같지는 않다.)

  • input uu와 velocty vWBv_{WB}는 아래와 같은 제약조건을 만족해야함

cmin≤c≤cmaxΩmin≤ΩB≤Ωmaxvmin≤vWB≤vmaxc_{min} \le c \le c_{max} \\ \Omega_{min} \le \Omega_B \le \Omega_{max} \\ v_{min} \le v_{WB} \le v_{max}
  • 최적화 문제를 풀 때에는 매 control loop마다 하나의 SQP iteration을 수행하여 최적화 문제의 solution을 approximate하는 식이며, 초기 state로는 onboard에서 따로 돌아가는 Visual-Inertial Odometry pipeline에서 제공되는 가장 최근의 estimate xestx_{est}를 활용한다.
  • 즉, SQP가 full optimization을 수행하지 않고, 적절한 예상치 (외부 알고리즘으로 부터 구한 real state)로부터 최적화를 수행하기 때문에, 훨씬 더 빠르고 정확한 최적화를 수행

Experiments

  • 소형 quadrotart를 통해 실험 진행

  • Qualcomm mvSDK로 VIO 수행

  • ACADO (nonlinear optimization setup framework)와 qpOASES (Quadratic programming solver)를 통해 optimization 수행

  • 예시 실험1. circular flight : 하나의 POI를 정해서 이를 따라 원형 경로를 움직이도록

    • circular reference trajectory를 로봇에게 미리 제공

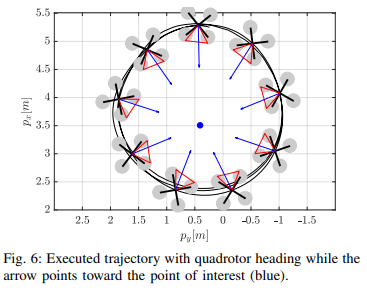
Code 구현

https://github.com/uzh-rpg/rpg_quadrotor_control

https://github.com/uzh-rpg/rpg_mpc

  • controller의 run()함수를 통해 command input을 얻어낸다.
    → MPC가 control loop에서 최적화 한번 돌리고 첫 입력 뽑아 쓰는 것
const quadrotor_common::ControlCommand command = base_controller_.run(
      state_estimate, reference_trajectory_, base_controller_params_);

Control에 필요한 variables

  • State (kStateSize = 10):
    • Position: x,y,z
    • Orientation: Quaternion components (w,x,y,z)
    • Velocity: vx,vy,vz
  • Input (kInputSize = 4):
    • Thrust: T
    • Body rates: p,q,r (angular velocities around the axes)
  • Online data
    • Point of Interest position: (px,py,pz)(p_x, p_y,p_z)
    • Camera-Body translation: (tx,ty,tz)(t_x,t_y,t_z)
    • Camera-Body rotation : (qw,qx,qy,qz)(q_{w},q_x,q_y,q_z)

Quadrotor dynamics

  • 페이퍼에 정의
    p˙WB=vWBv˙WB=wg+qWB⊙cq˙WB=12Λ(ΩB)⋅qWB\dot{p}_{WB}=v_{WB} \\ \dot{v}_{WB}=wg+q_{WB} \odot c \\ \dot{q}_{WB} = \frac{1}{2} \Lambda(\Omega_B) \cdot q_{WB}
  • 코드 구현
    • ⊙\odot 공식에 따라 thrust vector cc를 qWBq_{WB}만큼 회전 시키는 것 확인
    • Λ\Lambda 식도 공식대로
    • << : system에 미분방정식 추가
// Position derivatives
f << dot(p_x) ==  v_x;
f << dot(p_y) ==  v_y;
f << dot(p_z) ==  v_z;

// Quaternion derivatives
f << dot(q_w) ==  0.5 * ( - w_x * q_x - w_y * q_y - w_z * q_z);
f << dot(q_x) ==  0.5 * ( w_x * q_w + w_z * q_y - w_y * q_z);
f << dot(q_y) ==  0.5 * ( w_y * q_w - w_z * q_x + w_x * q_z);
f << dot(q_z) ==  0.5 * ( w_z * q_w + w_y * q_x - w_x * q_y);

// Velocity derivatives (Acceleration)
f << dot(v_x) ==  2 * ( q_w * q_y + q_x * q_z ) * T;
f << dot(v_y) ==  2 * ( q_y * q_z - q_w * q_x ) * T;
f << dot(v_z) ==  ( 1 - 2 * q_x * q_x - 2 * q_y * q_y ) * T - g_z;

Perception Objectives

  • 페이퍼에 따르면 perception objectives에서는 POI의 image로의 projection이 center에 위치해야함

  • 하지만 POI는 world frame에서 정의된 3D 좌표이므로, 아래의 과정이 필요

    • Camera frame에서의 POI 좌표를 계산
    • POI를 image plane으로 projection → 이 projection을 cost function으로 사용해야 함

  • 코드 구현 : 엄청 복잡한 식으로 intermediate state를 정의

// Intermediate states to calculate point of interest projection!
IntermediateState intSx = ((((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*(-(-q_x)*q_B_C_z-q_B_C_w*q_y-q_B_C_x*q_z-q_B_C_y*q_w)+((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)*(-(-q_y)*q_B_C_x-q_B_C_w*q_z-q_B_C_y*q_x-q_B_C_z*q_w)+((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y))*(p_F_x-p_x)+(((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)+((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)+(-(-q_x)*q_B_C_z-q_B_C_w*q_y-q_B_C_x*q_z-q_B_C_y*q_w)*(-(-q_z)*q_B_C_y-q_B_C_w*q_x-q_B_C_x*q_w-q_B_C_z*q_y))*(p_F_y-p_y)+(((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*(-(-q_x)*q_B_C_z-q_B_C_w*q_y-q_B_C_x*q_z-q_B_C_y*q_w)+((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*(-(-q_x)*q_B_C_z-q_B_C_w*q_y-q_B_C_x*q_z-q_B_C_y*q_w)+((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)+((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y))*(p_F_z-p_z));
IntermediateState intSy = ((((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)+((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)*(-(-q_y)*q_B_C_x-q_B_C_w*q_z-q_B_C_y*q_x-q_B_C_z*q_w)+((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)*(-(-q_z)*q_B_C_y-q_B_C_w*q_x-q_B_C_x*q_w-q_B_C_z*q_y))*(p_F_y-p_y)+(((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)+((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)+(-(-q_x)*q_B_C_z-q_B_C_w*q_y-q_B_C_x*q_z-q_B_C_y*q_w)*(-(-q_y)*q_B_C_x-q_B_C_w*q_z-q_B_C_y*q_x-q_B_C_z*q_w))*(p_F_z-p_z)+(((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*(-(-q_y)*q_B_C_x-q_B_C_w*q_z-q_B_C_y*q_x-q_B_C_z*q_w)+((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*(-(-q_y)*q_B_C_x-q_B_C_w*q_z-q_B_C_y*q_x-q_B_C_z*q_w)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y))*(p_F_x-p_x));
IntermediateState intSz = ((((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*(-(-q_x)*q_B_C_z-q_B_C_w*q_y-q_B_C_x*q_z-q_B_C_y*q_w)+((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)*((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)+((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)*(-(-q_z)*q_B_C_y-q_B_C_w*q_x-q_B_C_x*q_w-q_B_C_z*q_y))*(p_F_z-p_z)+(((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)+((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)+((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)*((-q_z)*q_B_C_y+q_B_C_w*q_x+q_B_C_x*q_w+q_B_C_z*q_y)+(-(-q_y)*q_B_C_x-q_B_C_w*q_z-q_B_C_y*q_x-q_B_C_z*q_w)*(-(-q_z)*q_B_C_y-q_B_C_w*q_x-q_B_C_x*q_w-q_B_C_z*q_y))*(p_F_x-p_x)+(((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*(-(-q_z)*q_B_C_y-q_B_C_w*q_x-q_B_C_x*q_w-q_B_C_z*q_y)+((-q_x)*q_B_C_x+(-q_y)*q_B_C_y+(-q_z)*q_B_C_z+q_B_C_w*q_w)*(-(-q_z)*q_B_C_y-q_B_C_w*q_x-q_B_C_x*q_w-q_B_C_z*q_y)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w)+((-q_x)*q_B_C_z+q_B_C_w*q_y+q_B_C_x*q_z+q_B_C_y*q_w)*((-q_y)*q_B_C_x+q_B_C_w*q_z+q_B_C_y*q_x+q_B_C_z*q_w))*(p_F_y-p_y));
  • 실제로는 아래의 내용을 길게 늘어쓴 것

    • World → Camera frame rotation을 계산 : (qWBqBC)−1(q_{WB}q_{BC})^{-1}

    • World → Camera frame translation을 계산 : qWB⊙pBC+pWBq_{WB}\odot p_{BC}+p_{WB}

    • Camera frame에서의 POI

      Cpf=(qWBqBC)−1⊙(Wpf−(qWB⊙pBC+pWB))_Cp_f=(q_{WB}q_{BC})^{-1}\odot (_Wp_f-(q_{WB}\odot p_{BC}+p_{WB}))

→ 즉, intermediate state는 POI의 camera frame 좌표

  • 다음 image plane으로 projection (normalized image plane)
u=fxCpfxCpfz,  v=fyCpfyCpfxu=f_x\frac{_Cp_{fx}}{_Cp_{fz}}, \; v=f_y\frac{_Cp_{fy}}{_Cp_{fx}}
  • 코드
u = intSx / (intSz + epsilon);
v = intSy / (intSz + epsilon);

Cost function and weights

  • Column cost vector hh에 여러 variable 삽입
h << p_x << p_y << p_z
    << q_w << q_x << q_y << q_z
    << v_x << v_y << v_z
    << intSx/(intSz + epsilon) << intSy/(intSz + epsilon) 
    << T << w_x << w_y << w_z;

→ 이 h 값은 timestep마다 계산되는 값이고, 아래는 실제로 상태 x와 control 입력 u에 의해 이렇게 계산된다 라는 것을 선언하는 과정.

→ 그러니까 실제로는 다음과 같은 과정

  1. solver가 최적화 변수 후보 x,ux, u를 하나 선택
  2. 해당 x,ux, u를 h(x,u)h(x,u)에 대입
  3. cost vector hh를 계산
  4. cost ((h−r)TQ(h−r)(h-r)^TQ(h-r) 계산
  • 마지막 cost vector에는 control input은 없음 (time horizon 이후 control 정의 x)
hN << p_x << p_y << p_z
    << q_w << q_x << q_y << q_z
    << v_x << v_y << v_z
    << intSx/(intSz + epsilon) << intSy/(intSz + epsilon);
  • 각 cost element의 weight도 정의
  DMatrix Q(h.getDim(), h.getDim());
  Q.setIdentity();
  Q(0,0) = 100;   // x
  Q(1,1) = 100;   // y
  Q(2,2) = 100;   // z
  Q(3,3) = 100;   // qw
  Q(4,4) = 100;   // qx
  Q(5,5) = 100;   // qy
  Q(6,6) = 100;   // qz
  Q(7,7) = 10;   // vx
  Q(8,8) = 10;   // vy
  Q(9,9) = 10;   // vz
  Q(10,10) = 0;  // Cost on perception
  Q(11,11) = 0;  // Cost on perception
  Q(12,12) = 1;   // T
  Q(13,13) = 1;   // wx
  Q(14,14) = 1;   // wy
  Q(15,15) = 1;   // wz
  • reference 정의
// Set a reference for the analysis (if CODE_GEN is false).
// Reference is at x = 2.0m in hover (qw = 1).
DVector r(h.getDim());    // Running cost reference
r.setZero();
r(0) = 2.0;
r(3) = 1.0;
r(10) = g_z;

DVector rN(hN.getDim());   // End cost reference
rN.setZero();
rN(0) = r(0);
rN(3) = r(3);
  • Cost function 정의 → Least Squared method 사용 : cost vector와 reference vector 사이 차이를 최소화할 수 있도록 cost function을 정의 ✅ reference는 기본적으로 h와 같은 차원을 가지지만 실제로는 내가 원하는 reference에만 값을 넣어주고 나머지는 Q를 활용해 무시
Cost=∑k=0N−1(hk−rk)TQ(hk−rk)+(hN−rN)TQN(hN−rN)Cost=\sum^{N-1}_{k=0}(h_k-r_k)^TQ(h_k-r_k)+(h_N-r_N)^TQ_N(h_N-r_N)
  • 페이퍼에서 cost function 정의 → xˉ,zˉ,uˉ\bar{x}, \bar{z}, \bar{u} 는 reference와의 차이를 의미하므로, 위와 같은 식이고, 단지 cost vector component를 나눠서 써놓은 것
L=xˉN⊤Qx,NxˉN+∑i=1N−1(xˉi⊤Qx,ixˉi+zˉi⊤Qp,izˉi+uˉi⊤Riuˉi),L = \bar{x}_N^\top Q_{x,N} \bar{x}_N + \sum_{i=1}^{N-1} \left( \bar{x}_i^\top Q_{x,i} \bar{x}_i + \bar{z}_i^\top Q_{p,i} \bar{z}_i + \bar{u}_i^\top R_i \bar{u}_i \right),
  • 코드 구현
ocp.minimizeLSQ( Q, h, r );
ocp.minimizeLSQEndTerm( QN, hN, rN );

Discussion

  • UAV control을 위해 PID를 사용하다가 더 많은 constraint를 다루고 싶어서 MPC를 공부
  • MPC 구현을 위해 코드가 함께 있는 study를 알게 되어 리뷰
profile
신희준
공부하고 싶은 사람
이전 포스트

Simple online and realtime tracking with a deep association metric 리뷰

다음 포스트

Auto Filmer: Autonomous Aerial Videography Under Human Interaction 논문 리뷰

0개의 댓글