스택

스택(Stack)

데이터를 임시 저장할 때 사용하는 선형 자료 구조

데이터의 입력과 출력 순서는 후입선출(LIFO, Last In First Out)

즉, 마지막에 넣은 데이터가 가장 먼저 나온다.

---

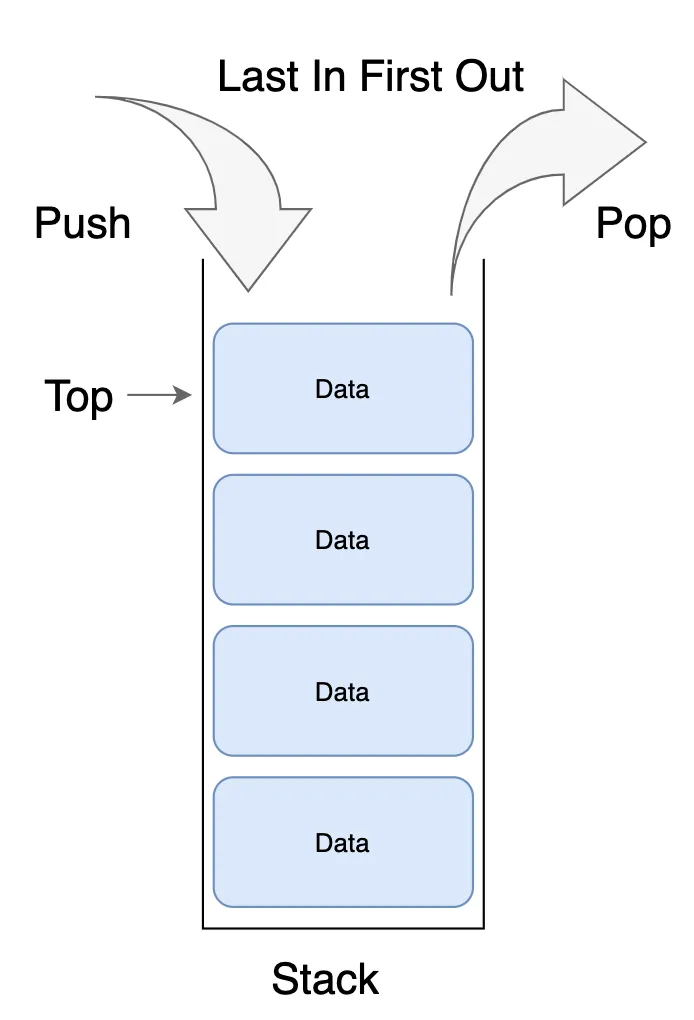
1. 스택의 주요 기능

연산	설명
push()	데이터를 스택의 맨 위(Top)에 추가
pop()	스택의 맨 위(Top) 데이터를 제거하고 반환
top() 또는 peek()	스택의 맨 위(Top) 데이터를 제거하지 않고 반환
clear()	스택의 모든 데이터를 제거
find(value)	특정 값이 스택에 존재하는지 확인
count(value)	특정 값의 개수를 반환
__contains__(value)	in 연산자로 특정 값이 존재하는지 확인
dump()	스택에 있는 모든 데이터를 출력 (디버깅용)

---

2. 스택 포인터(Stack Pointer)

스택에 쌓여있는 데이터의 개수를 나타내는 정숫값 (ptr)

• ptr = 0 → 스택이 비어 있음
• ptr = N → 스택에 N개의 데이터가 있음

---

3. 스택의 구현 방식

• 리스트(List)를 이용한 스택
  • list.append(x) → push()
  • list.pop() → pop()
  • list[-1] → top()
• 컬렉션 모듈의 deque를 이용한 스택 (더 빠름)
  • deque.append(x) → push()
  • deque.pop() → pop()
  • deque[-1] → top()

---

4. 스택의 활용 예시

• 괄호 검사 ((와 ))
• DFS(깊이 우선 탐색)
• 재귀 함수의 동작 원리
• Undo/Redo 기능 구현
• 웹 브라우저의 뒤로 가기(Back) 기능

---

파이썬으로 스택 구현 예제

1. 리스트(List) 활용

stack = []

stack.append(1)   # push
stack.append(2)
stack.append(3)
print(stack.pop())  # 3
print(stack[-1])    # top() → 2

2. deque 활용 (더 빠름)

from collections import deque

stack = deque()

stack.append(1)   # push
stack.append(2)
stack.append(3)
print(stack.pop())  # 3
print(stack[-1])    # top() → 2

---

스택을 활용하여 시간 복잡도를 최적화하는 방법

스택은 push()와 pop()이 O(1) 이므로 특정 문제에서 시간 복잡도를 줄이는 데 유용함.

연산	리스트(배열)	스택(리스트)	스택(deque)
push()	O(1)	O(1)	O(1)
pop()	O(1) (마지막 원소)	O(1)	O(1)
search()	O(N)	O(N)	O(N)
top()	O(1)	O(1)	O(1)

1. 단조 증가/감소 스택을 활용한 최적화 (O(N))

각 원소의 오른쪽에서 자신보다 큰 값을 찾는 문제

• 기본적인 방법 (O(N²)) → 모든 요소를 비교
• 스택을 활용한 방법 (O(N)) → 한 번의 순회로 해결

def next_greater_element(arr):
    stack = []
    result = [-1] * len(arr)

    for i in range(len(arr)):
        while stack and arr[stack[-1]] < arr[i]:
            result[stack.pop()] = arr[i]
        stack.append(i)

    return result

arr = [3, 5, 2, 7]
print(next_greater_element(arr))
# 출력: [5, 7, 7, -1]

2. DFS (깊이 우선 탐색)에서 재귀 대신 스택 활용 (O(V+E))

재귀 DFS는 깊이가 깊어지면 스택 오버플로우 위험 존재

def dfs_stack(graph, start):
    stack = [start]
    visited = set()

    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            print(node, end=" ")
            stack.extend(graph[node])  # 인접 노드를 스택에 추가

graph = {
    1: [2, 3],
    2: [4, 5],
    3: [],
    4: [],
    5: []
}

dfs_stack(graph, 1)  # 출력: 1 3 2 5 4

3. 괄호 검사 (O(N))

올바른 괄호((), {}, []) 조합인지 확인하는 문제

def is_valid_brackets(s):
    stack = []
    mapping = {')': '(', '}': '{', ']': '['}

    for char in s:
        if char in mapping:
            top = stack.pop() if stack else '#'
            if mapping[char] != top:
                return False
        else:
            stack.append(char)

    return not stack

print(is_valid_brackets("({[]})"))  # True
print(is_valid_brackets("({[})"))   # False