[Topological Data Analysis의 기초]

본 포스팅 시리즈는 위상수학적 데이터 분석(Topological Data Analysis; TDA)의 기초 토대를 다지고자 만들어졌습니다.

TDA는 그 매력과 성과에 비해 비교적 덜 알려졌다고 생각합니다.
그래서 여러 학회에 TDA를 응용한 연구결과들을 발표할 때마다, 제한된 시간 내에 TDA의 매우 기초적인 개념부터 설명해야 한다는 점은 굉장히 저를 비롯한 TDA를 연구하는 동료들에게 고역인 일이라고 생각합니다.
본 포스팅 시리즈가 마무리되면, TDA를 짧은 시간 내에 핵심적인 아이디어만 소개할 수 있는 노하우가 생기길 기대합니다.

한편, 어쩌다 TDA를 알게되신 분들이 흥미를 가지고 TDA를 입문하고자 할 때에 입문용 자료가 많이 없어 어려움을 겪곤 하는 것을 보았습니다.
TDA에 사용되는 수학적 개념들은 평범한 수학과 학부생들도 다 익히기 어려운 개념들이 등장하곤 합니다.
특히 TDA에서 주로 사용하는 도구는 지속성 호몰로지(Persistent homology)인데, 호몰로지라는 이름부터 벌써 두려운데 거기에 지속성이라는 말까지 붙었으니, 얼마나 두려운 개념이겠습니까?
이 포스팅 시리즈를 통해 복합체(Complex), 호몰로지(Homology), 지속성 호몰로지(Persistent homology) 등의 개념을 최대한 쉽게 설명해보려 노력할 것입니다.

그러나 필자가 수학 비전공자에 대한 '공감능력' 부족으로 여전히 이해하기 어려운 설명이 있을 수 있습니다.
그런 부분에 대해 코맨트를 남겨주신다면, 정말 감사드리겠습니다.

📄 참고문헌
1. Carlsson, Gunnar. "Topology and data." Bulletin of the American Mathematical Society 46.2 (2009)
2. Zomorodian, Afra, and Gunnar Carlsson. "Computing persistent homology." Discrete & Computational Geometry 33.2 (2005)
3. Otter, Nina, et al. "A roadmap for the computation of persistent homology." EPJ Data Science 6 (2017)
4. Edelsbrunner, Herbert, and John L. Harer. "Computational topology: an introduction." American Mathematical Society, 2022.

---

3. Persistent homology

📌 핵심 Keyword

• 기하학적 추론 : 데이터들이 매니폴드로부터 얻어졌다고 가정하고, 데이터로부터 매니폴드의 기하학적 특징을 추론하는 과정.
• 지속성 호몰로지 : 필트레이션 과정에서 얻은 각각의 호몰로지가 가진 정보를 연결시켜주는 호몰로지.

§. 3.1.) Motivation

지난 포스팅에서는 하나의 심플리셜 컴플렉스에서 기하학적 특징을 추출 위해 호몰로지 개념을 도입하고 계산하는 방법을 다루었습니다.

이제 마치 문제가 다 끝난것처럼 보입니다.
그러나 중요한 이슈가 남아있습니다.

그림과 같이 6개의 데이터 포인트가 위치해있다고 합시다.
이 데이터 포인트를 심플리셜 컴플렉스로 만들고자 하면 어떻게 만들어야 할까요?

이 점들이 원형으로 배열되어 있으므로, 아래와 같이 심플리셜 컴플렉스를 구축하는 것이 타당해보인다고 주장할 수 있을 것입니다.

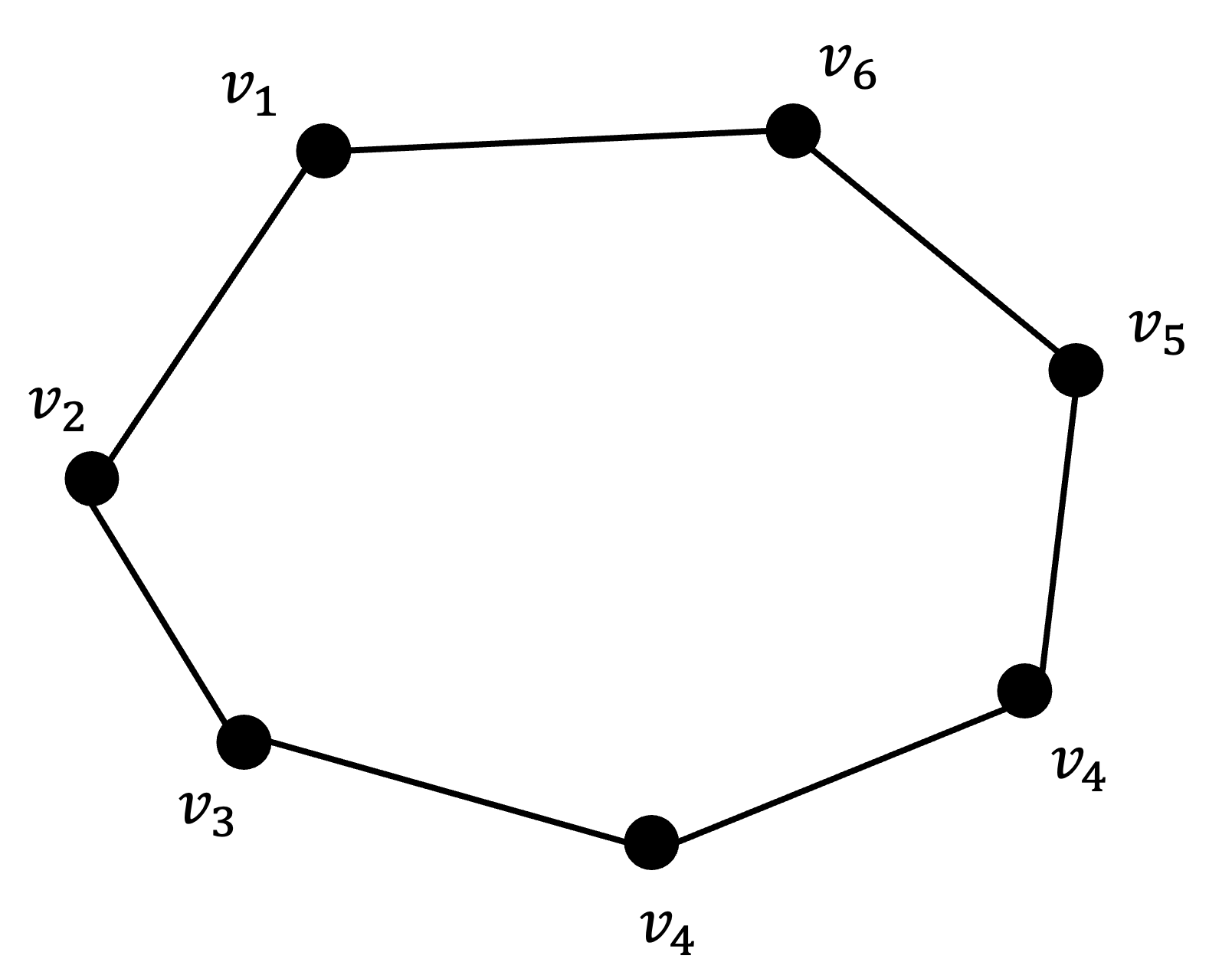
그러나 이렇게 나이브하게 점들을 연결해서 심플리셜 컴플렉스를 만드는 방식은 여러 문제점이 존재합니다.

🤔 ISSUES
1. 이러한 추론이 타당한지 보일 수 없습니다.
2. 데이터가 굉장히 크고 복잡해져서 이러한 직관이 소용이 없다면 어떤 규칙을 가지고 심플리셜 컴플렉스를 만들어야 할지 불분명합니다.
3. 수가 많고 다양한 특성을 지닌 데이터들을 일관되게 분석할 수 없습니다.

이러한 이슈들을 바탕으로 우리는 데이터에서 기하학적 특징을 추론한다는 것이 어떤 문제인지 더욱 구체화 할 수 있습니다.

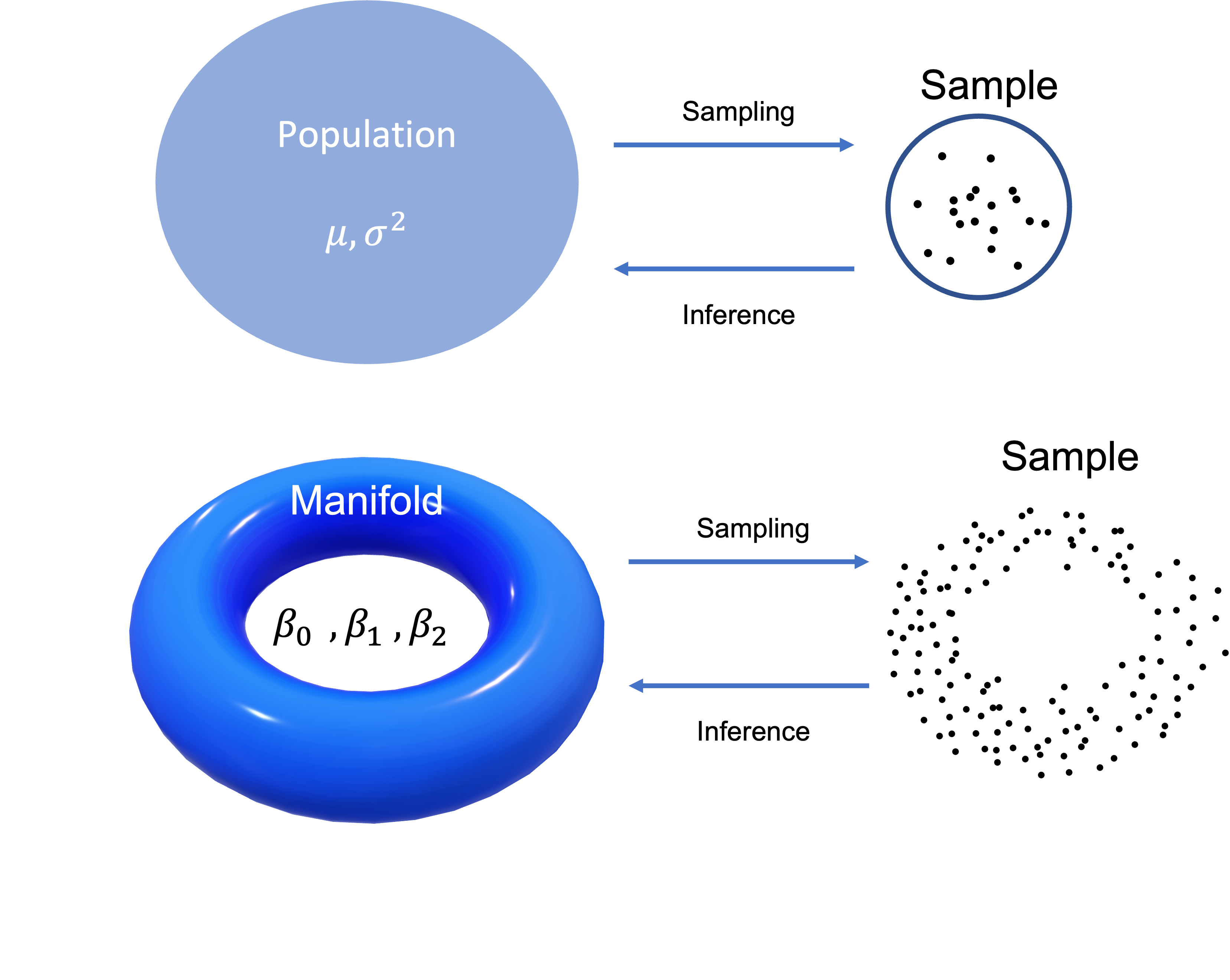
통계적 추론은 샘플된 데이터가 어떠한 분포(이를테면 정규분포)를 따르는 모집단으로부터 왔다고 가정하고 평균이나 표준편차와 같은 모집단의 분포가 가지는 특성을 합리적으로 추론하는 것이라 할 수 있습니다.

이와 유사하게 기하학적 추론은 샘플된 데이터가 어떠한 매니폴드(고차원의 기하학적 대상)으로부터 왔다고 가정하고 매니폴드가 가지는 호몰로지를 합리적으로 추론하는 것이라 할 수 있습니다.

기하학적인 관점에서 데이터들은 유클리드 공간 $\mathbb{R}^n$의 한 부분공간 $X$에서 얻어진 유한개의 점들입니다. 이를 $\mathbb{X}$로 표기합시다.
$\mathbb{X}$를 이용하여 $X$의 베티 넘버와 같은 기하학적 특징을 추론할 수 있을까요?

일반적으로 그 답은 "아니오" 입니다.
우리가 얻은 데이터엔 노이즈가 끼어 있기 때문에 부분공간 위로 온전히 놓여있을 것이라 말하기는 어렵습니다.
거기다가 이 점들을 가까이 있는 점들을 심플리셜 컴플렉스로 연결하고자 하더라도, 여전히 "얼마나 가까울 때 연결해야 하는가?" 하는 질문이 남게 됩니다.

TDA는 이 질문에 대해 다음과 같은 프로세스로 답을 제시합니다.

1. 점들을 점점 더 많이 연결시켜 가면서 심플리셜 컴플렉스를 성장시켜 나갑니다.
2. 그 과정에서 새롭게 태어나거나(born) 사라지는(die) 호몰로지의 생성원을 찾아냅니다.
3. 이때 오래 지속되는(Persist) 호몰로지의 생성원들로 매니폴드의 기하학적 정보를 추론합니다.

이 과정을 지금까지 배운 개념들로 설명해봅시다.
먼저 점들을 점점 더 많이 연결시켜 가면서 심플리셜 컴플렉스를 성장시켜나가는 과정을 필트레이션을 구축하는 것이라고 했습니다.
이에 대한 구체적인 방법으로 비에토리스-립스 필트레이션(Vietoris-Rips filtration)을 소개했었습니다.

필트레이션 $K_0 \subseteq K_1 \subseteq \cdots \subseteq K_n$을 만들고 나면, 각각의 서브 컴플렉스 $K_i$의 호몰로지를 계산하는 것으로 각각의 서브 컴플렉스가 가진 호몰로지의 생성원을 찾을 수 있습니다.
그러나 주의할 점이 있습니다.
각각의 서브 컴플렉스로부터 얻어진 호몰로지는 서로 독립적으로 구축되었기 때문에 서로 정보를 공유하지 않을 수 있습니다.
예를들어서, $K_i$에서 호몰로지 $H_1(K_i)$가 구멍이 하나 있다고 이야기해줬을 때, $K_{i+1}$에도 그 구멍이 존재하는지 아닌지 이야기해줄 수 없습니다.

오늘 다루게 될 지속성 호몰로지(Persistent homology)는 서브 컴플렉스들로부터 얻어진 각각의 독립적인 호몰로지들을 연결해줍니다.
그래서 특정 순간에 새로 발생한 호몰로지의 정보가 언제까지 지속되는지를 효과적으로 구할 수 있게 합니다.

지속성 호몰로지를 이용한 기하학적 특징의 추론은 얼마나 가까이 있는 점들을 연결시켜야 할지 걱정할 필요가 없습니다.
모든 스케일에 대해 정보를 획득하기 때문입니다.

또한 호몰로지때와 마찬가지로, 이 모든 과정은 선형대수학을 이용해 계산할 수 있습니다.
따라서 대량의 복잡한 데이터가 주어진다고 하더라도 컴퓨터를 활용해 추론을 진행할 수 있습니다.

마지막으로, 이러한 추론 과정은 꽤나 탄탄하고 깊은 이론적 근거를 가지고 있습니다.
지속성 호몰로지 이론은 카테고리 이론과 계산 위상수학 등 고급 이론들을 기반으로하고 타당성을 얻습니다.
지속성을 이용한 기하학적 추론의 철학과 자세한 이론적 배경은 TDA의 조상님이라 할 수 있는 스텐포드 Gunnar Carlsson 교수님의 유명한 논문 [Topology and data, 2009]를 참고하시길 바랍니다.

Microsoft Research에서 진행된 Gunnar Carlsson 교수님의 Topology and data에 대한 강연입니다.

---

📝 요약 Summary

• 지속성 호몰로지는 필트레이션 과정에서 얻은 각각의 호몰로지들의 정보를 연결해준다.
• 지속성 호몰로지를 이용한 기하학적 추론은 모든 스케일의 변화를 추적하기 때문에 얼마나 가까이에 있는 데이터를 연결해야하는지 고려하지 않아도 된다.
• 지속성 호몰로지를 이용한 추론은 선형대수학의 언어로 계산이 가능하기 때문에 대용량의 복잡한 데이터를 다룰 때에 효과적인 추론이 가능하다.